Математика

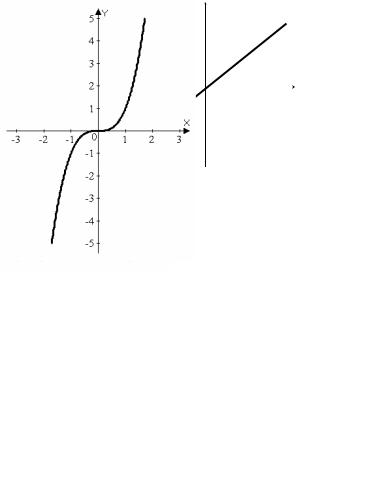
1. Степенная функция y = xα , где α – действитель-

ное число.

Приведем графики некоторых степенных функций: 1) y=х.

(α =1 )

					y
								4
				C				3
					2
-										1										x
	4	-3 -		2 -1 0				-1				1			2		3		4
								-2
									-3
									-4
2) y=x2 .					3) y=x3 .
(α = 2 )					(α = 3 )

31

4) y = 1x . (α = −1)

5) y = x . (α = 12 ).

32

2. Показательная функция y = a x , где а > 0, а ≠1.

a>1 (y=2x) 0<a<1 (y=0,5x)

3. Логарифмическая функция y= loga x , где a>0, a ≠1.

y=log2x

y= log1 x

2

33

4. Тригонометрические функции: y=sinx, y=cosx, y=tgx, y=ctgx.

5. Обратные тригонометрические функции: y=arcsinx, y=arccosx, y=arctgx, y=arcctgx.

При построении графиков функций используются сле-

дующие правила преобразования графиков:

1) График функции y=f(x)+b получается из графика функции y=f(x) путем сдвига вдоль оси Oy на b единиц

вверх при b>0 или b единиц вниз при b<0.

2) График функции y=f(x+a) получается из графика функции y=f(x) путем сдвига вдоль оси Ox на a единиц вле-

во при a>0 или a единиц вправо при а<0.

3) График функции y=kf(x) получается из графика функции y=f(x) путем растяжения вдоль оси Oy в k раз (k>1)

или сжатия в 1k раз ( 0 < k <1) . Если k<0, то к растяжению

34

(сжатию) добавляется еще симметричное отражение относительно оси Ох.

4) График функции y=f(kx) получается из графика функции y=f(x) путем сжатия вдоль оси Ox в k раз (k>1) или

растяжения в 1k раз ( 0 < k <1) .

5) График функции y=–f(x) получается из графика функции y=f(x) путем симметричного отражения относительно оси Ox, а график функции y=f(-x) получается симметричным отражением относительно оси Oy.

С помощью этих преобразований можно построить графики функций, которые получаются из основных элементарных функций путем применения рассмотренных преобразований.

Примеры

Построить графики функций:

1. y =

2x +1

.

x −1

Решение

Преобразуем

функцию

следующим

образом

y =

2x +1 =

2x − 2 + 3 =

3

+ 2 . График этой функции

x −1

x −1

x −1

3

получается из графика функции

y =

путем его сдвига

x

на 1 единицу вправо вдоль оси Ох (см.п.2,

a

= 1 ) и

сдвигом полученного графика вверх вдоль оси Оy на 2 единицы вверх.

35

Рис. 4.

2. y = sin 2x .

Решение

Строим график функции y = sin x , далее сжимаем

график по оси абсцисс в два раза, то есть уменьшаем абсциссы точек графика в два раза, оставляя ординаты без изменения. При этом, заметим, что период функции y = sin 2x равен π . Сжатие графика функции удобно про-

	водить в		характерных точках графика функции
	y = sin x ( 0,	π	,π,	3π	, 2π и т.п., где π = 3,14 )
		2		2

36

Рис.5

3. y = sin2 x .

Решение

Прежде чем строить график, преобразуем данную функцию к виду y = − 12 cos 2x + 12 . График этой функции

получим из графика функции y = cos x , выполнив последо-

вательно такие преобразования: сжатие по оси абсцисс в два раза; сжатие по оси ординат в два раза; симметричное отображение относительно оси абсцисс; параллельный перенос

вдоль оси ординат вверх на 12 единицы масштаба. График функции y = sin2 x представлен на рис. 6.

Рис.6

37

Пример

Решить графически уравнение 4x-4+х=0.

Решение

Перепишем уравнение в виде 4x=4–х. Корнем этого уравнения будет значение x = x0 , подстановка которого об-

ращает уравнение в верное числовое равенство: 4x0 = 4 − x0 . Геометрически x0 –это абсцисса общей точки( точек) графиков функций y1 = 4x и y2 = 4 − x . Построим в системе координат графики функций y1 и y2 . Для этого найдем контрольные точки:

1.f (x) = 4x : x=0, y=1; x=1, y=4.

2.g(x) = 4 − x : x=0, y=4; x=1, y=3.

y=4x

y=4–x

Рис.7

38

Точка пересечения этих кривых имеет абсциссу x0 ≈0,8. Значит, данное уравнение имеет единственный ко-

рень x0 ≈ 0,8.

2. Предел функции

Пусть дана функция y=f(x). Если значения функции f(x) неограниченно приближаются к некоторому числу А, когда значения аргумента х неограниченно приближаются к а , при этом x ≠ a , то число А называется пределом функции f(x) при стремлении х к а. Кратко это записывается так :

lim f ( x ) = A .

x→a

	Пример
	Пусть дана функция	y =	x2	−1		. Найдем предел этой
			x	−1

функции при х, стремящемся к 1. Рассмотрим несколько значений аргумента, близкие к 1, и соответствующие им значения функции:

X	0	2	0,5	1,4	0,8	1,1	0,9	0,99	1,001
Y	1	3	1,5	2,4	1,8	2,1	1,9	1,99	2,001

Можно заметить, что при неограниченном приближении х к единице, значения функции неограниченно прибли-

жаются к 2. Значит

lim

x2

−1

= 2 . Этот же результат можно

x

−1

x→1

x →1, но

x ≠1,

получить, преобразовав функцию: так как

то

x −

1 ≠ 0 и

x2 −1

=

(x −1)(x +1)

= x +1.

Тогда

x −1

(x −1)

lim

x2 −1

= lim(x +1)= 2 .

x −1

x→1

x→1

39

Если lim f ( x ) = 0 , то функция f(x) называется беско-

x→a

нечно малой при x → a . Например, функция f ( x ) = (x −1)2 при x →1 бесконечно малая величина, так как

lim(x −1)2 = 0 .

x→1

Если при x → a абсолютные значения функции неограниченно возрастают, то функция называется бесконечно большой приx → a . Это записывается так: lim f ( x ) = ∞.

											x→a
Например,		lim		1				= +∞ .
					2 )2
		x→2 ( x −
	Аналогичные ситуации могут возникнуть при неогра-
ниченном		увеличении							х (по	модулю).	Например,
lim	5x + 2	= lim		5	+	2			= 5.
	x					x
x→∞		x→∞									х значения
	Если	при неограниченном								увеличении

функции неограниченно возрастают, то функция называется

бесконечно		большой		при		x → ∞ .		Например,
lim(x2 + 2x)= +∞.
x→∞	При нахождении пределов используются следующие
теоремы о пределах:
1.	Если lim f ( x ) = A ,		lim g( x ) = B , то
	x→a		x→a
lim( f ( x ) ± g( x )) = A ± B , lim( f ( x ) g( x )) = A B ,
x→a			x→a
lim c f ( x ) = c lim f ( x ) , lim				f ( x )	=	A	, при условии, что
x→a		x→a	x→a	g( x ) B

lim g( x ) ≠ 0 .

x→a

Замечание: теоремы о пределах справедливы и при x → ∞ .

40