Математика

sin 4x

104.

lim

4x4

−8x

;

3x

4 −

5x2 + 6

x→∞

lim

x2

− x −12

;

x2 −9

x→−3

105.

lim

x4 + 2x2 −3

;

5x4 −3x + 2

x→∞

lim

2x

2 − x −1

;

x2

−3x +

2

x→1

106.

lim

x2 − 4

;

3x2 − x −

10

x→2

lim

x

−1

2 x

;

+1

x→∞ x

107.

lim

x2 − 2x

;

x2

− 4x + 4

x→2

lim

x

− 3

4 x

;

x

x→∞

108.

lim

x2 + x

;

x2 − x − 2

x→−1

lim x3 3+ x2 +1 ;

x→∞ 4x + x −1

x −1					x
lim					;
			x
x→∞
lim			x tg x			.
			− cos 5x
x→0 1

x

lim x +1 3 ; x→∞ x − 2

lim sin 3x cos 2x .

x→0

lim 18x3 −3x2 +1 ; x→∞ x2 + x −6x3

lim sin 5x + sin 3x .

x→0 4x

lim			sin 7x					;
	tg (x			+π)
x→0
lim			3x5 + 4x3 + 6							.
x→∞ 2x5 + x4 + 7x −1
lim	1 − cos x					;
x→0			x tg 2x
lim	x +			9	x
					.
x→∞ x +8

51

109.

lim

x

2

+ 3x

;

lim

1 − cos 5x

;

sin

2

2x

x3 + 27

x→−3

x→0

lim

x

3

+12x

4

+ 3x

2

;

x +1

x

3

x→∞

1 + x4 + x2

lim

.

x→∞ x − 2

110.

lim

2x sin 3x

;

x +1

x+2

1 − cos 6x

lim

;

x→0

x→∞ x + 3

lim

x3

− x2 +1

;

lim

x2 + x −6

.

4x3 + 3x2

x3 −8

x→∞

x→2

111-120. Исследовать функцию y = f (x) на непрерывность.

Построить схематично график функции. Указать характер точек разрыва.

111.

112.

113.

114.

115.

52

1

y = 5 − 4 x ;

1

y = 3x + 2 ;

1

y = 4(x−1)2 ;

1

y = 2 x+1 +1 ;

1

y = 5(x−3)2 +1 ;

x,				x ≤ −1		.
y =	− x2 ,			x > −1
4
y = 2x ,			x ≤ 0 .
x2 +1, x > 0
	x	,		x <1 .
y = 3
x2 ,				x ≥1
4 − x,			x < 2		.
y =	2 − 4, x ≥ 2
x
		2		, x ≤1
(x − 2)						.
y =
	x	+1,		x >1
2

1	− 3 + x, x ≤ −3

116.

y = 4

x−1

+ 2 ;

y = 9 − x2

, x > −3 .

1

x

+1,

x < −2 .

117.

y = 2 x

+1 ;

y = 3

4 + x2 , x ≥ −2

1

2

≤1.

118.

y = 5x2

−3;

y = 1

− (x +1) , x

2 − x,

x >1

1

x

,

x ≤ 0 .

119.

y =1 − 4 x−2 ;

y = 2

x2 − 2x, x > 0

1

sin x +1, x ≤ 0

120.

y = 3

(x−2)2

;

y =

x > 0

.

− x,

53

III. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

И ЕГО ПРИЛОЖЕНИЯ

1.Производная

Пусть функция y=f(x) определена в точке х0 и в некоторой окрестности этой точки. Рассмотрим два значения ее аргумента: исходное х0 и новое значение х. Приращением аргумента в точке х0 называют разность x = x − x0 , отку-

да x = x0 + x . Аналогично разность f ( x ) − f ( x0 ) назы-

вется	приращением			функции		f(x)	и	обозначается		y :
y = f (x0 +		x) − f (x0 ) . Отсюда				f ( x0 +		x ) = f ( x0 ) +		y .
Определение. Производной функции								y = f ( x ) в точке
x0 называется предел отношения приращения функции										y
в этой точке к вызвавшему его приращению аргумента										x
при условии,		что x		произвольным образом стремится к
нулю. Производная функции f(x)						в точке		x0 обозначается
f ′(x0 ) .	Итак, по определению
f ′(x0 ) =		= lim	y	= lim	f (x0	+	x) − f (x0 )		.
			x
		x→0		x→0			x

Определение. Функция y = f ( x ) , имеющая в точке х0

производную, называется дифференцируемой в этой точке. Операция нахождения производной функции называется дифференцированием этой функции. Для одной и той же функции y = f ( x ) производная в различных точках х

может принимать различные значения, то есть в свою очередь является функцией от х.

Выясним геометрический смысл производной. С этой целью введем определение касательной к кривой в данной точке. Пусть на кривой L выбрана точка М0 . Рассмотрим другую точку М кривой, и проведем секущую М0М.

54

Определение. Касательной к кривой L в точке М0 на-

зывается предельное положение секущей М0М , когда точка М , перемещаясь по кривой L, неограниченно приближается к точке М0 (рис. 10).

M секущая

касательная

Mo

L

Рис. 10.

Рассмотрим график непрерывной функции y = f ( x ) , имеющей в точке М0 с абсциссой x0 невертикальную касательную (рис. 11). Дадим x0 приращение x . По чертежу видно, что x = M 0 P . Тогда функция получит приращение y = MP .

	Точка	М	графика		функции имеет координаты
	М( x0 + x; y0	+	y ). Пусть секущая М0М образует с осью
	ОХ угол ϕ . Тогда tgϕ =				MP	=	y . При стремлении x к
				M 0 P
						y	x
	нулю приращение функции						также стремится к нулю, и

точка M , перемещаясь по графику функции, неограниченно приближается к точке M 0 . При этом секущая M 0 M , по-

ворачиваясь около точки M 0 , стремится занять положение

55

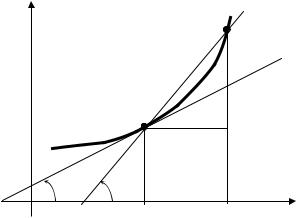
M 0 T – касательной к графику функции y = f ( x ) в точке

M 0 ( x0 ; f ( x0 )) . Поэтому
kкас = tgα = lim tgϕ = lim				y	=	′		).
				x		f ( x0
		x→0	x→0
								секущая
	y
						M

касательная

	T
Mo	P

		α		ϕ
								x
0						xo	xo+ x

Рис. 11.

Значит, значение производной функции y = f ( x ) в точке x0 равно угловому коэффициенту касательной к графику функции y = f ( x ) в точке M 0 . Используя уравнение прямой, проходящей через точку M 0 с заданным угловым коэффициентом y − y0 = k( x − x0 ) , можно написать урав-

нение касательной к графику функции y=f(x) в точке х0 . Оно будет иметь вид y − f ( x0 ) = f ′( x0 )( x − x0 ) .

Отметим также механический смысл производной. Пусть материальная точка движется по прямой по законуs = s( t ) . Тогда производная s(t) по t характеризует ско-

рость точки в момент времени t v(t) = s′(t) . Эту скорость называют иногда мгновенной скоростью точки.

56

	Приращение			y = f (x0 +			x) − f (x0 )		иногда удобно
заменять		приближенной величиной						′	)( x − x0 ). Гео-
								f ( x0
метрически это равносильно замене дуги M 0 M на участке
графика функции отрезком прямой								M 0T :	y ≈	′
										f ( x0 ) x .
		′		x ,	линейное относительно					x , называ-
Выражение f ( x0 )
ется	дифференциалом функции						y = f ( x )		и обозначается
dy .	Значит,		dy =		′	x .	Пусть		y = x ,		тогда
					f ( x0 )
		′	x =	x ,	то есть		dx =	x . Поэтому оконча-
dy = dx = ( x )
тельно		имеем			dy =	′			Геометрически
						f ( x0 )dx .
dy =	x tgα = PT . Отрезок					PT	выражает приращение ор-
динаты касательной при переходе от								x0 к	x0 +	x .	Таким
образом, дифференциал функции y = f ( x ) в точке х0											равен

приращению ординаты касательной, проведенной в точке с абсциссой x0 . Окончательно имеем: dy = f ′( x )dx . Отсюда

в частности вытекает, что производную можно рассматри-

вать, как отношение дифференциалов dy и dx : f ′( x ) = dydx .

Приведем таблицу производных основных элементарных функций.

Основные формулы дифференцирования:

1.

c

′

= 0 ;

2. ( x

n ′

n−1

; 3. (e

x

)

′

= e

x

;

) = nx

4.

(a x )′ = a x ln a ;

5.

(ln x)′ =

1

;

6. (loga

x)′ =

1

;

x ln a

x

7.

(sin x)′ = cos x ;

9.

(cos x)′ = −sin x ; 10.

(tgx)′ =

1

;

cos2 x

1

′

1

11. (ctgx) = −sin 2

x ; 12.

1 − x2

;

(arcsin x ) =

13. (arccos x )′ = −

1

; 14. ( arctgx )′ =

1

;

1 − x2

1 + x2

57

15. (arcctgx)′ = −1 +1x2 .

Если u = u( x ) и v = v( x ) – дифференцируемые функции,

то справедливы следующие правила.

Основные правила дифференцирования:

1.(u ± v)′ = u′± v′.

2.(u v)′ = u′v +u v′.

3.( cu ) = cu′. .

4.u ′ = u′v −v′u .v v2

Дадим определение сложной функции. Пусть функция y=f(u) определена на множестве D, а функция u=g(x) на множестве D1 , причем любому х D1 соответствует значе-

ние u=g (x), где u D . Тогда на множестве D1 определена

функция y=f(g(x)), которая называется сложной функцией от x. Производная этой функции будет определяться по формуле

y′x = fu′ u′x .

То есть производная сложной функции равна производной внешней функции f (u) , вычисленной в точке

u = g(x) , умноженной на производную внутренней функции g(x) в точке х.

Примеры

1. Тело движется по закону s( t ) = 4 +8t + 5t2 . Найти

скорость тела в начальный момент времени (t=0) и через t=6 сек.

Решение

Найдем скорость тела в произвольный момент времени t. v( t ) = s′( t ) = 8 +10t . Теперь вычислим значение этой ско-

рости в конкретные моменты времени. 58

v( 0 ) = 8 +10 0 = 8 ; v( 6 ) = 8 +10 6 = 68 .

2.

Найти производные:

1) y = ( x2 + 3x )3 .

Здесь y = u3 , где u = x2 + 3x . Тогда

y

′

= 3u

2

u

′

= 3( x

2

+ 3

x

)

2

( x

2

+ 3

x ′

) =

= 3( x2 + 3x )( 2x + 3x ln 3).

2)

y =

cos3

x −1

. Производная равна

1 − x2

2

2

3

1 ( −2x )

3cos

x( −sin x ) 1 − x

−(cos

2

x −1)

2 1 − x

y′ =

.

1

− x2

3. Дана функция y= x2

− 6x +8 . Найти координаты то-

чек пересечения графика этой функции с осями координат. Построить график функции. Написать уравнение касательной к графику функции в точке с абсциссой x0 = 4 . По-

строить касательную на чертеже.

Решение

Найдем точки пересечения графика с осями координат: x = 0; y = 8. То есть точка пересечения с осью OY

имеет координаты M ( 0;8 ) . Для нахождения абсцисс точек

пересечения с осью OX решим уравнение: x2 − 6x +8 = 0 . Получим: x1 = 2; x2 = 4 . Таким образом, точки пересечения с осью OX будут M1( 2;0 ) и M 2 ( 4;0 ) . Для определения координат вершины O1 параболы выделим полный квадрат

y = ( x2 − 2 x 3 + 9 ) −1 = ( x − 3)2 −1. ТогдаO1( 3;−1) .

Составим уравнение касательной в точке (4;0).

59

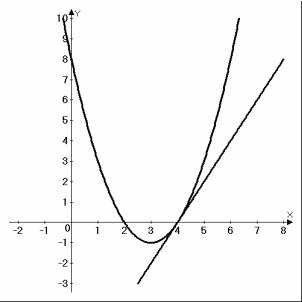
y′ = 2x −6 . y′( 4 ) = 2 . Уравнение касательной будет y − 0 = 2( x − 4 ) или y = 2x −8 . Изобразим параболу и касательную к ней на чертеже (рис. 12).

Рис. 12.

2. Производные высших порядков

Производная y′ = f ′(x) функции y=f(x) есть также

функция от х и называется производной первого порядка.

Производные порядка выше первого называются производными высших порядков. Если функция f ′(x) дифференци-

руема, то ее производная называется производной второго порядка и обозначается y′′ = ( y′)′. Производной n-ого по-

рядка называется производная от производной (n-1) поряд-

ка y(n) = ( y(n−1) )′.

60