Математика

			Пример
			Найти производную второго порядка							функции
y =			x			.
			cos x
			Решение
			y′ = cos x + x sin x					. Тогда
							cos2 x
y	′′	= ( y		′ ′		=	( x cos x )cos	2 x − 2 cos x(	−sin x )(cos x + x sin x )		.
				)				cos4	x

3.Производные функций, заданных параметрически

Пусть зависимость между аргументом х функцией y

x = x(t)	, где
задана параметрически в виде двух уравнений
y = y(t)

t – вспомогательная переменная, называемая параметром. Причем, в некоторой области изменения параметра t функ-

ции	x( t ) и y( t )			дифференцируемы и			′
							x ( t ) ≠ 0 . Найдем
производную y′x .				Так как производная равна отношению
дифференциалов y и x, то y′x = dy					=	yt′dt	=	yt′	. Таким обра-
						xt′dt
		yt′		dx				xt′
зом,	y′x =		.
		xt′
	Пример
	Пусть x = t 3			. Найти y′x .
		y = t sin t

Решение

Имеем xt′ = 3t 2 , yt′ = sin t +t cost .Тогда

61

y′x =	sin t + t cos t	.
	3t2

4.Вычисление пределов по правилу Лопиталя

Рассмотрим метод раскрытия неопределенностей вида

0 и ∞ , который основан на применении производной.

∞0

Теорема. Пусть функции y=f(x) и y =ϕ(x) непрерывны и дифференцируемы в окрестности точкиx0 и обращаются в

ноль в этой точке: f (x0 ) =ϕ(x0 ) = 0 . Пусть ϕ′(x) ≠ 0 в некоторой окрестности этой точки. Если существует предел отношения производных этих функций, то он равен пределу

отношения самих функций lim			f (x)		= lim		f ′(x)	.
		x→x0	ϕ(x)			x→x0	ϕ (x)
							′
Это	правило	справедливо				также			и	если
lim f (x) = lim ϕ(x) = ∞.		Тогда оно дает возможность рас-
x→x0	x→x0
крывать	неопределенности вида					∞	Если		отношение
						.
						∞

производных опять представляет собой неопределенность

0		или		∞	, то можно правило Лопиталя применить по-
0				∞

вторно, то есть перейти к пределу отношения вторых производных.

	Примеры
	Вычислить пределы.					′
		x −1		0
	1. lim		=		= lim		= lim
		x ln x				′
				0
	x→1				x→1		x→1

1			=
ln x + x	1
	x

62

= lim		1		=1.
x→1 ln x +1
2. lim		ln sin 2x			=		∞	=
		ln sin x
x→0							∞

2соs2x

= lim 2 cos 2x sin x

= lim

sin 2x

=

x→0

cos x

x→0

cos x sin 2x

sin x

= lim

2 cos 2x sin x

= lim cos 2x

=1.

x→0

2 sin x cos2 x

x→0 cos2 x

1

sin

1

0

{∞ 0}= lim

x

3. lim x sin

=

=

=

x

1

x→∞

x→∞

0

1

1

x

(cos

)(

)

−

1

) =1 .

= lim

x

x2

= lim(cos

1

x→∞

x→∞

x

( −

)

x2

x −1 − ln x

1

1

4. lim

−

= {∞ − ∞}= lim

x −1

(ln x )( x −1)

x→1 ln x

x→1

1 −

1

0

1

1

= lim

x

2

x

=

= lim

=

.

x −1

1

1

x→1

+ ln x

0

x→1

+

2

x

x2

x

=0 =0

5.Исследование функций и построение графиков

Важное применение производная находит при построении графиков функций. Введем некоторые понятия.

Функция y=f(x) называется строго возрастающей на интервале (a; b), если для любых x1 , x2 (a, b) таких, что

63

x1 < x2 , справедливо f (x1 ) < f (x2 ) ( если f (x1 ) > f (x2 ) , то функция строго убывает).

Интервал, на котором функция строго убывает или возрастает, называется интервалом монотонности функции. Причем, если f ′(x) > 0 на интервале, то функция стро-

го возрастает; если f ′(x) < 0 – строго убывает.

Если в точке x0 производная функции равна нулю или

не существует, то эта точка называется критической. Критическими являются все точки экстремума (точки максимума и минимума). Точка x0 называется точкой максимума,

если существует такая окрестность этой точки, что для всех х из этой окрестности, отличных от x0 , справедливо нера-

венство f (x) < f (x0 ) . Если f (x) > f (x0 ) , то x0 – точка минимума. При переходе через точку максимума знак первой производной меняется с плюса на минус, а через точку минимума – с минуса на плюс.

Интервалы выпуклости и вогнутости графика функции определяются с помощью второй производной. Если на интервале f ′′(x) > 0 , то график функции на этом интервале –

выпуклый вниз (вогнутый), если f ′′(x) < 0 – выпуклый

вверх (выпуклый). Точкой перегиба называется точка, при переходе через которую, график функции меняет направление выпуклости. В этих точках вторая производная равна нулю или не существует.

Построение графика функции значительно упрощается, если найти его асимптоты. Прямая называется асимптотой графика функции y=f(x), если расстояние от точки, удаляющейся по графику в бесконечность, до этой прямой стремится к нулю. Асимптоты могут быть вертикальными, наклонными и горизонтальными.

64

Прямая х=а является вертикальной асимптотой гра-

фика функции y=f(x) , если lim f ( x ) = ∞, или бесконечно-

x→a

сти равен один из односторонних пределов.

Уравнение наклонной асимптоты графика функции

	y=f(x)	имеет вид y=kx+b, где k = lim	f ( x )	и
			x
		x→∞

b = lim( f ( x ) − kx ) . Если к=0 и b = lim f ( x ) существует, то

x→∞ x→∞

уравнение y=b определяет горизонтальную асимптоту. Приведем план полного исследования функции с по-

мощью производной:

1.Найти область определения функции;

2.Найти точки пересечения графика с осями координат, нули функции и интервалы знакопостоянства; четность, нечетность;

3.Найти асимптоты графика функции; исследовать поведение функции в точках разрыва;

4.Найти критические точки и исследовать функцию на монотонность;

5.Найти точки перегиба и промежутки выпуклости.

Примеры

1. Построить график функции y = (x +1)3 −3x −3 . Найти наибольшее и наименьшее значения функции на отрезке [− 4; 1].

Решение

1.Область определения функции – вся числовая ось, то есть D( f ) : (− ∞;+∞).

2.Точки пересечения графика с координатными осями будут: с осью Oy – (0;-2); с осью Ox :y=0, тогда

( x +1)( x2 + 2x +1 − 3) = 0 ,

( x +1)( x2 + 2x − 2 ) = 0 при х=-1, х≈ -2,7, х≈0,7.

65

3. График функции асимптот не имеет, так как

	k = lim	f ( x )	= ∞ .
		x
	x→∞
	4.	Найдем критические точки:

y′ = 3( x +1)2 − 3 = 3( x2 + 2x ) Производная равна ну-

лю при х=0 и х=-2. Результаты исследования функции на монотонность сведем в таблицу

x

( −∞, − 2 )

-2

(-2; 0)

0

( 0, + ∞)

y′

+

0

–

0

+

y

↑

2

↓

-2

↑

Таким

образом, x = −2

–

точка

максимума,

ymax

= y( −2 ) = 2 ,

точка

х=0

–

точка

минимума,

ymin

= y( 0 ) = −2 .

5. Исследуем график функции на выпуклость и вогну-

тость. Найдем y′′: y′′ = 3( 2x + 2 ) .

3( 2x + 2 ) = 0 при х= –1. Результаты исследования от-

разим в таблице

x

( −∞, −1)

-1

( −1, + ∞)

y′′

–

0

+

y

∩

0 Т.п.

Точка с абсциссой х=–1 – точка перегиба.

6.Строим график функции (рис.13).

7. Найдем наименьшее и наибольшее значения функ-

ции отрезке

[− 4;1]. Для этого найдем значение функции на

концах отрезка:

y( −4 ) =-18; y(1)=2. Сравним их со значе-

ниями

функции

в

точках

максимума

и

минимума:

y( −2 ) = 2 и

y( 0 ) = 2 (точки

x=–2 и x=0

попадают в дан-

ный

отрезок).

Тогда

yнаиб

= y(1) = y( −2 ) = 2

и

yнаим = y( −4 ) = −18 .

66

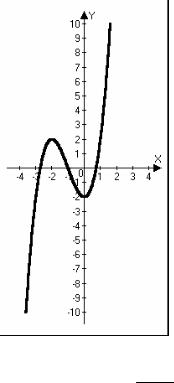
Рис. 13

2. Построить график функции y = 1−xx2 .

Решение

1. Знаменатель дроби обращается в ноль при x = ±1, поэтому область определения будет иметь вид

(− ∞;−1) (−1;1) (1;+∞).

2. Так как y=0 при x=0, то график функции проходит через начало координат. Функция принимает положительные значения в интервалах (− ∞;−1) и (0;1), и отрицатель-

ные значения в интервалах (−1;0) и (1;+∞).

67

Функция

является

нечетной,

так

как

y( −x ) =

− x

= −y( x ) .

Следовательно,

график

функ-

1 −( −x )2

ции симметричен относительно начала координат.

3.

Так как

lim

x

= m∞ и lim

x

= m∞, то

1 − x2

− x2

x→−1±0

x→1±0 1

прямые x=1, x=-1 являются вертикальными асимптотами.

Выясним				наличие	наклонных					асимптот:
lim		x		= 0 . Тогда b = lim(				x	−0 x ) = 0 . Следо-
		− x2 )x				1		− x2
x→∞ (1				x→∞

вательно, прямая y=0 (ось Ox) является горизонтальной

асимптотой.
4.		Найдем интервалы возрастания и убывания.
		x	′	x2 +1		y′ > 0 при любом х из об-
y′ =			=		. Так как,
				(1 − x2 )2
1 − x2

ласти определения функции, то функция не имеет экстремумов и монотонно возрастает в каждом из интервалов

(− ∞;−1) (−1;1) (1;+∞).

5. Найдем интервалы выпуклости и точку перегиба.

	x	2	+1				′		2x( x	2	+ 3)
y′′ =								=						.
				2
	(1 − x				)	2			(1 − x		2	)	3

Вторая производная равна нулю при х=0.

Результаты исследования графика на выпуклость и вогнутость занесем в таблицу

x	( −∞, −1)	-1	(-1 ;0)	0	(0; 1)	1	(1;+∞)
у"	+	Не сущ	–	0	+	Не	–
						сущ.
y		Не сущ	∩	0		Не	∩
						сущ.

Точка с координатами О(0;0) – точка перегиба.

68

6. На основании результатов исследования строим график функции y = 1 −xx2 (рис. 14).

Рис.14

69

Задания для контрольной работы №3

121-130. Найти производные функций.

121.

y =

ln x

;

y = e

3x

tg 3x ;

2

y = (x

2

+ cos 2x) .

x2 +1

122.

y =

tg x

;

y = (1− x2 ) arctg x ; y = sin2 (2x +1).

x3 + x

123.

y =

1 − x2

;

y = ex2

arcsin x ;

y = tg 2 (x + x3 ).

x

124.

y =

4 − x2

y = 24 x arctg x ;

y = cos2 (x2 −1)

x − 4 ;

125.

y =

ln(x +1)

y = 42 x 4 −5x ;

y = arctg 2 (2x +1).

cos 2x

126.

3

x + 4

y = 2

3x

arccos x ;

2

3x 3

y = tg x ;

y = (x + e ) .

127.

y =

cos 3x

;

y = tg x ln cos x ;

y = arcsin2 (x +1).

3

2x − 4

128.

y =

cos 3x

;

y = 2x2

arctg x ;

y = cos4 4x +1.

x3 −

x

129.

x2

+1

y = ln2

x e−3x ;

y = arctg

(3x + e2 x )

y = ctg 2x

;

130.

y =

x − x2

;

y = 2x−4 ctg x ;

y = (ln sin x + 4)3 .

sin 3x

70