Березкин Основы теории информации и кодирования 2010

j( 1 ) .

S2 ( j ) e j t0 x1 ( )e j d e j t0 S1 ( j ) S1 ( )e j ( 1 t0 ) .

Сдвиг во времени функции x(t) на величину t0 приводит к изменению фазовой характеристики спектра S( j ) на величинуt0 . Модуль S( ) от положения колебания на оси времени не зависит.

2.3.2. Инверсия сигнала

Пусть колебание x1 (t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1 ( j ) . При инверсии этого колебания (при сохранении его формы) получим новую функцию времени x2 (t) x1(t) , существующую на интервале от t1 до t2 (рис. 2.5).

Спектральная плотность колебания x2 (t) имеет вид

S2 ( j ) x2 (t)e j t dt x1 (t)e j t dt S1 ( j ) .

	x(t)	x1 (t)
		S1 ( j )
		t
		2
		)
		S2 ( j )
		Рис. 2.5. Инверсия сигнала

Учитывая, что 1 e j cos j sin , спектральную плотность S2 ( j ) можно представить в виде S2 ( j ) S1 ( )e

Итак, инверсия сигнала x1(t) приводит к изменению фазовой характеристики спектра S1 ( j ) на величину .

51

2.3.3. Изменение масштаба времени

Пусть колебание x1 (t) подверглось сжатию во времени. Новое сжатое колебание x2 (t) связано с исходным колебанием соотношением x2 (t) x1(nt), n 1 (рис. 2.6).

x(t)

)

t

/n

Рис. 2.6. Сжатие сигнала

Спектральная	плотность колебания	x2 (t)	имеет вид

S2 ( j ) x2 (t)e j t dt x1 (nt)e j t dt . Вводя новую перемен-

		( j ) 1			d . Но полученный
ную nt , получаем S	2			x ( )e j n
		n		1

интеграл есть не что иное, как спектральная плотность исходного колебания x1 (t) при частоте n , т.е. S1( j n ) . Таким образом,

S2 ( j ) 1n S1 ( j n ) .

Итак, при сжатии колебания в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в n раз. Очевидно,

что при растягивании колебания ( n 1 ) имеет место сужение спектра и увеличение модуля.

2.3.4. Сдвиг спектра колебания по частоте

Применим преобразование Фурье к произведению следующего

52

вида x2 (t) x1(t) cos 0t :

			1				1
S2 ( j ) x1 (t) cos 0te j t dt x1				e j		0t		e
		(t)	2				2		j		0t	e j t dt
1	x (t)e j ( 0 )t dt	1 x (t)e j ( 0 )t dt .
2	1	2	1

Первый интеграл в правой части есть не что иное, как спектральная плотность функции x1 (t) при частоте 0 , а второй инте-

грал – при 0 .
Таким образом, S2 ( j )	1	S1 j( 0 ) S1 j( 0 ) . Рас-
	2

щепление спектра S1( j ) на две части, смещенные соответственно на 0 и 0 , эквивалентно умножению функции x1 (t) на гармоническое колебание cos 0t .

2.3.5. Сложение колебаний

Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным преобразованием, то очевидно, что при сложении колебаний x1 (t), x2 (t),... , обладающих спектрами S1 ( j ), S2 ( j ),..., суммар-

ному колебанию x(t) x1 (t) x2 (t) ... соответствует спектр

S( j ) S1 ( j ) S2 ( j ) ....

2.3.6. Дифференцирование и интегрирование колебания

Дифференцирование (интегрирование) колебания x1 (t) можно

рассматривать как почленное дифференцирование (интегрирование) всех гармонических составляющих, входящих в его спектр.

Гармоническую составляющую колебания			x1 (t)	при частоте
можно представить в следующем виде:	1				j t	. Заклю-
			S ( j )d e
			1
	2

ченная в квадратные скобки величина представляет собой ампли-

53

туду колебания в полосе d . Следовательно,

колебанию

x2 (t)

dx1 (t)

соответствует

спектральная

плотность

dt

1

S2 ( j ) j S1 ( j ) , а x2 (t) x1

(t)dt – S2 ( j )

S1 ( j ) .

j

L

2.3.7. Произведение колебаний

Пусть рассматриваемое колебание x(t)

является произведением

двух функций времени x(t) f (t)g(t) .

Определим спектр колебания x(t) :

S( j ) x(t)e j t dt f (t)g(t)e j t dt .

Каждую из функций

f (t) и

g(t) можно представить в виде

интеграла Фурье

1

1

f (t)

F ( j )e j t d , g(t)

G( j )e j t d .

2

2

Подставляя второй из них в S( j ) , получаем

1

j t

j t

S( j )

f (t)

G( j )e

d e

dt

2

1

j ( )t

G( j ) f

(t)e

dt d .

2

Заключенный в квадратные скобки интеграл представляет собой

	спектральную плотность функции				f (t) при частоте			, т.е.
	F j( ) . Следовательно,				1
				S( j )		G( j )F j( ) d .
					2
							f (t) и g(t) равен (с
	Итак, спектр произведения двух функций
	коэффициентом	1	)	свертке			их	спектров
		2
				54

x(t)

S( j ) 21 G( j ) * F ( j ) .

2.3.8. Взаимная заменяемость и t в преобразовании Фурье

Для четной функции x(t) можно произвольно выбирать знак перед t в обратном преобразовании Фурье. Выберем знак минус и

1

запишем формулу в виде x(t) 2 S ( j )e j t d . Произведем теперь в последнем интеграле замену переменной интегрирования

на t и параметра t на . Тогда x( ) 1 S ( jt)e j t dt . Но

2

этот интеграл можно рассматривать как спектральную плотность новой функции S( jt) , полученной путем замены на t в выра-

жении спектральной плотности колебания .

Обозначим эту новую спектральную плотность через S ' ( j ) . Тогда S ' ( j ) 2 x( ) .

Итак,	переменные и t	в преобразовании Фурье взаимно за-
менимы:	если четному колебанию x(t) соответствует спектр
S( j ) , то колебанию S( jt)		соответствует спектр 2 x( ) .

2.4. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ОДИНОЧНОГО ПРЯМОУГОЛЬНОГО ИМПУЛЬСА

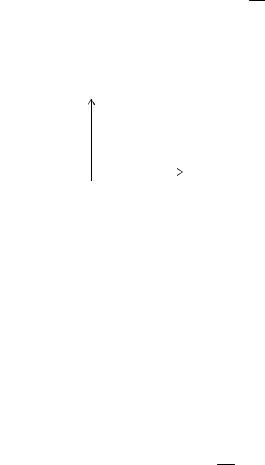
Простейшее колебание (рис. 2.7), определяемое выражением

	h,			t					;
			2					2
	x(t)
	0,				t				,
								2

получило широкое распространение как в технике, так и в теории сигналов.

Применяя преобразование (2.4), находим

55

S( j )

/ 2

j

2

x(t)e

j t

dt

h e

j t

dt

h

e

e

/ 2

j

2h sin

h sinc

e j ( ) .

h

sinc

2

2

2

x(t)

h

t

-

j

2

Рис. 2.7. Одиночный прямоугольный импульс

Заметим, что произведение h , равное площади импульса, определяет значение спектральной плотности импульса при 0 , т.е. S(0) h . Этот вывод можно распространить на импульс про-

извольной формы. Таким образом	S( j ) S(0)sinс
			2 .

При удлинении (растягивании) импульса расстояние между нулями функции S( j ) сокращается, что равносильно сужению

спектра. Значение S(0) при этом возрастает. При укорочении

(сжатии) импульса, наоборот, расстояние между нулями функции S( j ) увеличивается (расширение спектра), а значение S(0)

уменьшается. В пределе при 0 точки 2 , соответст-

вующие двум первым нулям функции S( j ) , удаляются в беско-

нечность, и спектральная плотность, бесконечно малая по величине, становится равномерной в полосе частот от до .

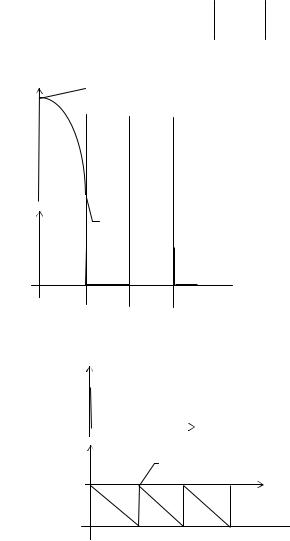
Модуль S( ) и аргумент ( ) спектральной плотности прямоугольного импульса приведены на рис. 2.8. Отметим, что

S( ) T2 A( ) , где A( ) – огибающая спектра периодической

последовательности прямоугольных импульсов.

56

При отсчете времени не от середины импульса, а от фронта (рис. 2.9,а), фазовая характеристика спектра импульса должна быть

дополнена слагаемым 2 , т.е.

S( j ) h sinc 2 e j ( ) 2 .

Результирующая фазовая характеристика изображена на рис. 2.9,б.

h

S( )

( ) 2 /

Рис. 2.8. Модуль и аргумент S( j ) одиночного прямоугольного импульса

x(t)		h
а)			t
( )			2 /
	2
б)

Рис. 2.9. Аргумент S( j ) сдвинутого прямоугольного импульса: а – сдвинутый прямоугольный импульс; б – аргумент

57

2.5.СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ПАЧКИ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ

Рассмотрим группу одинаковых и равноотстоящих импульсов

(рис. 2.10).	x(t)
		h

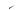
1 2 … N

T

(N 1)T

t

Рис. 2.10. Пачка прямоугольных импульсов

Спектральную плотность первого импульса в пачке обозначим S1 ( j ) . Тогда для второго импульса, сдвинутого относительно

первого на время T (в сторону запаздывания), спектральную функцию можно представить выражением

S2 ( j ) S1 ( j )e j T ,

для третьего импульса –

S3 ( j ) S1 ( j )e j 2 T ,

и так далее:

SN ( j ) S1 ( j )e j( N 1) T .

Таким образом, для группы из N импульсов в соответствии с принципом линейного суммирования спектров при сложении сигналов получим спектральную плотность

S( j ) S1 ( j ) 1 e j T e j 2 T ... e j ( N 1) T .

При частотах, отвечающих условию k 2T ( k – целое), каж-

дое из слагаемых в квадратных скобках равно единице и, следова-

тельно, S( jk	2 ) NS1 ( jk	2 ) . При частотах же	1	2 , а также
	T	T	N T

при некоторых других частотах, для которых сумма векторов

e j T обращается в нуль, суммарная спектральная плотность равна нулю.

58

x(t)

При промежуточных значениях частот модуль S( ) определя-

ется как геометрическая сумма спектральных плотностей отдельных импульсов (рис. 2.11).

S( )

N 3

3h

		2 /
1 2	2
3 T	T

Рис. 2.11. Пачка прямоугольных импульсов

2.6. ЭНЕРГЕТИЧЕСКОЕ ТОЛКОВАНИЕ СПЕКТРА СИГНАЛА

Пусть колебание представляет собой сложную периодиче-

скую функцию времени с периодом T . Энергия такого колебания, длящегося от до , бесконечно велика. Основной интерес представляют средняя мощность периодического колебания и распределение этой мощности между отдельными гармониками. Очевидно, что средняя мощность колебания, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период T .

Таким образом, средняя мощность

x2 (t) 1			Ck		2	k	2 Ck		2 C02 2 Ck		2 .
		t2 t1
			k				k		k 1

Используя тригонометрическую форму ряда Фурье и учитывая,

что C0			A	,			Ck							Ak
			0														, получаем
			2											2
								A			2									A			2		A	2		1				2
2								0												k					0
	x		(t)																											Ak		.	(2.6)
															2
								2									k 1		2						2			2 k 1
																					59

Если x(t) представляет собой ток i(t) , то при прохождении его

через сопротивление r			выделяется средняя мощность
						2		2
		2		2		I1		I2
r i			(t) r I0							...	,
						2		2
где I0 – постоянная составляющая, а Ik									– амплитуда k -й гармо-
ники тока i(t) .

Итак, средняя мощность равна сумме средних мощностей, выделяемых отдельно постоянной составляющей I0 и гармоника-

ми с амплитудами I1 , I2 ,... . Средняя мощность не зависит от фаз

отдельных гармоник.

Рассмотрим теперь распределение энергии в спектре неперио-

дического сигнала. Если функция	x(t) описывает непериодиче-
ский ток конечной длительности,	то Э x(t) 2 dt определяет

энергию, выделяемую током в резисторе в 1 Ом.

Для установления распределения энергии по спектру непериодического сигнала выразим Э через модуль спектральной плотности сигнала S( ) :

			2				1				j t
	Э		x(t) dt	x(t)				S( j )e				d dt
							2
	1				j t				1
		S( j ) x(t)e				dt d				S( j )S( j )d .
	2								2

Поскольку произведение комплексно-сопряженных величин можно представить как квадрат модуля спектральной плотности

S( j )S( j ) S( ) 2 , то энергию сигнала запишем в виде

		1		2	1		2
	Э			S( ) d			S( ) d .	(2.7)
		2
						0

Выражение (2.7), получившее название равенства Парсеваля, показывает, что энергия сигнала может быть представлена в виде

60