Березкин Основы теории информации и кодирования 2010

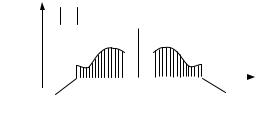
Ak

0 max	0	0	max

Рис. 1.9. Спектр сигнала, модулируемого по более сложному закону

Для неискаженной передачи такого сигнала канал связи должен обладать полосой пропускания частот равной 2 max , т.е. полоса

пропускания канала связи должна быть вдвое больше наивысшей частоты спектра модулирующего сигнала.

Иногда с помощью фильтров производится подавление несущей частоты и частот одной из боковых полос, т.е. передача производится в полосе частот max min .

1.5.ЧАСТОТНО-МОДУЛИРОВАННЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ

При частотной модуляции частота сигнала изменяется в общем виде по закону

(t) 0 [1 m f (t)] ,

где 0 – постоянная составляющая частоты; m – глубина

0

частотной модуляции; – наибольшее изменение частоты при модуляции (девиация частот); f (t) – закон модуляции. При из-

менении частоты всегда меняется фаза колебаний и наоборот. Этим определяется общий характер частотной (ЧМ) и фазовой (ФМ) модуляции. Иногда их объединяют под общим названием угловой модуляции. ЧМ осуществляется прямым воздействием датчика на генератор для изменения частоты его колебаний, хотя при этом меняется и фаза.

Здесь уместно напомнить некоторые соотношения для угловой

31

частоты колебаний, частоты в периодах и полной фазы колебания:

(t)	d п	;	f0		0		1	;	п (t) t	( )d 0 .
					2		T
	dt								0

Из этих соотношений видно, что частоту можно оценивать по скорости изменения фазы, а полную фазу – по интегральному значению угловой частоты.

Итак, частотно-модулированный сигнал можно представить в виде

x(t) A0 cos п (t) A0 cos[ (t) 0 ] A0 cos[ t ( )d 0 ]

		0
A0 cos[ 0t 0 m t		f ( )d 0 ] ,
	0
где (t) – текущая фаза сигнала;	0	– начальная фаза.

В частном случае, когда модуляция частоты осуществляется по

гармоническому				закону f (t) cos t, 0 ,		частотно-
модулированный сигнал может быть записан в виде
			x(t) A0 cos[ 0t 0 m t		cos d 0 ]
				0
			A0 cos[ 0t sin t 0 ] ,
где			– индекс модуляции. Сигнал такого вида представля-
ется следующим образом:
		x(t) A0		Jk ( ) cos[( 0 k )t 0 ] ,		(1.13)
				k
где	Jk ( ) – функция Бесселя первого рода k -го порядка от аргу-
мента .

Распределение амплитуд модулированного по частоте сигнала – дискретное, которое состоит из колебаний с несущей частотой 0 и бесконечного количества верхних и нижних боковых составляющих с частотами 0 k (рис. 1.10).

32

Ak

		0	0 k
k
0

Рис. 1.10. Спектр частотно-модулированного гармонического сигнала

При очень малом индексе модуляции ( 1) спектр частотно-

модулированного сигнала практически не отличается от спектра амплитудно-модулированного сигнала, так как он состоит всего из трех гармонических составляющих: колебаний с несущей частотой

0 и двух боковых с частотами 0 и 0 . В этом случае

полоса пропускания канала связи должна быть равна 2 .

С ростом увеличивается вес боковых составляющих и соот-

ветственно требуемая полоса пропускания. При больших индексах модуляции ( 1) ширина спектра сигнала практически равна

удвоенной величине девиации частоты ( 2 ) и не зависит от частоты модулирующего сигнала .

1.6. ФАЗОМОДУЛИРОВАННЫЙ ГАРМОНИЧЕСКИЙ СИГНАЛ

При этом виде модуляции фаза гармонического сигнала изменяется по закону модулирующего сигнала f (t)

(t) 0 [1 m f (t)] ,

где m – глубина фазовой модуляции; – наибольшее

0

изменение фазы при модуляции.

Сигнал с фазовой модуляцией можно представить в следующем виде:

33

x(t) A0 cos п (t) A0 cos[ 0t (t)]A0 cos[ 0t 0 m f (t) 0 ].

Так как мгновенное значение частоты является производной фазы по времени, то при фазовой модуляции оно может быть представлено в виде

(t) 0 0 m df (t) . dt

Таким образом, фазомодулированный сигнал эквивалентен сигналу с частотной модуляцией с модулирующей функцией dfdt(t) .

Для частного случая, когда модулирующий сигнал является гармоническим, полная фаза фазомодулированного сигнала определяется равенством

п(t) 0t 0m cos t 0 ,

а фазомодулированное колебание – выражением x(t) A0 cos[ 0t 0 m cos t 0 ].

Мгновенное значение частоты фазомодулированного колебания будет иметь вид

(t) d п 0 sin t 0 B sin t , dt

где B – девиация частоты фазомодулированного колеба-

ния.

Сравнение ЧМ и ФМ показывает, что при гармоническом модулирующем сигнале выражение, описывающее ЧМ колебание, отличается от такого же для ФМ колебания только фазой гармонической функции, определяющей изменение полной фазы высокочастотного колебания. В связи с этим по внешнему виду сигнала нельзя определить, как модулирован сигнал – по частоте или по фазе.

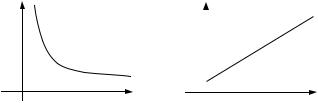
Однако при изменении частоты модуляции проявляется различие между ЧМ и ФМ (рис. 1.11).

В общем случае спектр колебания, модулированного по фазе одной частотой , выражается аналитически так же, как и спектр частотно-модулированного сигнала с такой же частотой (1.13).

34

	а)				б)			B
	Рис. 1.11. Зависимость девиации и индекса модуляции
	от модулирующей частоты:					B
	а – ЧМ (			); б – ФМ ( B ,			)

Помимо различия в структуре колебания, ЧМ и ФМ различаются по способу осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебаний генератора. При ФМ генератор дает стабильную частоту, а фаза колебания модулируется в одном из последующих элементов устройства.

1.7. ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ПРЯМОУГОЛЬНЫХ ИМПУЛЬСОВ

Графическое представление периодической последовательности прямоугольных импульсов приведено на рис. 1.12. Аналитическое выражение такой последовательности как функции времени имеет вид

h, -					iT t				iT ;
		2				2
x(t)
0,			iT t							(i 1)T,	i 0, 1, 2,... .
	2					2

С другой стороны, функция x(t) может быть представлена рядом Фурье

	x(t) A0					Ak cos(k 0t k )
			2
						k 1
		A0
			(ak cos k 0t bk sin k 0t) .
		2
				k 1
						35

Так как x(t) – четная функция, то b	0 и			bk
			arctg				0	.
k				a
		k
				k

Следовательно, x(t) A0 ak cos k 0t .

2 k 1

x(t)

h

…								…
				/2				t
		- /2
	-T/2				T/2

Рис. 1.12. Периодическая последовательность прямоугольных импульсов

Постоянная составляющая периодической последовательности

A

1

/ 2

h

прямоугольных импульсов принимает вид

0

hdt

, а

2

T

T

/ 2

амплитуда k - й гармонической составляющей

2

T / 2

2h

1

/ 2

ak

x(t) cos(k 0t)dt

T

d sin k 0t

T

k

T / 2

0

/ 2

2h

1

/ 2

h sin

k 0

(1.14)

sin k 0t

2

2

.

T

k

T

k 0

0

/ 2

2

Таким образом, разложение периодической последовательности прямоугольных импульсов в ряд Фурье представляется в следующем виде:

				sin		k 0
	h
						2
x(t)			2
		1
	T				k 0
			k 1
						2
				36

cos( k 0 t ) . (1.15)

Как видно из (1.14), при очередном приращении частоты на величину 2 фаза гармоник изменяется на величину .

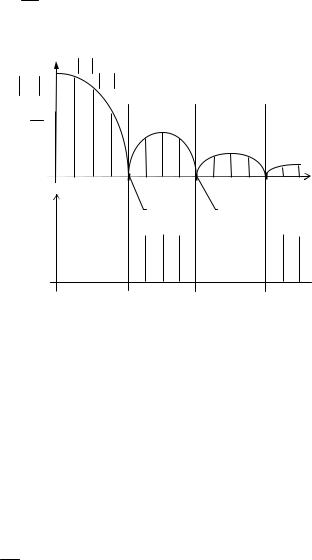
Спектры амплитуд и фаз последовательности прямоугольных импульсов представлены на рис. 1.13.

A1

Ak

A0

2

0 2 0 3 0	2	4
k

0 2 0 3 0

Рис. 1.13. Спектры амплитуд и фаз периодической последовательности прямоугольных импульсов

Причем огибающая спектра амплитуд определяется уравнением

	h			sin				k
A( ) 2							2				,
	T					k
							2

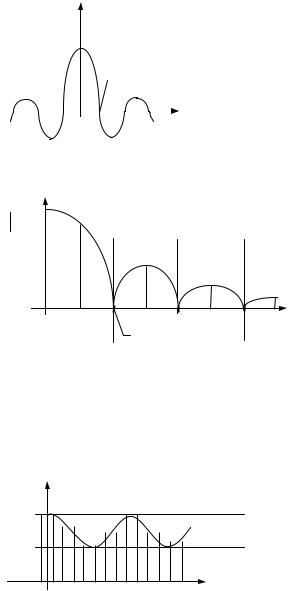
а форма огибающей – видом функции, приведенной на рис. 1.14. Номер k -й гармонической составляющей, попадающей в пер-

вый нуль функции sin с2 , определяется из соотношения

k 0 2 , откуда получаем k T [15]. Например, при T 2

спектр амплитуд имеет вид, приведенный на рис. 1.15.

37

			sin
sinc	2		2
					1
			2
						2

		sin
	lim		2	1 ,
	0
		2
	sin		0, при n
		2			, n четное.
	2

				Рис. 1.14. Функция sinс
									2
Ak
	A0						A3
2

	0		2
		2 0

Рис. 1.15. Спектр амплитуд последовательности T 2

1.8. АМПЛИТУДНО-МОДУЛИРОВАННАЯ ПЕРИОДИЧЕСКАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ ИМПУЛЬСОВ

Пусть амплитуда прямоугольных импульсов модулируется по гармоническому закону (рис. 1.16) h(t) h0 [1 mh cos t].

x(t)

h0

h0 (1 mh )

h0

(1 mh )

t

Рис. 1.16. Амплитудно-модулированная последовательность импульсов

38

Подставив h(t) в выражение (1.15) для немодулированной по-

следовательности прямоугольных импульсов, получим выражение для амплитудно-модулированной последовательности

							sin		k 0
	h0	1 m		cos t 1
									2
x(t)			h		2
	T							k 0
						k 1
									2

cos( k 0t) .

После тригонометрических преобразований будем иметь

sin

k

0

h

h

2

0

2

0

cos t

x(t)

1

cos( k 0 t)

mh

T

k 0

T

k 1

2

h0

sin

k 0

2

cos (k 0

)t

mh

T

k 0

k 1

2

h0

sin

k 0

2

cos (k 0

)t .

mh

T

k 0

k 1

2

Сравнивая полученное выражение с разложением для периодической последовательности немодулированных импульсов, видим, что в результате амплитудной модуляции импульсов в спектре, кроме постоянной составляющей и составляющих с частотами,

кратными основной частоте 0 , появились составляющая с часто-

той модуляции , а также по две боковые составляющие (нижняя k 0 и верхняя k 0 ) около каждой k - й гармоники основной частоты (рис. 1.17).

Появление боковых частот k 0 практически не сказывается на ширине спектра сигнала, так как частота модуляции0 . В связи с этим практическая ширина спектра амплитуд-

но-модулированной последовательности импульсов такая же, как и соответствующей последовательности немодулированных импуль-

39

сов, т.е. определяется длительностью импульсов.

Ak		0
		0

h0

T

	0	2 0	3 0	2

Рис. 1.17. Спектр амплитуд модулированной последовательности

ЗАДАЧИ

1.1. Доказать тождественность комплексной и тригонометрической форм обобщенного ряда Фурье

x (t ) 1
			Ak e jk 0 t ,
x(t ) A0		2 k
		Ak cos( k 0 t k ) .
2		k 1

1.2. Найти спектр периодической последовательности прямоугольных импульсов (рис. 1.18)

			T	iT ;
h, iT t
			2
x(t)	T
		iT	t iT,				i 0, 1, 2,...,
h,
	2
называемой меандром.				x(t)
						h			t
-T/2				T/2
Рис. 1.18. Меандр
		40