Логинов Избранные разделы курса Векторный анализ (теория и примеры) 2009

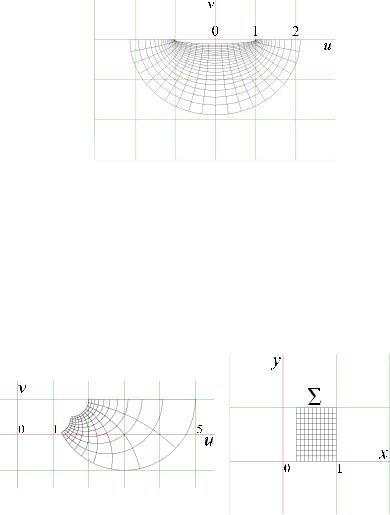
Образ области Σ при отображении функцией Жуковского показан на рис. 1.9.

Рис. 1.9

Дробно-линейное отображение. Здесь приводится некоторый частный случай дробно-линейного отображения. На рис. 1.10 показан вид образа области Σ= [0.25,1]×[0,1] при отображении

u = 1	+				x
				2 + y		2
			x
					y		, ( x, y) Σ .
v = 1	−
			x	2	+ y	2

Рис. 1.10

11

1.2.4. Замена переменных в двойном интеграле

ξ = ξ( x, y)

Рассмотрим отображение , ( x, y) D и его обратное

η = η( x, y)

x = x(ξ, η)

отображение , (ξ, η) Σ . Будем предполагать, что это y = y(ξ, η)

отображение непрерывно дифференцируемо в области D и имеет там отличный от нуля якобиан.

Теорема. Пусть функция f интегрируема в D, тогда

	∫∫ f (x, y)dxdy = ∫∫ f [ x(ξ, η), y(ξ, η)]		D( x, y)		dξdη .
			D(ξ, η)
	D	Σ

Пример 1.2. Рассмотреть область D={ϕ [α,β],r [r1,r2]} (рис. 1.11) и сделать замену в интеграле ∫∫ f ( x, y)dxdy , используя по-

D

лярные координаты

x = r cos ϕ

, ϕ [ϕ1, ϕ2 ], r [r1, r2 ] . y = r sin ϕ

Рис. 1.11

12

Решение. Для полярных координат вычисляем якобиан отобра-

жения	D( x, y)	=	− r sin ϕ	cos ϕ	= −r ,		D( x, y)		= r . Поэтому для
	D(ϕ, r)		r cos ϕ	sin ϕ			D(ϕ, r)
областей указанного типа получим
				ϕ2		r2
	∫∫ f ( x, y)dxdy = ∫ dϕ ∫ f (r cos ϕ,r sin ϕ)rdr =
	D			ϕ		r
				1		1
			r2	ϕ2
			= ∫rdr ∫ f (r cos ϕ,r sin ϕ)dϕ .
			r	ϕ
			1	1

Пример 1.3. Сделать замену переменных u=x+y, v=y – x в интеграле ∫∫ f ( x, y)dxdy для области D={|x|+|y|≤ 1} (рис. 1.12 слева).

D

Рис. 1.12

Решение. В координатах u, v область Σ является квадратом со сторонами параллельными координатным осям (рис. 1.12 справа).

Якобиан отображения						D(u, v)		=	1	1	= 2 . Нужный нам якоби-
						D(x, y)			−1	1
	D( x, y)		1
ан равен		=			. Поэтому
	D(u, v)	2

13

					u − v						u + v			1
∫∫ f ( x, y)dxdy = ∫∫ f										,					dudv =
														2
D				Σ	2							2
	1	1	1	u − v u + v
=		∫du ∫		f			,					dv .
	2	−1	−1		2				2

Пример 1.4. Сделать замену переменных x=u cos4v, y= u sin4v в интеграле ∫∫ f (x, y)dxdy для области D, ограниченной осями коор-

D

динат x=0, y=0 и аркой астроиды x + y = a (рис. 1.13).

D

Рис. 1.13

Решение. Отображение x=u cos4v, y= u sin4v является обобщенными полярными координатами, где параметр v имеет смысл угла, а параметр u является радиусом обобщенных полярных координат. Поэтому область интегрирования D в обобщенных координатах (u, v) описывается, как прямоугольник Σ = [0,1]×[0, π / 2] . Якоби-

ан отображения будет равен

D( x, y)	=	cos 4 v	− 4u cos3 v sin v	= 4u sin 3 v cos5 v +
D(u, v)		sin 4 v	4u sin 3 v cos v

+ 4u cos 3 v sin 5 v = 4u sin3 v cos3 v .

Тогда

14

π

12

∫∫f (x, y)dxdy = 4∫udu ∫ f (u cos 4 v, u sin 4 v)sin 3 v cos3 vdv .

D

0

0

Пример 1.5. Является ли конечной площадь области, заключенной между биссектрисой второго–четвертого координатных углов и кривой (x3+y3)2=x2+y2 (рис. 1.14).

Рис. 1.14

Решение. В полярных координатах уравнение заданной области

имеет вид r6(cos3ϕ+sin3ϕ)2=r2, r =		1		. Тогда площадь
		cos3 ϕ + sin3 ϕ
указанной области будет равна

									3					1
											π
														cos 3 ϕ+sin 3 ϕ
								4
					µD= ∫∫dxdy = ∫ dϕ									∫rdr
							D	−			π			0
								4
			3		π
	1	4						dϕ
=			∫												=
2		−			π		(cos ϕ + sin ϕ)(1 − cos ϕ sin ϕ)
					4

						3				π
		1			4									dϕ
=								∫										=
2					−					π cos3 ϕ + sin 3							ϕ
										4
					3			π
1					4											dϕ
						∫									π				=
2
			− π sin(ϕ +													)(2 − sin 2ϕ)
							4							4

15

															3			π
												1		4																	dϕ
									=																																			=
																∫												π									π
												2
															−			π sin(ϕ +												)(2 + cos(2(ϕ +									)))
																											4										4
																		4
																3			π											d cos(ϕ +				π
												1		4																					)
									= −																									4												=
																∫														π									π
												2													2	(ϕ +					)(2 + cos(2(ϕ +
															−				π sin																						)))
																														4									4
																		4
					3		π								d cos(ϕ +												π
	1		4																										)										1				−1					du
																											4
= −					∫																															= −								∫					.
																				π												π
	2						π		(1 − cos2			(ϕ +												))(1 + 2 cos2 (ϕ +									))						2			1				(1	− u	2 )(1 + 2u 2 )
				−
							4											4													4

Этот интеграл расходится и область не имеет конечной площади.

1.3.Тройные интегралы

1.3.1.Сведение тройного интеграла к повторному для прямоугольного параллелепипеда

Пусть V – прямоугольный параллелепипед [a,b]× [c,d] × [g,h] и функция f(x,y,z) определена на V. Проекцию этой области на плоскость x=0 обозначим D через (рис. 1.15). Эта область представляет собой прямоугольник [c,d] × [g,h].

Рис. 1.15

16

Теорема. Если существует ∫∫∫ f ( x, y, z)dxdydz и для любого

V

x [a,b] существует ∫∫ f ( x, y, z)dydz , то существует инте-

D

b

грал ∫dx∫∫ f ( x, y, z)dydz и имеет место равенство

aD

b

∫dx∫∫ f ( x, y, z)dydz = ∫∫∫ f ( x, y, z)dxdydz .

a D

V

В формулировке теоремы и в дальнейшем используются обозначения

b		b
∫dx∫∫ f ( x, y, z)dydz = ∫			∫∫ f ( x, y, z)dydz dx .
a	D	a	D

В свою очередь, внутренние двойные интегралы можно представить в виде повторных интегралов. Для первого из написанных соотношений это будет выглядеть следующим образом:

b	d	h
∫dx∫dy ∫ f ( x, y, z)dz = ∫∫∫ f ( x, y, z)dxdydz ,
a	c	g	V
b	h	d
∫dx∫dz∫ f (x, y, z)dy = = ∫∫∫ f ( x, y, z)dxdydz ,
a	g	c	V

где используются обозначения:
b	d	h	b d h
∫dx∫dy ∫ f ( x, y, z)dz = ∫				∫ ∫ f ( x, y, z)dz dy dx .
a	c	g	a c g

Можно собирать внешние повторные интегралы в двойные, в результате получатся равенства:

17

h

∫∫dxdy∫ f ( x, y, z)dz = ∫∫∫ f ( x, y, z)dxdydz,

Dxy	g	V
	d

∫∫dzdx∫ f ( x, y, z)dy = = ∫∫∫ f ( x, y, z)dxdydz .

Dzx c V

Для другой координатной плоскости получим

b

∫∫dydz∫ f ( x, y, z)dx = ∫∫∫ f ( x, y, z)dxdydz ,

Dyz

a

V

здесь Dxy =Dz =[a,b] [c,d], Dzx=Dy =[g,h] [a,b] , Dyz =Dx =

=[c,d] [g,h].

1.3.2.Сведение тройного интеграла к повторному интегралу для областей общего вида

Пусть V – область, расположенная между плоскостями x=a, x=b. Через Lx обозначим плоскость, параллельную координатной плоскости Oyz и проходящую через точку x. Для точек x [a,b] обозначим через Dx сечение области V плоскостью Lx . Будем предполагать, что Dx квадрируема для всех x [a,b]. При этих предположениях справедлива следующая теорема:

Теорема. Если существует ∫∫∫ f ( x, y, z)dxdydz и для любого

V

x [a,b] существует интеграл I(x)= ∫∫ f ( x, y, z)dydz , то существу-

Dx

b

ет и повторный интеграл ∫dx ∫∫ f ( x, y, z)dydz , и этот интеграл

aDx

будет равен тройному интегралу

b

∫dx ∫∫ f ( x, y, z)dydz = ∫∫∫ f ( x, y, z)dxdydz.

a Dx V

18

Указанные в формулировке теоремы области показаны на рис. 1.16.

Рис. 1.16

Замечание. Сечение Dx=V∩ Lx может быть задано в виде

Dx = {(y,z): y1(x)≤y≤ y2(x) , z1(x,y)≤z≤z2(x,y)}.

В этом случае пределы интегрирования в тройном интеграле можно расставить следующим образом:

by2 ( x) z2 ( x, y)

∫∫∫ f ( x, y, z)dxdydz	= ∫dx	∫ dy	∫ f ( x, y, z)dz =
V	a	y1 ( x)	z1 ( x, y)
	z2 ( x, y)
= ∫∫dxdy	∫ f ( x, y, z)dz ,

Dz1 ( x, y )

где D – представляет собой проекцию области V на плоскость z=0. Эта проекция описывается неравенствами D = {(x,y):a ≤ x ≤ b, y1(x)≤ y ≤ y2(x)}. Расставляя переменные x, y, z в другом порядке, можно получить другие аналогичные формулы представления тройного интеграла через повторные интегралы.

19

1.3.3.Замена переменных в тройном интеграле

Пусть задано взаимно-однозначное, непрерывно-дифференци- руемое отображение

x = x(ξ, η, ζ)

y = y(ξ, η, ζ) , (ξ, η, ζ) Σ

z= z(ξ, η, ζ)

сякобианом, отличным от нуля, переводящее область Σ в область V, где области Σ и V кубируемы.

Вэтом случае для объема области V справедлива формула

	µ V = ∫∫∫		D( x, y, z)		dξ dη dζ .
			D(ξ, η, ζ
	Σ

Теорема (о замене переменных). Если f интегрируема в V, то

∫∫∫ f ( x, y, z) dx dy dz =

V

	= ∫∫∫ f [ x(ξ, η, ζ), y(ξ, η, ζ), z(ξ, η, ζ)]		D( x, y, z)		dξ dη dζ .
			D(ξ, η, ζ
	Σ

Пример 1.6. Цилиндрические координаты. Вычислить интеграл

∫∫∫ x2 + y2 dx dy dz ,	где			область			интегрирования
V
V = {x2 + y 2 = z 2 ,0 ≤ z ≤ 1} представляет собой конус (рис. 1.17).
Решение. Воспользуемся цилиндрическими координатами
	x = r cos ϕ
				D( x, y, z)		= r .
	y = r sin ϕ ,
				D(r, ϕ, h)
	z = h		20