Логинов Избранные разделы курса Векторный анализ (теория и примеры) 2009

	i		j		k
rot V = =	∂		∂		∂			=(-1,-1,-1).
	∂x		∂y		∂z
	y		z		x

В качестве поверхности с краем C выберем круг, полученный в сечении плоскостью x+y+z=0 шара x2+y2+z2≤ a2 и ориентированный нормалью (1,1,1) (рис. 3.11).

Рис. 3.11

Тогда
∫ ydx + zdy + xdz = ∫∫		(rot V, dS)= ∫∫ (rot V, n)
C	Φ	Φ

dS = −3 ∫∫dS = = −3 µФ= − 3 π a2.

Φ

Пример 3.7. Вычислить интеграл

∫( x2 − yz)dx + ( y2 − xz)dy + (z2 − xy)dz ,

AmB

взятый по отрезку винтовой линии x=a cos ϕ , y=a sin ϕ , z= h ϕ

2π

от А(а,0,0) до B(a,0,h) (рис. 3.12).

Рис. 3.12

61

		i		j		k
Решение. rot V =		∂		∂		∂			=
		∂x		∂y		∂z
	x2 − yz y 2 − xz z 2 − xy

= (−x + x, − y + y, −z + z) =(0,0,0), поэтому интеграл не зависит от пути интегрирования и вместо винтовой линии выберем отрезок,

x = a

соединяющий точки A, B. y = 0 , t [0, h] . Тогда интеграл будет z = t

равен

h

h

3

∫( x2 − yz)dx + ( y2 − xz)dy + (z2 − xy)dz = ∫t 2dt =

.

3

AmB

0

Пример 3.8. Доказать формулу

1

dx

dy

dz

1

∫([n, r], ds), где Ф – область, ле-

µΦ =

∫

cos α

cos β

cos γ

= =

2

∂Φ

x

y

z

2

∂Φ

жащая в плоскости с единичной нормалью n , ограниченная кривой ∂Φ , c согласованной ориентацией.

Решение. Находим векторное поле

V = [n, r] = ( z cos β − y cos γ, x cos γ − z cos α, y cos α − x cos β) ,

далее вычисляем ротор этого поля

		i			j			k
rot V =		∂			∂			∂			=
		∂x			∂y			∂z
	z cosβ − y cos γ			x cos γ − z cos α			y cos α − x cosβ

62

= (2 cos α,2 cos β,2 cos γ) =2 n .

По формуле Стокса получим

	dx	dy	dz	= ∫(V , ds)= ∫∫(rot V ,dS )= ∫∫(2n, n)dS =
∫	cos α	cos β	cos γ
∂Φ	x	y	z	∂Φ	Φ	Φ

= 2∫∫dS = 2µΦ ,

Φ

откуда и следует требуемое соотношение.

Пример 3.9. Вычислить ∫( y − z)dx + (z − x)dy + ( x − y)dz , где С –

C

контур x=a sin2t, y=a sin t cos t, z=a cos2t , t [0,π].

Решение. Контур лежит в плоскости x+z=a (рис. 3.13) , далее

x

y

a

2

a

2

= tg t =

, y2=x z , y2=x (a – x) , или

x −

+ y 2

=

. Таким

y

z

2

4

образом, этот контур является эллипсом с полуосями

a

,

a

(рис.

2

2

3.14).

Рис. 3.13

63

	Рис. 3.14
		i			j			k
Вычисляем ротор rot V =		∂			∂			∂		= (−2,−2,−2) , для
		∂x			∂y			∂z
	y − z			z − x			x − y

вектора нормали n = 1 (1,0,1) определяется скалярное произведе-

2

ние (rot V , n)= −2

2 . Тогда интеграл будет равен

∫( y − z)dx + ( z − x)dy + ( x − y)dz = ∫∫(rot V ,dS )= − 2

∫∫dS =

2

C

Φ

Φ

= −2

π

a

a

= −πa2 .

2

2

2

3.3.3. Условия независимости криволинейного интеграла от пути интегрирования в пространстве

Определение. Область D называется поверхностно односвяз- ной, если для любой кусочно гладкой замкнутой кривой Г (контура Г), лежащей в D, можно указать ориентированную допустимую

поверхность Ф, расположенную в D, краем которой является Г.

Например, шар является поверхностно односвязной областью, тор не является поверхностно односвязной областью (рис. 3.15).

64

Рис. 3.15

Теорема 1. Для того, чтобы интеграл ∫ Pdx + Qdy + Rdz не за-

висел от пути в поверхностно односвязной области D, необходимо и достаточно, чтобы rot V =0 в области D.

Теорема 2. Для того, чтобы интеграл ∫ Pdx + Qdy + Rdz не за-

висел от пути интегрирования в поверхностно односвязной облас- ти D , необходимо и достаточно, чтобы подынтегральное выра- жение было полным дифференциалом

Pdx+Qdy+Rdz = du.

3.4. Формула Остроградского–Гаусса

Определение. Объемно односвязной областью называется об- ласть D, удовлетворяющая следующему свойству. Любая замкну- тая кусочно-гладкая не самопересекающаяся поверхность, распо- ложенная в D , является границей области целиком лежащей в D. Можно сказать, что объемно односвязная область характеризу-

ется отсутствием полостей внутри области.

Если в объемно односвязной области W задано поле V=(P,Q,R) c непрерывными частными производными по соответствующим переменным, то справедлива формула

∂

∂

∂

+

+

P +

Q +

R

∫∫∫

dxdydz =

∫∫Pdydz

Qdzdx

Rdxdy .

∂x

∂y

∂z

W

∂W

65

Дивергенция векторного поля определяется по формуле

div V = ∂P + ∂Q + ∂R . ∂x ∂y ∂z

Тогда, используя векторные обозначения, формулу Остроград- ского–Гаусса можно записать в виде

∫∫∫	div V dW = ∫∫ (V,dS).
W	∂W

Формула Остроградского–Гаусса будет верна и для областей, допускающих разбиение на конечное число областей указанного типа.

Пример 3.10. Вычислить интеграл

I = ∫∫(x − y + z)dydz + ( y − z + x)dzdx + (z − x + y)dxdy ,

Φ

Φ = {| x − y + z | + | y − z + x | + | z − x + y |= 1} .

Решение. Поверхность Φ показана на рис. 3.16.

Рис. 3.16

66

По формуле Остроградского–Гаусса I =3 ∫∫∫dxdydz . Сделаем

	B
u = x − y + z
замену переменных v = y − z + x , в этом случае в новых коорди-
w = z − x + y
натах граница области ∂	будет определяться уравнением

|u|+|v|+|w|=1. Якобиан отображения равен

1−1 1

D(u, v, w)

= 1

1

−1 = 2 + 2 = 4. Для

обратного отображения

D( x, y, z)

1

1

−1

якобиан будет равен

D(x, y, z)

=

1

, поэтому интеграл I будет ра-

D(u, v, w) 4

3

вен

3

∫∫∫dudvdw =

2

2 2

=1.

4

4

3

Пример 3.11.

Доказать, что если Ф – замкнутая простая поло-

жительно ориентированная поверхность,

то ∫∫(a, dS )=0, где a –

Φ

постоянное векторное поле.

Решение. Утверждение непосредственно следует из формулы Остроградского–Гаусса.

Пример 3.12. Объем области W равен µW = 1 ∫∫(r, dS ), где ∂W –

3 ∂W

положительно

следует из формулы Остроградского–Гаусса. ориентированная граница области W.

Решение. Утверждение непосредственно

Пример 3.13. Объем конуса, ограниченного гладкой конической поверхностью F(x,y,z)=0 и плоскостью с единичной нормалью m

67

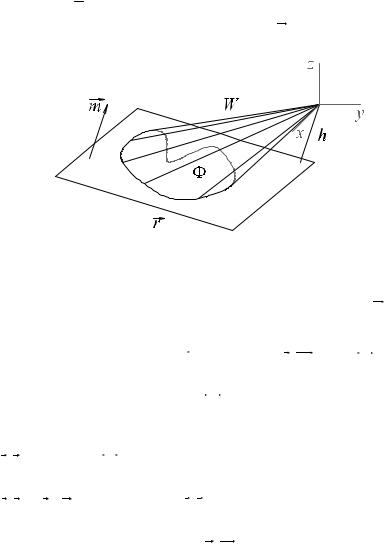
равен µW = 1 hµΦ , где µΦ – площадь основания, h – высота кону- 3

са (рис. 3.17). Предполагается, что нормаль m к плоскости направлена в сторону вершины конуса.

Рис. 3.17

Решение. Поместим начало координат в вершину конуса. Боковую поверхность конуса, ориентированную внешней нормалью,

обозначим Ф1 , а основание, ориентированное нормалью − m , обозначим Ф2 . Тогда

3µW = ∫∫∫3dxdydz =∫∫∫div r dxdydz =		∫∫(r, dS )= ∫∫(r, n)dS )+
W	W	∂W	Φ1
	+ ∫∫(r, n)dS .
	Φ2

Для	боковой поверхности	конуса скалярное произведение
(r, n)= 0	и ∫∫(r, n)dS = 0 . Для	поверхности основания конуса
	Φ1
(r, n)= (r,−m)= h , поэтому ∫∫(r, n)dS = h ∫∫dS = hµΦ .
	Φ2	Φ2

Пример 3.14. Вычислить ∫∫(V , dS ), где Ф – часть конической

Φ

68

поверхности x2+y2=z2 , 0≤ z ≤ a, ориентированной внешней нормалью, а поле V = (x2 , y2 , z 2 ) .

Решение. Дополним поверхность до замкнутой поверхности. Основание, ориентированное нужным образом, обозначим Ф0, тогда интеграл по замкнутой поверхности будет вычисляться по формуле Остроградского–Гаусса

∫∫(V , dS )= ∫∫∫div V dxdydz = 2∫∫∫(x + y + z) dxdydz =

Φ+Φ0		W			W
2π	a	h						2π		a	h
= 2 ∫dϕ∫dh∫r(r cos ϕ + r sin ϕ + h)dr = 2 ∫ dϕ∫dh∫rhdr =
0	0	0						0		0	0
		a	h		a			π
		= 4π∫hdh∫rdr = 2π∫h3dh =							a4 .
								2
		0	0		0
Интеграл по верхней части поверхности будет равен
		∫∫(V , dS )= ∫∫a2dxdy = a2µD = πa2 .
		Φ0	D
Таким образом,		∫∫(V , dS )=	π	a4 − πa4 = −		π	a4 .
			2
		Φ			2

3.5.Элементы теории поля

3.5.1.Основные определения

Для вектора будет использоваться обозначение a или a . Функция u(x,y,z) , заданная в области D, будет называться скалярным полем. В случае задания трех функций P, Q, R можно говорить о векторном поле V=(P,Q,R).

Градиент скалярного поля u определяется как векторное поле

		∂u		∂u		∂u
	V = grad u =		,		,		.
	∂x			∂y		∂z

69

Функция u называется потенциалом векторного поля, а само поле называется потенциальным. Связь между потенциалом и координатами векторного поля задается соотношением

du=Pdx+Qdy+Rdz .

Определение 1. Интеграл ∫ (V, ds) для замкнутой кривой С на-

C

зывается циркуляцией векторного поля по C. Замкнутая кривая называется контуром, а интеграл по контуру обозначается

∫ (V, ds) и представляет собой работу векторного поля вдоль

C

этого контура. Поле называется безвихревым, если его ротор ра- вен нулю.

Определение 2. Поле V называется соленоидальным, если для него существует векторное поле W, такое, что V = rot W. Такое

векторное поле W называется векторным потенциалом поля V .

Упомянутые ранее утверждения можно сформулировать в виде теоремы.

Теорема (условия потенциальности поля). Пусть в поверхност- но односвязной области D задано непрерывно дифференцируемое поле V=(P,Q,R). Тогда эквивалентны следующие три условия:

1)	циркуляция векторного поля ∫ (V, ds) равна нулю
	C

вдоль любого контура, лежащего в D;

2)поле V потенциальное, т. е. существует дважды непрерывно дифференцируемая функция, градиентом которой и являет-

ся данное поле. При этом ∫ (V, ds) = u(B) - u(A);

AB

3)поле V безвихревое.

3.5.2.Поток векторного поля

Будем считать, что V=(P,Q,R) – это поле скоростей (рассматривается стационарный поток жидкости). Векторной линией поля V

70