Семестровая по математике

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

Кафедра высшей математики

Векторная алгебра и аналитическая геометрия

Индивидуальные задания

Новокузнецк

2014

УДК 514.7(07)

В 269

Рецензент

доктор физико-математических наук, доцент

кафедры физики имени профессора В.М. Финкеля

Коваленко В.В.

В 269 Векторная алгебра и аналитическая геометрия. Индивидуальные задания: метод. указ. / Сиб. гос. индустр. ун-т; сост. В.В. Варламов. – Новокузнецк : Изд. центр СибГИУ, 2014. – 28 с.

В работе приведены краткие теоретические сведения по теме «Векторная алгебра и аналитическая геометрия», разобраны примеры решения задач и даны задания для самостоятельной работы по этой теме.

Предназначены для практических занятий по теме «Векторная алгебра и аналитическая геометрия» для всех направлений подготовки, включающих изучение дисциплины «Математика».

Печатается по решению Совета Института фундаментального образования

2

Теоретические сведения

Определение. Векторы a1 ,...,an называются линейно зависимы-

ми, если существует такая линейная комбинация

1 a1 2 a2 ... n an 0 , при не равных нулю одновременно i , т.е.

12 22 ... n2 0.

Если же только при i = 0 выполняется 1 a1 2 a2 ... n an 0 ,

то векторы называются линейно независимыми.

Пример. Даны векторыa =(1; 2; 3), b =(-1; 0; 3), с =(2; 1; -1) и d =(3; 2; 2) в некотором базисе. Показать, что векторы a , b и с образуют

базис и найти координаты вектора d в этом базисе.

Векторы образуют базис, если они линейно независимы, другими словами, если уравнения, входящие в систему:

2 0
	линейно независимы.
2 0 0
3 3 0

Тогда d a b c .

Это условие выполняется, если определитель матрицы системы отличен от нуля.

1 1 2

20 1 0

33 1

3

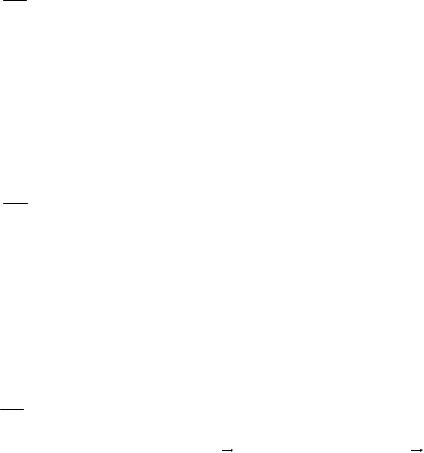
1	1		2		0			1					2	1		2		2	0		3 ( 2 3) 12 4 0
2	0		1		1	1							3	1				3	3
3	3		1
a1 b1 c1 d1
			b2		c2 d2									Для решения этой системы воспользуемся
a2
			b		c			d
a		3					3				3
			3

методом Крамера.

		d1	b1	c1		3	1	2			0	1		2	1		2	0
		d2	b2	c2		2	0	1		3						2
1	=										3	1		2	1		2	3
		d3	b3	c3		2	3	1

3( 3) ( 2 2) 12 1.

1 1/ 4;

		a1	d1	c1		1	3	2
2	=	a2	d2	c2		2	2	1	( 2 2) 3( 2 3) 2(4 6)
		a3	d3	c3		3	2	1

4 15 4 7;

2 7 / 4;

		a1	b1	d1		1	1	3
3	=	a2	b2	d2		2	0	2	6 (4 6) 18 10;
		a3	b3	d3		3	3	2

3 5/ 2;

Итого, координаты вектора d в базисе a , b , с : d =( -1/4, 7/4, 5/2).

4

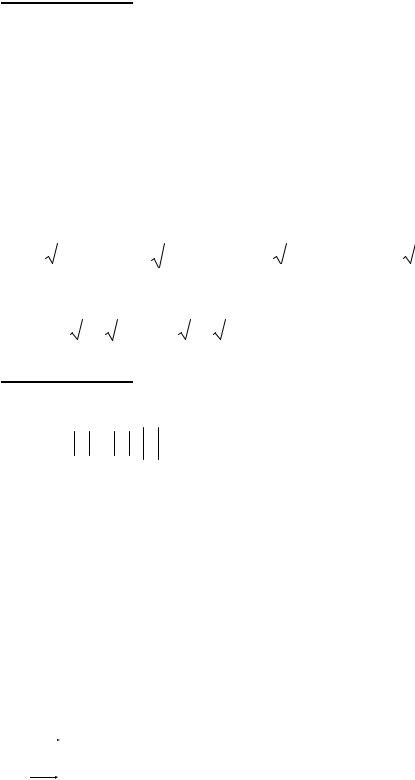
Определение. Скалярным произведением векторов a и b назы-

вается число, равное произведению длин этих сторон на косинус угла между ними

																															2 j 3k ,
Пример. Найти угол между векторами a и b , если a i
b 6i 4 j 2k .
Т.е. a = (1, 2, 3),													b = (6, 4, -2)
a b = 6 + 8 – 6 = 8:
																	b
			1 4 9								14;											36 16 4				56 .
	a
cos =				8									8								4			2	;	arccos			2	.
																				14
				14			56				2		14		14								7			7

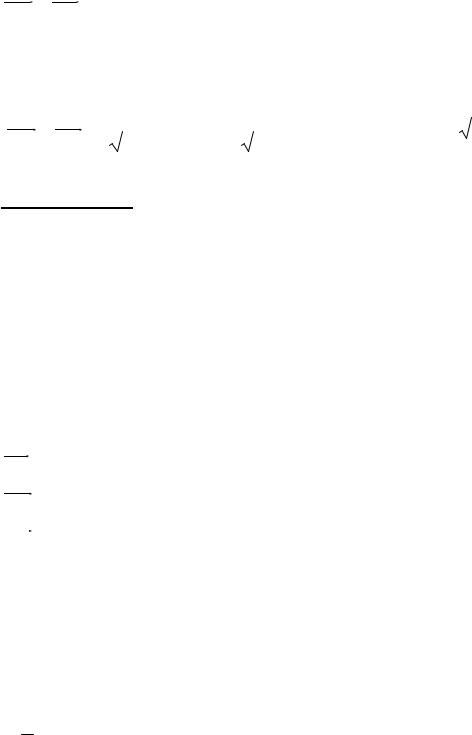
Определение. Векторным произведением векторов a и b называ-

ется вектор c , удовлетворяющий следующим условиям:

1)c a b sin , где - угол между векторами a и b ,

sin 0;

0

2)вектор c ортогонален векторам a и b

3)a , b и c образуют правую тройку векторов.

Обозначается: c	a b	илиc	[a,b].

Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2),

В(4, 0, 3),

С(0, 1, 0).

AC (0 2;1 2;0 2) ( 2; 1; 2)

AB (4 2;0 2;3 2) (2; 2;1)

5

	AC AB				i		j	k					1		2				2	2						2			1
					2		1	2
										i			2		1		j		2	1		k				2			2
					2		2	1
i ( 1 4) j( 2 4) k (4 2) 5i 2 j 6k.
																												(ед2).
	AC AB																			S				65
						25 4 36					65.
																							2

Определение. Смешанным произведением векторов a , b и c на-

зывается число, равное скалярному произведению вектора a на век-

тор, равный векторному произведению векторов b и c .

Обозначается a b c или (a , b ,c ).

Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).

Найдем координаты векторов:

BA ( 2; 3; 4)

BD (1;4; 3)

BC (4; 1; 2)

Объем пирамиды

		1		2	3	4		1
	V			1	4	3			( 2( 8 3) 3( 2 12) 4( 1 16))
	6			4	1	2	6

1 (22 30 68) 20(ед3 ) 6

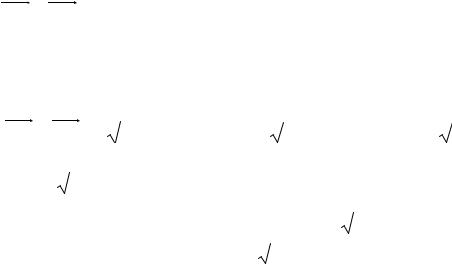
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.

6

						i				j			k
	BD BC					1		4					3
														i ( 8 3) j( 2 12) k ( 1 16)
						4			1				2
11i 10 j 17k.
	BD BC
								112				102		172						121 100 289									510
Sосн =							/ 2(ед2)
		510
			Sосн h											3V					120				4				.(ед)
Т.к. V =									;				h												510
																								17
		3												Sосн					510

		Задачи для самостоятельного решения
Задача 1. Написать разложение вектора x по векторам p,																q, r.
1.1. x 2,		4,		7 , p 0,		1,	2 ,q 1,			0,	1 ,		r 1,			2,	4 .
1.2.x 6,	12,		1 , p 1,			3,	0 ,		q 2,	1,		1 , r 0,				1,	2 .
1.3.x 1,	4,		4 , p 2,			1,	1 ,		q 0,	3,		2 ,		r 1,		1,	1 .
1.4. x 9,		5,		5 ,	p 4,	1,	1 , q 2,			0,		3 ,		r 1,		2,	1 .
1.5.x 5,		5,		5 , p 2,			0,	1 ,q 1,		3,		1 ,r 0,				4,	1 .
1.6. x 13,		2,		7 ,	p 5,	1,	0	, q 2,		1,		3 , r 1,				0,	1 .
1.7.x 19,		1,		7 , p 0,			1,	1 , q 2,			0,		1 , r 3, 1,				0 .
1.8. x 3,		3,		4 ,	p 1,	0,	2 ,		q 0,	1,		1 ,	r 2,		1,		4 .
1.9. x 3,		3,	1 ,		p 3,	1,	0 , q 1,			2,		1 ,		r 1,		0,	2 .

7

1.10.x 1,	7,	4 , p 1,						2,	1 ,q 2,			0,		3 ,r 1,			1, 1 .
1.11.x 6,	5,	14 , p 1,					1,	4 ,q 0,				3,		2 ,r 2,			1, 1 .
1.12.x 6,	1,	7 , p 1,					2,		0 , q 1,				1,	3 , r 1,			0,		4 .
1.13.x 5,	15,	0 ,		p 1,		0,		5 , q 1,				3,		2 ,	r 0,		1,		1 .
1.14.x 2,	1,	11		, p 1,			1,	0 ,		q 0,	1,			2 , r 1,			0,		3 .
1.15.x 11,	5,	3		, p 1,			0,	2 ,q 1,				0,		1 ,r 2,			5,		3 .
1.16. x 8,	0,	5 ,		p 2,		0,		1 , q 1,			1,		0 , r 4,			1,	2 .
1.17.x 3,	1,	8 ,	p 0,		1,		3 ,		q 1,		2,		1 , r 2,			0,		1 .
1.18.x 8,	1,	12	,	p 1,		2,		1 ,		q 3,		0,		2 ,	r 1,		1,		1 .
x 9,	8,		3 , p 1,					4, 1 , q 3,					2, 0 ,
1.19.	1,	2 .
r 1,
x 5,	9, 13 , p 0, 1,								2 , q 3,				1,		1 ,
1.20.	1,	0 .
r 4,
1.21.x 15, 5,			6 ,p 0,				5,	1 ,q 3,			2,		1 ,r 1,				1,		0 .
1.22. x 8,	9,	4 ,		p 1,		0,		1 , q 0,			2,			1 ,	r 1,	3,		0 .
x 23,	14,		30 ,		p 2,				1,	0 , q 1,				1,	0 ,
1.23.	2,	5 .
r 3,
1.24. x 3,	1,	3 , p 2,				1,		0 , q 1,			0,		1 , r 4,			2,	1 .
1.25.x 1,	7,	0 , p 0,					3,	1 ,q 1,			1,			2 ,r 2,		1,			0 .
									8

1.26.x 11,	1,		4 , p 1,		1,		2 ,q 3,		2,	0	,r 1,	1,	1 .
x 13, 2,			18 , p 1,			1,	4 , q 3,			0,	2 ,
1.27.	2, 1 .
r 1,
1.28.x 0,	8,		9 , p 0,		2,		1 , q 3,		1,	1 , r 4,		0,	1 .
x 8,	7,		13 , p 0, 1,				5 , q 3,		1,		2 ,
1.29.	0,	1 .
r 1,
1.30. x 2,	7,	5 ,		p 1,	0,	1 ,q 1,		2,		0 ,r 0, 3,		1 .
x 15,	20,			1 , p 0,			2, 1 , q 0,			1,	1 ,
1.31.	3,		2 .
r 5,

Задача 2. Коллинеарны ли векторы c1 и c2 , построенные по век-

торам a и b?

2.1. a		1,	2,		,	b				3,		0,					1		2a	4b,					c		2	3b a.
				3									1 ,			c
2.2. a		1,	0,			b		2,				3,			1		a 2b,				c		2		3a b.
				1 ,									5 ,		c
2.3. a		2,	4,			b				1,		2,		,			1		5a	3b,					c	2		2a b.
				1 ,									7			c
2.4. a		1,	2,		,	b					2,	1,			,				1								c	2	8a b.
				3									1					c 4a 3b,
2.5. a 3,			5,	4 ,		b 5,						9, 7 ,		c1			2a b,				c2				3a 2b.
2.6. a		1,	4,		,	b				1,		1,					1		a b,		c	2		4a 2b.
				2									1 ,		c
2.7. a		1,	2,		,	b				3,		1,		,			1		4a	2b,					c		2	b 2a.
				5									0			c
2.8. a		3,	4,			b					2,	1,					1		6a	3b,					c	2		b 2a.
				1 ,									1 ,			c
												9

2.9. a		2,		3,			,	b							1,	0,					1			3a 9b,						c		2		a 3b.
					2													5 ,			c
2.10. a 1,				4,	2 ,			b 3,								2,		6 ,			c1 2a b,							c2					3b 6a.
2.11. a			5,	0,				b				7,				2,			,		1	2a b,			c		2			3b 6a.
					1 ,													3			c
2.12. a			0,	3,		,		b				1,				2,					1		5a 2b,					c			2		3a 5b.
					2													1 ,			c
2.13. a 2,				7,	1		, b 3,									5,		2 ,			c1 2a 3b,							c2					3a 2b.
2.14. a			3,	7,			b			1,					3,						1					c				2			b 2a.
					0 ,													4 ,			c 4a 2b,
2.15. a			1,	2,				b						2,		7,					,		1									c		2	b 3a.
					1 ,														1			c		6a 2b,
2.16. a			7,	9,		,		b					5,			4,			,		1	4a b,			c			2		4b a.
					2													3			c
2.17. a			5,	0,		,		b				6,				4,			,		1	5a 3b,					c			2			6b 10a.
					2													3			c
2.18. a			8,	3,				b				4,				1,					1				c	2			2b 4a.
					1 ,													3 ,		c 2a b,
2.19. a			3,	1,		,		b				5,				7,				,	1		4a 2b,							c		2		b 2a.
					6													10			c
2.20. a			1,	2,		,		b				7,				3,					1					c			2			b 2a.
					4													5 ,			c 6a 3b,
2.21. a			3,	7,			b				4,				6,						1	3a 2b,					c			2			5a 7b.
					0 ,												1 ,				c
2.22. a 2,				1,	4 ,		b 3,								7,			6 , c1					2a 3b, c2								3a 2b.
2.23. a 5,				1,	2		,	b 6,								0,		7 ,			c1 3a 2b,									c2				4b 6a.
2.24. a			9,	5,		,		b				7,				1,				,	1			2a b,			c			2			3a 5b.
					3													2			c
2.25. a			4,	2,			b				0,				1,				,		1	4b 3a,					c			2			4a 3b.
					9 ,													3			c
2.26. a			2,	1,		,		b				1,				3,				,	1			5a 2b,						c		2		2a 5b.
					6													8			c
																10