Функция распределения и ее свойства Дифференциальная функция распределения

Введем в рассмотрение функцию распределения

(24)

- вероятность того, что случайная величина Хпримет значение меньшее, чемx. Справедливы следующиесвойства функции распределения:

1. .

2. ,

если , т.е. вероятность попадания случайной величиныХв заданный интервал отaдоbравна разности значений функции распределения на концах этого интервала.

3.

если х₁  х₂, т.е. функция распределения является неубывающей от своего аргумента.

Определение. Случайная величина называетсянепрерывной, если ее функция распределения почти всюду дифференцируема. (Мы будем считать, что она дифференцируема везде, за исключением разве что конечного числа точек.) Производную от функции распределения называютдифференциальной функцией распределенияилиплотностью вероятности

(25)

Свойства дифференциальной функции распределения вытекают из соответствующих свойств функции распределения:

1. 

2. 

Вероятность попадания случайной величины в интервал от α доβ равна определенному интегралу от дифференциальной функции распределения.

3.

как производная от неубывающей функции.

Определение.Математическим ожиданиемM(X)непрерывной случайной величиныXназывается

(26)

Дисперсией называется математическое ожидание от квадрата отклонения с.в. от ее математического ожидания:

(27)

Справедлива формула для вычисления дисперсии:

(28)

Дисперсия равна математическому ожиданию от квадрата случайной величины без квадрата математического ожидания.

Пример 22.Случайная величина задана следующей функцией распределения:

Требуются найти параметр а, математическое ожидание и дисперсию.

Решение. Вычислим дифференциальную функцию распределения:

Далее,

откуда

Математическое ожидание и дисперсия случайной величины

Пример 23. Определить математическое ожиданиеM(X)случайной величиныX, дисперсиюD(X) по графику функции распределенияy=F(x):

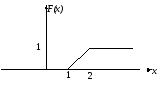
Решение. Запишем функцию распределения

Тогда плотность вероятности имеет вид

По определению математического ожидания и дисперсии имеем

Пример24. Случайная величинараспределена по показательному закону. По результатам наблюдаемых значений: 15, 15, 25, 10, 35 определить параметр

Решение. Если случайная величина распределена по показательному закону, то ее математическое ожиданиеВ свою очередь,среднее значение случайной величины. Тогда

Пример25. Случайная величина имеет плотность вероятности

Определить математическое ожидание случайной величины.

Решение. Если случайная величина распределена по показательному закону, то ее математическое ожиданиеСледовательно,

Нормальный закон распределения

Случайная величина называется распределенной по нормальному закону (нормальная с.в.), если ее дифференциальная функция распределения имеет следующий вид:

(29)

Математическое ожидание и дисперсиянормальной случайной величины соответственно равныа и:

;

Величина называетсясредним квадратичным отклонением. Введем в рассмотрениефункцию Лапласа:

(30)

Известны следующие свойства функции Лапласа:

1. 

т.е. функция Лапласа является нечетной функцией;

2. 

если x₁ < x₂, т.е. функция Лапласа – монотонно возрастающая функция;

3. .

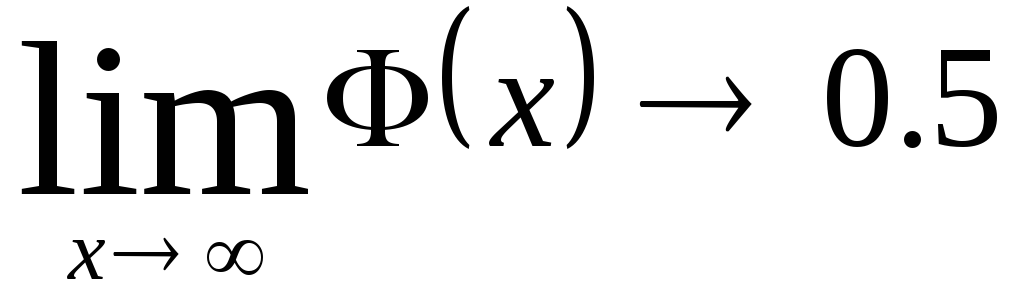Значения функции Лапласа находят при помощи таблиц, причем при x > 5 (иногда и приx >3) полагают.

Вероятность попадания нормального распределения с.в. в интервал от довычисляется с помощью функции Лапласа по формуле

(31)

Вероятность отклонения нормального распределения случайной величины от ее математического ожидания меньше чем на равна:

(32)

Пример 26. Случайная величинараспределена по нормальному закону. По результатам наблюдаемых значений: 35, 15, 5, 25, 5 – оценить параметр распределенияa.

Решение. Параметрaнормального распределения имеет смысл математического ожидания, которое, в свою очередь, равно среднему значению случайной величины, следовательно,

Пример27. Случайная величинаимеет плотность вероятности

Вычислить:

Решение. Математическое ожиданиеслучайной величины равно 3, среднее квадратичное отклонениеравно 2, следовательно, дисперсияТогда, пользуясь свойствами математического ожидания и дисперсии, получим