Методические указания к выполнению контрольной работы

Задача №1

Найти максимальное значение целевой функции f(x₁,x₂)=16x₁+9x₂ при ограничениях: ,x₁, x₂  0, x₁ и x₂ - целые числа.

Для решения использовать метод Гомори (метод отсечений), дать геометрическую интерпретацию решения задачи.

РЕШЕНИЕ

Это задача целочисленного программирования. Ее решение методом отсечений распадается на несколько этапов. Первоначально необходимо решить задачу линейного программирования (ЛП) без учета целочисленности переменных. Такая задача решается стандартным симплекс-методом. Для применения симплекс-метода необходимо записать задачу ЛП в канонической форме. Добавим в левую часть ограничений-неравенств неотрицательные переменные x₃, x₄ для того, чтобы ограничения можно было представить в виде точных равенств, тогда

f=16x₁+9x₂  max

, x₁ 0, x₂ 0, x₃ 0, x₄  0. Обозначим через

вектор-столбец переменных. В дальнейшем будем его записывать в транспонированном виде X^T=(x₁ x₂ x₃ x₄). Начальная таблица симплекс-метода и ее дальнейшие преобразования приводятся ниже.

		
0)	f	x1	x2	x3	x4	B
f-строка	1	-16	-9	0	0	0
	0	5	2	1	0	20	X0^T=(0 0 20 6)
	0	1	1	0	1	6
			
1)	f	x1	x2	x3	x4	B
f-строка	1	0	-13/5	16/5	0	64
	0	1	2/5	1/5	0	4	X1^T=(4 0 0 2)
	0	0	3/5	-1/5	1	2
2)	f	x1	x2	x3	x4	B
f-строка	1	0	0	7/3	13/3	218/3
	0	1	0	1/3	-2/3	8/3	X2^T=(8/3 10/3 0 0)
	0	0	3	-1	5	10

В приведенных таблицах стрелками указаны разрешающие столбцы и строки. Первоначальный план X₀^T=(0 0 20 6) есть неотрицательное базисное решение, которое не является оптимальным. На это указывают отрицательные элементы в f-строке. Также не оптимален план X₁^T=(4 0 0 2). Последний из полученных планов X₂^T=(8/3 10/3 0 0) является оптимальным – в f-строке нет отрицательных элементов. Однако, этот план не удовлетворяет условию целочисленности переменных. Графически этот план соответствует точке пересечения сплошных линий L1 и L2 с координатами (8/3, 10/3) приведенного ниже рисунка.

Так как полученное решение нецелочисленное, то в соответствии с методом Гомори, к ограничениям задачи необходимо добавить еще одно ограничение, которое отсекает полученный план и не должно отсекать ни одного целочисленного решения задачи. Такое ограничение называют правильным отсечением. Его строят по наибольшей дробной части нецелочисленных базисных переменных. Наибольшая дробная часть - у переменнойx₁. Если перейти от последней таблицы к соответствующим ей уравнениям, то получим следующее выражение для базисных переменных через свободные:

Правильное отсечение таково:

.

Фигурными скобками обозначают дробную часть заключенного в них выражения. Выделив дробную часть, придем к следующему неравенству:

.

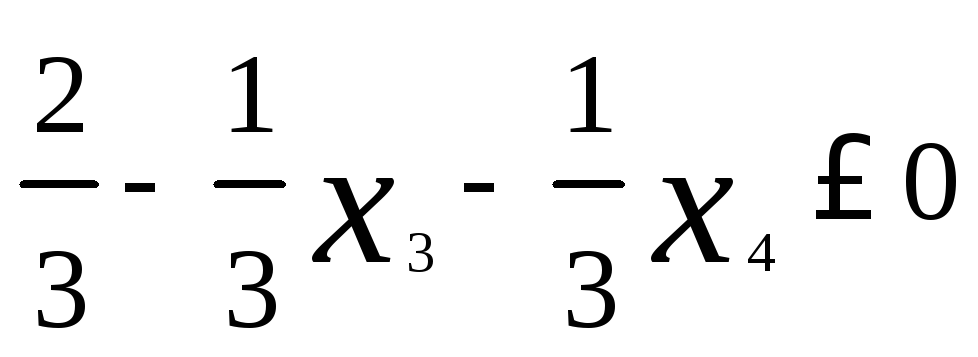Если в этом неравенстве переменные x₃ и x₄ выразить, используя полученные выше уравнения, через x₁ и x₂, то получится следующее ограничение:

2x₁+ x₂  8 .

На рисунке оно отсекает от области допустимых планов часть, содержащую найденное нецелочисленное решение, и вместе с тем, отсекаемый треугольник не содержит ни одного целочисленного плана. Графически граница этой области представлена пунктирной линией L3. Точка пересечения этой линии со сплошной линией L2 и дает искомое целочисленное решение.

В канонической форме правильное отсечение примет вид:

или .

Добавим это ограничение к последней из полученных в ходе симплекс-метода таблиц. Число базисных переменных при этом увеличится на единицу.

Введение в базис переменной x₃ приводит к следующему неотрицательному базисному решению:

				
3)	f	x1	x2	x3	x4	x5	B
f-строка	1	0	0	7/3	13/3	0	218/3
	0	1	0	1/3	-2/3	0	8/3
	0	0	1	-1/3	5/3	0	10/3
	0	0	0	1/3	1/3	-1	2/3
4)	f	x1	x2	x3	x4	x5	B
f-строка	1	0	0	0	2	7	68
	0	1	0	0	1	1	2	X4^T=(2 4 2 0 0)
	0	0	1	0	2	-1	4
	0	0	0	1	1	-3	2

Так как в f-строке нет отрицательных элементов, то полученное решение X₄^T=(2 4 2 0 0) является оптимальным. Оно также удовлетворяет и условию целочисленности и, следовательно, значения переменных x₁=2, x₂=4 дают решение исходной задачи.

ОТВЕТ: Максимальное значение целевой функции f(x₁,x₂)=16x₁+9x₂ при заданных ограничениях и целочисленных значениях переменных равно 68 и достигается при x₁=2, x₂=4.

Задача №2

Найти оптимальный план перевозок транспортной задачи, заданной таблицей:

		Пункты назначения				Запасы груза аi
		В1	В2	В3	В4
Пункты отправления	А1	14	28	21	28	270
	А2	10	17	15	24	200
	А3	14	30	25	21	430
Потребности в грузе bj		330	130	270	170

РЕШЕНИЕ

В таблице указаны поставщики груза А₁, А₂, А₃ и запасы груза у них, потребители грузаВ_1, В_2, В_3, В₄ и их потребности в грузе. Отметим, что суммарные потребности в грузе равны его суммарным запасам (900 некоторых условных единиц груза). В таблице на пересеченииi-той строки иj-того столбца приводится стоимость перевозки единицы груза из пунктаА_i в пункт В_j (элементы матрицы тарифов (с_ij)_mn). Решение задачи заключается в отыскании такого плана перевозок (матрицы перевозок Х), при котором все потребности в грузе будут удовлетворены, весь груз вывезен, и суммарная стоимость перевозки груза будет наименьшей.

Первоначально необходимо получить какой-либо допустимый базисный план перевозок. В невырожденном случае матрица перевозок базисного плана содержит (m+n-1) отличных от нуля элементов, соответствующих базисным переменным при решении такой задачи линейного программирования симплекс-методом. Для нахождения базисного плана перевозок можно использовать метод северо-западного угла, метод минимального элемента, метод Фогеля. Мы воспользуемся методом Фогеля, так как этот метод позволяет получить базисный план перевозок, близкий к оптимальному или даже оптимальнй.

При нахождении базисного плана перевозок методом Фогеля руководствуются следующим алгоритмом:

1. По каждой строке и каждому столбцу определяют разность между двумя наименьшими тарифами и записывают ее в дополнительные к исходной таблице строки и столбцы.

2. Из полученных разностей выбирают наибольшую и отмечают ее (ниже в таблице выделена жирным шрифтом).

3. В строке или в столбце, где имеется наибольшая разность, выбирается клетка с наименьшим тарифом с_ij и загружается наибольшей возможной перевозкой х_ij=min(а_i, b_j).

4. Производится перерасчет запасов и заявок на груз. Клетки, соответствующие тарифам, по которым уже невозможно что-либо перевезти, прочеркиваются, что соответствует нулевым значениям матрицы перевозок.

5. Пункты 1-4 выполняются до тех пор, пока вся таблица не будет заполнена элементами матрицы перевозок.

Применение метода Фогеля к нашей задаче приводит к следующей таблице:

		Пункты назначения				Запасы груза аi		Номер шага
		В1	В2	В3	В4			1	2	3	4
Пункты отправления	А1	14 -	28 -	21 200	28 70	270, 70, 0		7	7	7	7
	А2	10 -	17 130	15 70	24 -	200, 70, 0		5	5	9
	А3	14 330	30 -	25 -	21 100	430, 100, 0		7	7	4	4
Потреб-ности в грузе bj		330, 0	130, 0	270, 200, 0	170, 0
Номер шага	1	4	11	6	3
	2	4		6	3
	3			6	3
	4			4	7

В исходную таблицу, помимо тарифов, обозначенных курсивом, внесены соответствующие элементы матрицы перевозок, выделенные жирным шрифтом. Полученный базисный план перевозок может быть представлен следующей матрицей перевозок .

Отметим, что число отличных от нуля элементов матрицы перевозок равно (m+n-1)=3+4-1=6. Общая стоимость перевозки груза по полученному плану равна сумме произведений объемов перевозок между пунктами А_i и B_j на соответствующие тарифы:

Стоимость перевозок приводится в некоторых условных единицах.

Является ли полученный план перевозок оптимальным? Для ответа на этот вопрос используется метод потенциалов. Каждому из пунктов отправления и назначения грузов ставится в соответствие некоторое число – потенциал. Потенциалу может быть придан экономический смысл цены единицы груза в пункте его отправления и в пункте назначения. Будем обозначать потенциалы пунктов отправления U_i, а пунктов назначения - V_j. Их разность равна для заполненных ненулевыми перевозками клеток таблицы (x_ij0) соответствующему тарифу: V_j- U_i= с_ij. Это равенство позволяет получить систему из шести уравнений для определения потенциалов.

Однако неизвестных потенциалов семь. Обычно один из потенциалов полагают равным нулю. Пусть V₁=0, тогда решение системы уравнений таково:

.

Необходимым и достаточным критерием оптимальности полученного плана перевозок является выполнение условия V_j- U_i с_ij при x_ij=0 (и V_j- U_i= с_ij при x_ij0). Для проверки этого условия в рассматриваемой задаче выпишем еще раз таблицу, соответствующую матрице тарифов, дополнив ее потенциалами пунктов отправления и пунктов назначения груза и разностью потенциалов V_j- U_i= _ij.

		Потенциалы Vj
		V1=0	V2=2	V3=0	V4=7
Потенциалы Ui	U1=-21	14 - 21 +	28 - 23	21 200 21	28 70 28 -
	U2=-15	10 - 15	17 130 17	15 70 15	24 - 22
	U3=-14	14 330 14 -	30 - 16	25 - 14	21 100 21 +

Разность потенциалов указана в левом нижнем углу клеток таблицы. Из таблицы видно, что для выделенных клеток (1,1) и (2,1) условие оптимальности плана перевозок не выполняется, то есть полученный план не является оптимальным. Его необходимо «улучшить». Для этого составим цикл перераспределения поставок. Первая вершина этого цикла расположена в клетке, где нарушено условие оптимальности плана перевозок. В нашем случае таких клеток две (1,1) и (2,1). Из них выбираем ту, в которой разность (_ij-с_ij) является наибольшей. Так как (21-14) (15-10), то начальная вершина цикла расположена в клетке (1,1). Она обозначена знаком «+». Остальные вершины цикла располагаются в клетках таблицы, загруженных ненулевыми перевозками, причем ребра цикла могут располагаться только по строкам или столбцам таблицы. Единственный цикл, удовлетворяющий этим требованиям, имеет вершины в клетках (1,1), (1,4), (4,3) и (3,1), он и показан в таблице. Каждой вершине цикла, начиная с первой, поочередно присваиваются знаки «+» и «-». В нашей задаче знак «-» присвоен вершинам, находящимся в клетках (1,4) и (3,1); поставки перераспределяются на величину

=min(70, 330)=70 - наименьшую из перевозок в клетках, отмеченных знаком

«-». В вершинах цикла со знаком «+» величина прибавляется к существующей перевозке, а в вершинах цикла со знаком «-» - вычитается. Измененная таким образом матрица перевозок принимает вид: .

В перевозки включена клетка таблицы (1,1) и исключена перевозка, соответствующая клетке (1,4).Отметим, что полученная матрица перевозок, как и прежняя, также содержит (m+n-1)=3+4-1=6 отличных от нуля элементов. Стоимость перевозки груза по этому плану составит

, что

меньше, чем стоимость перевозки по предыдущему плану.

Для установления оптимальности этого плана необходимо снова найти потенциалы пунктов отправления и пунктов назначения, соответствующие вновь полученному плану. Для заполненных ненулевыми перевозками клеток таблицы (x_ij0) запишем уравнения: V_j- U_i= с_ij для нахождения потенциалов. Вновь получим систему из шести уравнений с семью неизвестными потенциалами:

одно из ее решений таково .

Снова проверим выполнение условия оптимальности полученного плана перевозок (V_j- U_i с_ij при x_ij=0). Выпишем еще раз таблицу матрицы тарифов, дополнив ее потенциалами пунктов отправления и пунктов назначения груза и разностью потенциалов V_j- U_i= _ij. (Величины _ij указаны в клетках таблицы слева внизу).

		Потенциалы Vj
		V1=0	V2=9	V3=7	V4=7
Потенциалы Ui	U1=-14	14 70 14	28 - 23	21 200 21	28 - 21
	U2=-8	10 - 8	17 130 17	15 70 15	24 - 15
	U3=-14	14 260 14	30 - 23	25 - 21	21 170 21

Из таблицы видно, что условия оптимальности плана перевозок

_ij =V_j-U_i с_ij при x_ij=0

_ij =V_j-U_i= с_ij при x_ij0

выполняются, то есть полученный план является оптимальным.

ОТВЕТ: матрица оптимального плана перевозок задачи имеет вид: .

Наименьшая стоимость перевозок в соответствии с данным планом составляет условных единиц.

ЗАМЕЧАНИЯ.

1. Оптимальных планов перевозок может быть несколько, а наименьшая стоимость принимает единственное значение.

2. Для придания полученным в ходе решения задачи потенциалам экономического смысла цены единицы груза в пунктах отправления и в пунктах назначения их необходимо увеличить на одно и то же постоянное число так, чтобы все потенциалы были положительны.

3. Для достижения оптимального плана перевозок может потребоваться неоднократное применение процедуры перераспределения поставок. В задачах контрольной работы аккуратное применение метода Фогеля, как правило, сразу приводит к оптимальному плану перевозок, в чем следует убедиться, применяя метод потенциалов.

Задача №3

Планируется на очередной год деятельность четырех предприятий, входящих в производственное объединение. Инвестиции в объеме 50 условных единиц могут быть распределены между предприятиями порциями, кратными 10 условным единицам.

Составить оптимальный план распределения капиталовложений между этими предприятиями, обеспечивающий максимальное увеличение прибыли производственного объединения. Зависимость прибыли для j-того предприятия -f_j(x) от объема сделанных капиталовложенийx приведена в таблице.

x	f1(x)	f2(x)	f3(x)	f4(x)
0	0	0	0	0
10	8	6	3	4
20	10	9	4	6
30	11	11	7	8
40	12	13	11	13
50	18	15	18	16

Задачу решить методом динамического программирования.

РЕШЕНИЕ

Составим математическую модель задачи. Обозначим через x_k количество средств, выделенныхk-тому предприятию. Суммарная прибыльZбудет равна

.

При условиях ,

x_k  0, x_k  {10, 20, 30, 40, 50}.

Ограничения линейные, но целевая функция Z нелинейна, так как функцииf_j(x) нелинейны. Такие задачи не могут решаться обычными методами линейного программирования. Для ее решения воспользуемся методом динамического программирования. Распределение средств между четырьмя предприятиями рассматриваем как четырехшаговый процесс, на каждом шаге которого выделяются средства (x_k) соответствующему предприятию. Обозначим черезs_kнераспределенные средства послеk-того шага. В трактовке динамического программирования производственное объединение понимается как управляемая система,x_k– управляющие воздействия на нее,s_k– параметры, характеризующие состояние системы. Ясно, что первоначальноs₀=50, а после четвертого шага все средства должны быть распределены - s₄=0. При произвольномk(0k4) оставшиеся нераспределенными послеk-того шага средстваs_kсвязаны с распределяемыми на этом шаге средствамиx_k и остатком средств после предыдущего шагаs_k-1очевидным соотношением:

s_k =s_k-1-x_k (k=1, 2, 3, 4).

В динамическом программировании подобные уравнения называют уравнениями состояния управляемой системы

Введем в рассмотрение - условно оптимальную прибыль, полученную отk-того, (k-1), …, 4-го предприятий, если между ними оптимально распределены средстваs_k-1(0 s_k-150). Из условия задачи следует, что величиныs_k-1кратны 10. Средстваx_k, распределяемые наk-том шаге, удовлетворяют условию 0 x_k s_k-1(либоk-тому предприятию ничего не выделяется, либо выделяется не более того, что имеется кk-тому шагу).

В соответствии с принципом оптимальности Беллмана, на каждом шаге нужно выделять средства x_kтак, чтобы в совокупности с оптимальным распределением на всех последующих шагах получить наибольшую суммарную прибыль. Применение принципа оптимальности на каждом шаге приводит к следующим уравнениям:

Это уравнения Беллмана для данной задачи. Последовательно решаем записанные уравнения, проводя условную оптимизацию на каждом шаге, начиная с последнего четвертого предприятия.

4 шаг. В таблице f₄(x)– возрастающая функция, поэтому все средства, оставшиеся к четвертому шагу необходимо для получения максимальной прибыли вложить в это четвертое предприятие, то есть

.

3 шаг. Решаем уравнение (b). Делаем все предположения об остатках средствs₂к третьему шагу.s₂может принимать значения 0, 10, 20, 30, 40, 50. В зависимости от этого выбираем 0 x₃ s₂, находимs₃ =s₂ -x₃и ищем максимум . Для каждогоs₂наибольшее из этих значений есть условно оптимальная прибыль, полученная при оптимальном распределении средствs₂третьим и четвертым предприятиями.

Решение получаем с помощью следующей расчетной таблицы для третьего шага условной оптимизации.

s2	0	10		20			30				40					50
x3	0	0	10	0	10	20	0	10	20	30	0	10	20	30	40	0	10	20	30	40	50
s3 =s2 -x3	0	10	0	20	10	0	30	20	10	0	40	30	20	10	0	50	40	30	20	10	0
f3(x3)	0	0	3	0	3	4	0	3	4	7	0	3	4	7	11	0	3	4	7	11	18
	0	4	3	6	7	4	8	9	8	7	13	11	10	11	11	16	16	12	13	15	18
	0	4		7			9				13					18
	0	0		10			10				0					50

2 шаг. Решение уравнения (c) проводится совершенно аналогично предыдущему и представлено следующей таблицей.

s1	0	10		20			30				40					50
x2	0	0	10	0	10	20	0	10	20	30	0	10	20	30	40	0	10	20	30	40	50
s2 =s1 -x2	0	10	0	20	10	0	30	20	10	0	40	30	20	10	0	50	40	30	20	10	0
f2(x2)	0	0	6	0	6	9	0	6	9	11	0	6	9	11	13	0	6	9	11	13	15
	0	4	6	7	10	9	9	13	13	11	13	15	16	15	13	18	19	18	18	12	15
	0	6		10			13				16					19
	0	10		10			10, 20				20					10

1 шаг. Решаем уравнение (d). Учитывая то обстоятельство, что все средства должны быть распределены полностью, расчетная таблица для этого шага будет иметь более простой вид:

s0	50
x1	0	10	20	30	40	50
s1 =s0 -x1	50	40	30	20	10	0
f1(x2)	0	8	10	11	12	18
	19	24	23	21	18	18
	24
	10

На шаге 1 условной оптимизации получаем у.е. Это и есть наибольшее значение прибыли производственного объединения

Z_max= 24 у.е. Оно достигается при

Для установления значений , при которых достигается наибольшее значение прибыли, воспользуемся уравнениями состояния. Из приведенных выше таблиц найдем - значения величин, соответствующие оптимальному распределению инвестиций (для удобства они выделены в таблицах жирным шрифтом). При этом совершаем шаги от первого предприятия к четвертому:

Приходим к следующему ответу:

Наибольшую прибыль Z_max=24 у.е. производственное объединение получит, если инвестиции между предприятиями распределены так:

первое предприятие получает ;

второе предприятие получает ;

третье предприятие получает ;

четвертое предприятие получает

Замечание.

Последовательность распределения средств между предприятиями может быть выбрана и иной, однако ответ получится такой же.

Задача №4

В сети, заданной перечислением своих дуг, узлов и расстояний между узлами, установить кратчайшие маршруты из всех узлов в узел 1 и определить их длину.

Номер дуги	Имя дуги	Началь-ный узел	Конеч-ный узел	Рассто-яние (dij)
1	C21	2	1	2
2	C31	3	1	4
3	C41	4	1	10
4	C42	4	2	11
5	C52	5	2	5
6	C43	4	3	3
7	C63	6	3	1
8	C54	5	4	8
9	C64	6	4	7
10	C75	7	5	6
11	C76	7	6	9

РЕШЕНИЕ

Из условия задачи ясно, что сеть состоит из семи узлов и одиннадцати соединяющих их дуг. Изобразим заданную сеть графически так, чтобы избежать пересечения дуг вне узлов сети. Узлы сети изображаем пронумерованными кружками, а дуги – стрелками с указанием длины дуги. Отметим, что сеть не имеет циклов, поскольку идя по дугам в направлении стрелок нельзя вернуться в вершину, из которой начат маршрут. В этой сети узел 7 является начальным, а узел 1 – конечным (рис. 1).

u₂=2

u₅=7

5

1

3

4

2

10

6

11

8

9

7

u₁=0

u₄=7

u₇=13

u₃=4

u₆=5

Рисунок 1.

Ясно, что длины кратчайших маршрутов из узла jв узел 1 и из узла 1 в узелjодинаковы (а последовательности узлов маршрутов взаимно обратны). Будем определять кратчайшие расстояния от узла 1 до каждого из узлов сетиj(т.е. следовать против направления стрелок).

Введем следующие обозначения:

d_ij– расстояние между смежными узламиiиj(длина дугиC_ij).

u_j– кратчайшее расстояние между узлами 1 иj,u₁= 0.

Общая формула для вычисления u_jимеет вид:

Кратчайшее расстояние u_jдо узлаjможно вычислить лишь после того, как определено кратчайшее расстояние докаждогопредыдущего узлаi, соединенного дугой с узломj.

Вычисления заключаются в последовательном поэтапном применении приведенной выше формулы.

Этап 1: u₁=0.

Этап 2: u₂ =u₁+d₁₂ = 0+2 = 2 (из 1),

u₃ =u₁+d₁₃ = 0+4 = 4 (из 1).

Этап 3: u₄ =min{u₁+d₁₄,u₂+d₂₄,u₃+d₃₄} =min{0+10, 2+11, 4+3}=7 (из 3). Этап 4:u₅ =min{u₂+d₂₅,u₄+d₄₅} =min{2+5, 7+8}=7 (из 2),

u₆ =min{u₃+d₃₆,u₄+d₄₆} =min{4+1, 7+7}=5 (из 3).

Этап 5: u₇ =min{u₅+d₅₇,u₆+d₆₇} =min{7+6, 5+9}=13 (из 5).

Найденные минимальные расстояния u_jуказаны на графическом изображении сети. Проделанные выкладки позволяют сформулировать ответ.

Кратчайшие маршруты из каждого узла jсети в узел 1 и их длиныu_j таковы:

2 1,u₂ = 2;

3 1,u₃ = 4;

4 31,u₄ = 7;

5 21,u₅ = 7;

6 31,u₆ = 5;

7521,u₇ = 13.