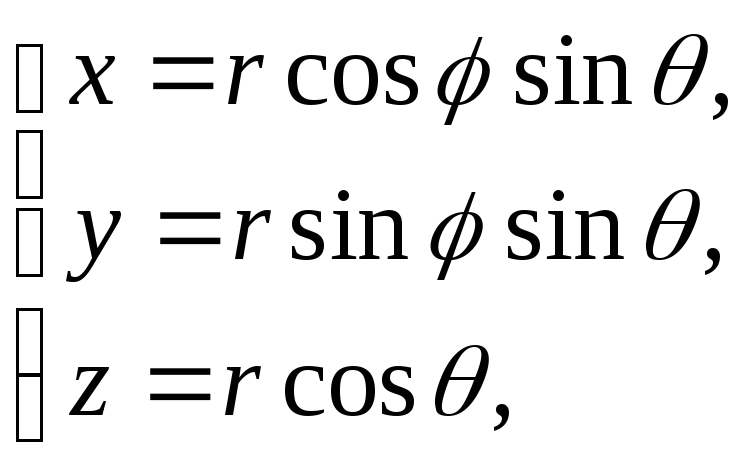Решение типовых примеров

1. Привести уравнения данных гармонических колебаний

к виду

.

Найти амплитуду А, фазу , период гармоники и построить ее график.

Решение. Привести уравнения данных гармонических колебаний

к виду , где– амплитуда,,и– период колебания.

В нашем случае:

, и,, откудапринадлежит 4 четверти и,. Тогда

,.

От графика функции перейдем к графику функциис помощью следующей цепочки преобразований:

то есть к нашей функции .

Построение:

1. Строим одну волну синусоиды .

2. Строим график функции , которая имеет период (то есть сжимаем функциюв три раза).

3. Увеличивая ординаты графикав 5 раз, получаем график функции.

4. Сдвигаем график функции на 12,3⁰ вправо вдоль оси Ох.

у

5

1

120⁰132,3⁰

0 12,3⁰60⁰180⁰360⁰х

у₂=sin3xу₁=sinx

у₃=5sin3x у=5sin(x–12,3⁰)

Рисунок 1

2. Даны векторы и . Показать, что векторыобразуют базис трехмерного пространства, найти разложение и координаты векторав этом базисе. Полученную систему линейных уравнений решить тремя методами:

а) через определители (формулы Крамера),

б) через обратную матрицу,

в) методом Гаусса (через расширенную матрицу).

Решение. Составим определитель из координат векторов и вычислим его, разложив по элементам первой строки:

значит, векторы образуют базис трехмерного пространства и векторможно разложить по векторам базиса

,

где ,,– координаты векторав базисе.

Перейдем к матричной записи полученного векторного уравнения

Используя свойства матриц и действия над ними, получим систему линейных уравнений относительно неизвестных ,,:

а) Решение полученной системы линейных уравнений через определители.

Находим главный определитель системы уравнений:

следовательно, данная система уравнений имеет единственное решение, которое находим по формулам Крамера:

где получается путем заменыi-го столбца свободными членами.

Вычислим определители .

.

Находим

Ответ:

б) Решение системы через обратную матрицу.

Обозначим через А матрицу коэффициентов при неизвестных, Х – матрицу-столбец неизвестных Х₁, Х₂, Х₃; Н – матрицу-столбец свободных членов:

С учетом этих обозначений данная система уравнений принимает следующую матричную форму:

.

Для нахождения решения системы уравнений необходимо вычислить обратную матрицу

,

где – алгебраическое дополнение элемента.

Вычислим определитель и алгебраические дополнения элементов матрицы А.

следовательно, матрицаА имеет обратную матрицу .

Тогда

.

Решение системы уравнений

Отсюда

Ответ:

в) Решение системы линейных уравнений методом Гаусса (через расширенную матрицу).

Составим расширенную матрицу данной системы линейных уравнений и с помощью элементарных преобразований матрицы приведем ее к треугольному виду (ниже главной диагонали все элементы равны нулю).

Видим, что ранги матриц А и В совпадают и равны числу неизвестных, то есть . Следовательно, система линейных уравнений имеет единственное решение. Чтобы найти это решение, перейдем от матричной записи к ступенчатой системе уравнений.

Двигаясь снизу вверх (обратный ход метода Гаусса), получаем . Полученный результат подставляем во второе уравнение, а потом вместе с найденнымв первое уравнение:

Ответ:

3. Определить тип кривой , найти ее параметры; определить угловой коэффициент прямой . Найти точки пересечения данных линий и сделать чертеж.

Решение. Приведем уравнение кривой к каноническому виду , разделив на 225. Получим уравнение эллипса . Его большая полуось , малая полуось. Центр совпадает с началом координат.

Уравнение прямой имеет вид «в отрезках», что удобно для построения. Для нахождения углового коэффициента прямой приведем ее к виду, выразиву через х: .

Угловой коэффициент .

Для нахождения точек пересечения этих линий решим систему

Возведем второе уравнение в квадрат

и подставим в первое уравнение:

Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.

у

3

–5 0 5 х

–3

Рисунок 2

4. Даны координаты вершин пирамиды АВСD:

Требуется:

1) записать векторы в системе орти найти модули этих векторов;

2) найти угол между векторами и ;

3) найти проекцию вектора на вектор ;

4) найти площадь грани АВС;

5) найти объем пирамиды АВСD;

6) составить уравнение ребра АС;

7) составить уравнение грани АВС.

Решение.

1) Произвольный вектор представляется в системе ортпо формуле

,

где – координаты вектора. Если заданы точки,, то для вектора

,

то есть

.

Воспользовавшись формулой и координатами заданных точек А, В, С, D, получим:

;

;

.

Если вектор , то его модуль вычисляется по формуле:.

Модули найденных векторов

;

;

.

2) Известна формула

,

где – скалярное произведение векторов и, которое можно вычислить следующим образом:

.

У нас

,

то есть .

3) Известно, что ,

то есть в нашем случае

.

4) Воспользуемся формулой нахождения площади треугольника, построенного на векторах и

,

где – векторное произведение векторов, которое можно вычислить по следующему правилу:

.

В нашем примере , причем

.

Таким образом, (кв. ед.).

5) Объем пирамиды, построенной на трех некомпланарных векторах можно найти по формуле

,

где – смешанное произведение векторов, которое вычисляется следующим образом:

.

У нас , где

,

то есть (куб. ед.).

6) Известно, что уравнение прямой, проходящей через две заданные точки и, имеет вид:

.

Подставив координаты точек А и С, получим:

,

то есть уравнение ребра АС окончательно запишется следующим образом:

или.

7) Уравнение плоскости, проходящей через три заданные точки ,,, можно записать в виде

.

Подставляя в него координаты точек А, В, С, получим:

5. Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х:

Требуется:

1) найти точки разрыва функции, если они существуют;

2) найти односторонние пределы и скачок функции в точках разрыва;

3) сделать чертеж.

Решение. Данная функция опреелена и непрерывна в интервалах . Приименяется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.

Определим односторонние пределы в точке :

Односторонние пределы совпадают. Функция в этой точке непрерывна.

Определим односторонние пределы в точке :

Так как односторонние пределы функции у в точке не равны между собой, то в этой точке функция имеет разрыв первого рода.

Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке скачок функции

Построим график функции.

у

0 х

Рисунок 3

6. Провести полное исследование функции методами дифференциального исчисления и построить ее график.

Решение.

1) Область определения функции

.

2) Исследование на непрерывность и классификация точек разрыва.

Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:

Таким образом, точка х = 4 является для заданной функции точкой разрыва второго рода, а прямая х = 4 – вертикальной асимптотой графика.

3) Исследование на экстремум и промежутки монотонности.

х		–2	(–2; 4)	4	(4; 10)	10
	+	+	–	не сущ.	–	0	+
		max				min

.

4) Исследование графика на выпуклость, вогнутость, точки перегиба.

Так как , то график заданной функции точек перегиба не имеет. Остается выяснить вопрос об интервалах его выпуклости и вогнутости:

х		4
	–	не сущ.	+

5) Исследование графика на наличие наклонных асимптот.

Таким образом, прямая – наклонная асимптота графика.

6) График заданной функции пересекает ось Оу в точке (0; –5).

По результатам исследования строим график.

у

20

4

–4 0 4 х

Рисунок 4

7. а) Решить систему двух линейных уравнений в области комплексных чисел по формулам Крамера. Найденные изобразить на комплексной плоскости;, записать в показательной и тригонометрической формах; найти, записать в показательной и алгебраической формах и изобразить геометрически.

Решение. Найдем решение системы линейных уравнений по формулам Крамера . Для этого вычислим главный определитель системыи определители, учитывая, что– комплексное число, где.

Находим :

(т.к.);

Таким образом, решение данной системы уравнений в алгебраической форме записи:

в векторной форме записи

Для того, чтобы найти в алгебраической форме, складываем действительные и мнимые части чисел:

.

Вектор, соответствующий числу , строим как сумму векторов по правилу параллелограмма.

Для того, чтобы найти в алгебраической форме, вычитаем действительные и мнимые части чисел:

.

Вектор, соответствующий числу , записываем как сумму векторови, строим его по правилу параллелограмма.

у

–3,5 z₂

j

– z₂–2 0 3,5 x

z₁z

и

Рисунок 5

Найдем модуль и аргументкомплексных чисел( или ;в 1 и 4 четвертях; во 2 и 3 четвертях, знак «+» или «–» выбираем так, чтобы аргумент был наименьшим по модулю).

Число принадлежит 3 четверти:

(аргумент );

(модуль ).

Число принадлежит 1 четверти:

;

Запишем числа в показательнойи тригонометрическойформах:

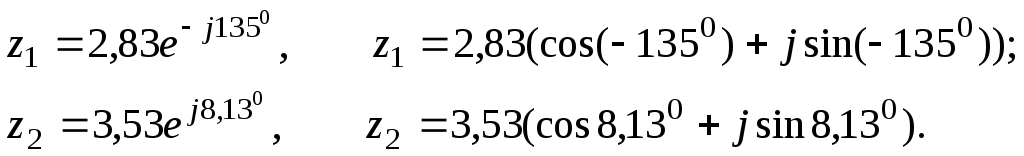
так как при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

так как при делении комплексных чисел их модули делятся, а аргументы вычитаются.

Найдем , используя формулу

, гдет = 0, 1, 2, …, п – 1.

В нашем примере п = 6, т = 0, 1, 2, 3, 4, 5 и мы получим 6 различных значений корня:

при т = 0

при т = 1

при т = 2

при т = 3

при т = 4

при т = 5

у

w₃

w₄96⁰w₂

156⁰36⁰

0 –24⁰x

–144⁰–84⁰w₁

w₅

w₆

Рисунок 6

.

7. б) Найти скорость (м/с) и ускорениеа (м/с²) материальной точки, траектория которой задана параметрическими уравнениями

в момент времени с.

Решение. Вектор есть радиус-вектор движущейся материальной точки. В нашем случае. Найдем уравнение траектории (годографа) движущейся материальной точки.

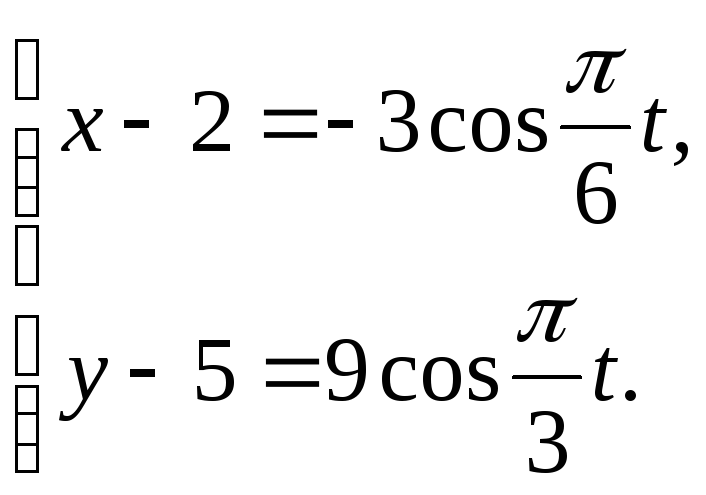
В первом уравнении обе части возведем в квадрат

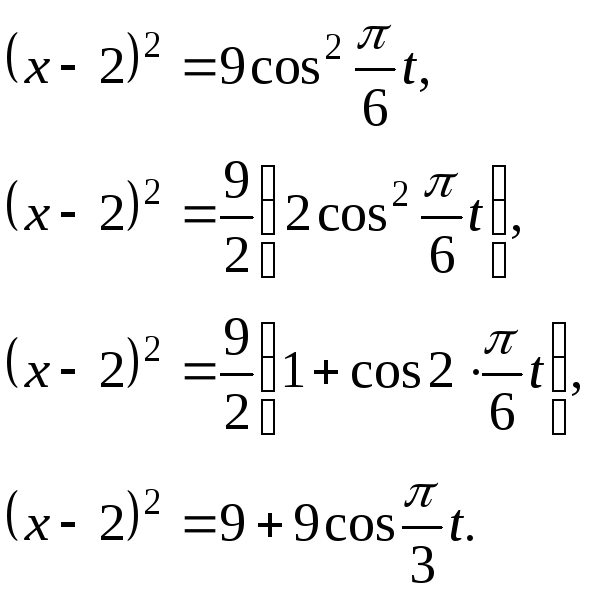
Система уравнений примет вид

Исключая , получим уравнение

Это есть уравнение параболы с вершиной с осью, параллельной осиОу, параметром и ветви направлены вверх. Координаты точкив момент временис будут

т.е. .

Построим полученную траекторию.

у

14 М₀(5; 14)

4

0 2 5 х

–4 А

Рисунок 7

Вектор есть вектор скорости материальной точки, который направлен по касательной к годографу данной линии в данной точке. В нашем случае

или

В момент времени с скорость материальной точки равна

или

а величина скорости м/с.

Как известно, вектор ускорения движения материальной точки равен

В нашей задаче

и

. Отметим этот вектор на чертеже.

м/с².

Ответ: В момент времени с величина скорости точким/с, а ускорением/с².

7. в) Найти скорость (м/с) и ускорениеа (м/с²) материальной точки, траектория которой задана параметрическими уравнениями

в момент времени с.

Решение. Вектор есть радиус-вектор движущейся материальной точки. В нашем случае. Найдем уравнение траектории (годографа) движущейся материальной точки.

Обе части уравнений возведем в квадрат и почленно сложим.

Получили уравнение эллипса с центром в точке и полуосями. Координаты точкив момент временис будут

у

В₁

–2 0 х

–3

А₂О 'А₁

–12

Рисунок 8

Вектор есть вектор скорости материальной точки, который направлен по касательной к годографу данной линии в данной точке. В нашем случае

или

В момент времени с скорость материальной точки равна

,

(отметим этот вектор на чертеже),а величина скорости м/с.

Как известно, вектор ускорения движения материальной точки равен

В нашей задаче

или и

;

(отметим этот вектор на чертеже).

м/с².

Ответ: В момент времени с величина скорости точким/с, а ускорением/с².

8. а) Вычислить площадь фигуры, ограниченной заданными параболами .

Решение. Найдем абсциссы точек пересечения заданных парабол. Для этого приравняем правые части их уравнений:

.

Отсюда

.

у

1

–1 0 1 х

Рисунок 9

Площадь вычислим по формуле

,

где , – кривые, ограничивающие фигуру ().

В нашем случае

8. б) Найти объем тела, образованного вращением вокруг оси Ох фигуры, расположенной в первом квадранте и ограниченной заданными параболой , прямой и осью Ох.

Решение. Найдем абсциссу точки пересечения параболы и прямой в первом квадранте. Для этого решим уравнение

,

,

.

Первому квадранту соответствует корень .

Найдем теперь абсциссу точки пересечения прямой с осью Ох, решив уравнение , откуда.

Таким образом, можно считать, что тело вращения ограничено при поверхностью, образованной вращением параболывокруг осиОх, а при – вращением прямой.

у

8

0 2 х

Рисунок 10

Объем ищем по формуле .

.

Для вычисления второго интеграла используем подстановку . Тогдаи.

Отсюда

.

9. а) Вычислить длину дуги кривой, заданной параметрическими уравнениями

Решение. Длина дуги кривой, заданной параметрическими уравнениями, вычисляется по формуле

.

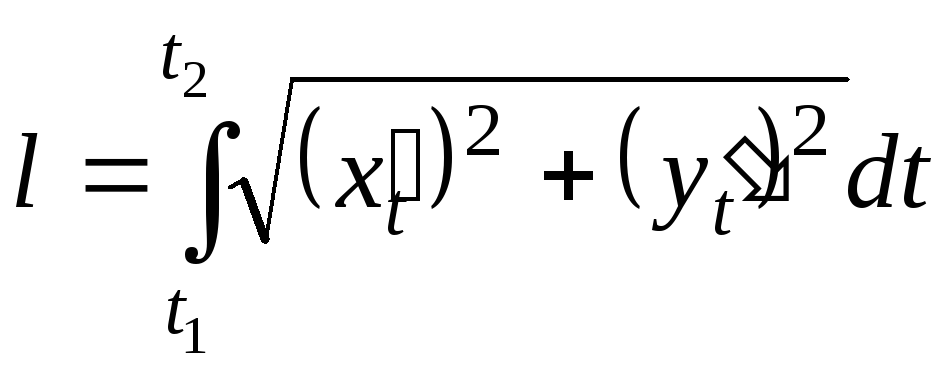Находим и для рассматриваемой кривой:

Вычислим длину дуги при :

ед.

Ответ: ед.

9. б) Вычислить площадь фигуры, ограниченной кривыми ,, заданными в полярной системе координат.

Решение. Площадь фигуры, ограниченной одной или двумя кривыми, заданными в полярной системе координат, вычисляется по формулам

или

.

Сделаем чертеж искомой площади, учитывая, что , поэтому, то есть.

p/2

6 p/3

4 p/6

0. r

Рисунок 11

, .

Так как фигура симметрична относительно прямой , то

=

10. Найти частное решение дифференциального уравнения второго порядка, допускающее понижение порядка, удовлетворяющее указанным начальным условиям

Решение. Данное дифференциальное уравнение второго порядка не содержит явно функцию у. Положим , гдер – некоторая функция аргумента х. Если , то, и данное уравнение примет вид. Мы получили уравнение первого порядка относительно переменныхр и х. Решим это уравнение:

, или.

Определим численное значение С₁ при указанных начальных условиях. Имеем . Следовательно,. Теперь решаем уравнение первого порядка:

Определим численное значение С₂ при указанных начальных условиях. Имеем .

Таким образом, есть частное решение, удовлетворяющее указанным начальным условиям.

11. Найти частное решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами , удовлетворяющее указанным начальным условиям.

Решение. Общее решение у данного уравнения равно сумме общего решения у_одн однородного уравнения и какого-либо частного решения данного уравнения, то есть

.

Для нахождения у_одн составим характеристическое уравнение , имеющее комплексные корни. В этом случае общее решение однородного уравнения ищем в виде

,

где – комплексные корни характеристического уравнения. Подставив, имеем:

.

Частное решение неоднородного дифференциального уравнения ищем в виде, так как правая часть неоднородного уравнения есть функцияи числаявляются корнями характеристического уравнения. Приимеем:

.

Дважды дифференцируя последнее равенство, находим :

.

Подставив в данное уравнение и, получим:

,

откуда . Следовательно,и

.

Найдем :

.

Используя начальные условия, получим систему

откуда .

Следовательно, есть искомое частное решение данного дифференциального уравнения.

12. Классическим методом и методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.

Решение. Решением этой системы является пара функций ,, удовлетворяющих системе, причем .

1) Классический метод решения.

Продифференцируем первое уравнение по переменной :

.

Из первого уравнения определяем , следовательно, из второго уравнения имеем

.

Подставляем в уравнение, полученное после дифференцирования, приходим к уравнению

,

– линейное дифференциальное уравнениеII порядка с

постоянными коэффициентами.

Составляем характеристическое уравнение и находим его корни:

– действительные различные корни.

В этом случае общее решение дифференциального уравнения имеет вид

,

.

Ранее определили . Тогда

.

Общее решение системы

Находим значения произвольных постоянных, используя начальные условия :

Частное решение системы

2) Метод операционного исчисления.

Пусть . По теореме о дифференцировании оригинала получим

Следовательно, операторная (изображающая) система имеет вид:

Из первого уравнения определяем и подставляем во второе уравнение:

, .

Представим дробь в виде суммы простых дробей:

Следовательно, .

По таблице изображений находим

.

Аналогично:

,

,

.

Частное решение системы

13. Найти область сходимости степенного ряда .

Решение. Введем новое переменное и получим ряд ,где и . Найдем радиус сходимости степенного ряда

Таким образом, интервал сходимости ряда (–3; 3), то есть .

Выясним вопрос о сходимости этого ряда на концах интервала.

При ряд принимает вид

.

Получили числовой знакочередующийся ряд, применим к нему признак Лейбница:

1) ,

2) , в самом деле,

Значит, ряд сходится и – точка сходимости ряда.

При получаем ряд. Сравним его с гармоническим рядом, который расходится. Применим предельный признак сравнения.

.

Значит, оба ряда ведут себя одинаково, то есть ряд расходится и– точка расходимости.

Таким образом, область сходимости для ряда

.

Перейдем к переменному х:

или .

Ответ: Область сходимости .

14. а) Найти разложение в степенной ряд по степеням х решения дифференциального уравнения (записать три первых, отличных от нуля, члена этого разложения).

Решение. Так как по условию , то искомое частное решениеможно записать в виде:

Из начальных условий уже известны и. Подставив эти значения в заданное уравнение, вычислим:

.

Последовательно дифференцируя данное уравнение, будем иметь:

Теперь вычислим значения производных при :

.

Следовательно, или

есть искомое частное решение.

14. б) Используя разложение подынтегральной функции в степенной ряд, вычислить интеграл с точностью до 0,001.

Решение. .

Разложим подынтегральную функцию в степенной ряд. Для этого используем ряд

,

где . Положими заменимх на :

Так как отрезок интегрирования принадлежит области сходимости полученного ряда, то будем интегрировать почленно в указанных пределах:

В полученном знакочередующемся ряде четвертый член по абсолютному значению меньше 0,001. Следовательно, требуемая точность будет обеспечена, если учитывать только первые три члена ряда.

.

15. Дана функция двух переменных . Найти:

1) экстремум функции ;

2) в точкеА(1; –2);

3) наибольшую скорость возрастания точкеА(1; –2).

Решение. 1) Для отыскания экстремума функции предварительно найдем частные производные первого и второго порядка:

Приравняем их к нулю и решим систему уравнений:

Решением системы является точка М(–4; 1). Точка М(–4; 1) называется подозрительной на экстремум. Найдем частные производные второго порядка в точке М:

Из них составим определитель второго порядка

Так как , то в точкеМ(–4; 1) есть экстремум. Производная , а, значит, это точка минимума функции.

.

2) Градиент функции найдем по формуле:

,

и были найдены в пункте 1.

.

Градиент функции в точкеА(1; –2):

.

3) Наибольшая скорость возрастания функции равна модулю градиента:

.

16. а) Найти объем тела, ограниченного параболоидом , цилиндром и плоскостью, через тройной интеграл, применяя цилиндрическую систему координат.

Решение. Сделаем чертеж, учитывая, что вершина параболоида находится в точке В(0; 0; 4), радиус окружности в плоскости хОу равен , осью цилиндраявляется осьОz, радиус поперечного сечения равен 2, а уравнение описывает координатную плоскостьхОу.

z

4 В

2 2у

3

х

Рисунок 12

Объем полученного тела найдем через тройной интеграл по формуле

.

С учетом характера области интегрирования вычисления удобно вести в цилиндрических координатах.

Зависимость между декартовыми и цилиндрическими координатами точки имеет вид:

где угол равен углу между осьюОх (х>0) и ,ии .

z М(j;r;z) rz 0 у j М¢ х Рисунок 13

Якобиан перехода от декартовых координат к цилиндрическим координатам .

Для вычисления объема тела в цилиндрической системе координат справедлива следующая формула:

или

.

В нашем случае (см. рис. 12) а находим из уравнения параболоида, учитывая цилиндрические координаты:

и, таким образом, .

С учетом вышесказанного имеем:

Ответ: ед³.

16. б) Найти объем тела, ограниченного сферой и конусом , через тройной интеграл, применяя сферическую систему координат.

Решение. Сделаем чертеж, учитывая, что центр сферы находится в начале координат (0; 0; 0), радиус равен 3; осью вращения конуса является ось Оz, а угол между осью Оz и образующей конуса равен (так как каноническое уравнение конуса вращения , где – угол между образующей конуса и осью вращенияОz).

z

3

–3 3 у

3

х

Рисунок 14

С учетом характера области интегрирования вычисления удобно вести в цилиндрических координатах.

Зависимость между декартовыми и цилиндрическими координатами точки имеет вид:

где угол равен углу между осьюОх (х>0) и , уголравен углу между осьюОz (z>0) и ,и .

z qМ(j;q;r) r 0 у j М¢ х Рисунок 15

Якобиан перехода от декартовых координат к цилиндрическим координатам .

Для вычисления объема тела в сферической системе координат справедлива следующая формула:

.

В нашем случае (см. рис. 14) и

Ответ: ед³.

17. а) С помощью двойного интеграла вычислить координаты центра тяжести фигуры (меньшей по площади), ограниченной эллипсом и прямой (поверхностную плотность считать равной единице).

Решение. В случае однородной пластины, занимающей область плоскостихОу, координаты центра тяжести находят по формулам:

где – площадь области,

.

В рассматриваемом случае фигура ограничена кривыми ипри.

у

3

–5 0 5 х

–3

Рисунок 16

Поэтому

Полученный интеграл вычислим заменой переменной.

Итак, . Далее

Первый из полученных интегралов вычисляется с помощью замены переменной:

Отсюда

.

Наконец,

17. б) С помощью двойного интеграла вычислить координаты центра тяжести фигуры, ограниченной линиями (поверхностную плотность считать равной единице).

Решение.

у

3

–9 3 х

3

Рисунок 17

Поскольку фигура симметрична относительно оси Ох, то . Вычислим.

Таким образом, .

18. Вычислить работу, совершаемую переменной силой по контуру, связывающему точкиМ(1; 1) и N(2; 3), и установить независимость от пути интегрирования.

Решение. Для того, чтобы найти работу, совершаемую переменной силой , вычислим криволинейный интеграл

по контуру, соединяющему точки М(1; 1) и N(2; 3).

Выберем в качестве контура интегрирования наиболее простой контур, связывающий точки М и N, например, ломаную, звенья которой параллельны осям координат.

у

3 N

х= 2

у= 1

1 М

0 1 2 х

Рисунок 18

Имеем на первом участке , на втором участке. Таким образом,

В данном случае выполнено условие независимости криволинейного интеграла от пути интегрирования

,

где ,. Действительно,.

19. Найти циркуляцию векторного поля вдоль линии пересеченияплоскостис координатными плоскостями непосредственно и по формуле Стокса (точка пробегает полученную линию против часовой стрелки, если смотреть от начала координат).

Решение. 1) Вычислим циркуляцию по контурунепосредственно по формуле

z

С3 3А

В

0 6 у

х

Рисунок 19

В нашем случае и уравнениеАВ: ,, откудаи, причем. Поэтому

ВС: ,,и, и.

СА: .

.

Окончательно Ц .

2) Вычислим циркуляцию по формуле Стокса.

, где

.

Предварительно найдем ротор вектора :

За поверхность, натянутую на контур, берем поверхность . Тогда

(– площадь,– площадь ).

20. Дано векторное поле и точки ,и.

1) Показать, что поле – потенциальное.

2) Найти потенциал , если известно, что.

3) Найти работу поля между точками и,и,ии найти циркуляцию по контуру.

Решение. 1) Одним из признаков потенциального поля является равенство нулю ротора вектора поля.

.

В нашем примере и

таким образом, и заданное векторное поле является потенциальным.

2) Для потенциального поля вектор поля , где– потенциал поля, то есть

.

Потенциал поля находим по формуле

.

.

Проверка: .

Из условия находимС:

и потенциал поля равен

.

3) Работа потенциального поля между точками иравна разности значений потенциала в конечной и начальной точках.

Циркуляция потенциального поля по замкнутому контуру

.

Проверили еще один признак потенциального поля: циркуляция потенциального поля вдоль любого замкнутого контура равна нулю.

Ответ: 1. ,

2. ,

3. .

21. Найти вероятность безотказной работы участка цепи, если известно, что каждый -ый элемент работает независимо от других с вероятностью(= 1, 2, 3, 4, 5, 6).

.

Рисунок 20

Решение. Участок цепи будет работать безотказно, если работают блоки 1–2 и 3–4–5–6 (последовательное соединение).

Рассмотрим блок 1–2. Элементы 1 и 2 соединены параллельно, следовательно, блок 1–2 будет работать, если хотя бы один из элементов 1, 2 исправен.

–надежность блока 1–2.

Рассмотрим блок 3–4–5–6. Блок 3–4–5–6 будет безотказно работать хотя бы в одном из случаев:

исправны элементы 3 и 4,

исправен элемент 5,

исправен элемент 6.

–вероятность безотказной работы блока

3–4.

–надежность блока 3–4–5–6.

Следовательно,

–искомая надежность участка

цепи.

22. Рабочий обслуживает четыре однотипных станка. Вероятность того, что любой станок в течение часа потребует внимания рабочего, равна 0,6. Предполагая, что неполадки на станке независимы, найти вероятность того, что в течение часа потребуют внимания рабочего: 1) все четыре станка; 2) ни один станок; 3) по крайней мере один станок.

Решение. Обозначим через события, состоящие в том, что в течение часа потребуют внимания рабочего соответственно первый, второй, третий, четвертый станки. По теореме умножения вероятностей независимых событий вероятность того, что в течение часа все станки потребуют внимания рабочего, то есть произойдут события и, и, и, и, вычислим по формуле

.

Вероятность того, что в течение часа станок (любой) не потребует внимания рабочего, найдем по правилу вычисления вероятности противоположного события:

.

Следовательно, вероятность события В, состоящего в том, что ни один станок в течение часа не потребует внимания рабочего, то есть произойдут события и , и, и, и, равна

.

Событие, состоящее в том, что в течение часа по крайней мере один из четырех станков потребует внимания рабочего, и событие В являются противоположными. Поскольку , то

.

23. Заданы законы распределения двух независимых случайных величин Х и У

	Х	–5	2	3	4		У	1	4
	Р	0,4	0,3	0,1	0,2		Р	0,2	0,8

Найти математическое ожидание и дисперсию для случайной величины

.

Решение. Найдем математические ожидания и дисперсии случайных величин Х и У:

Напишем законы распределения для случайных величин и:

	Х ^2	25	4	9	16		У ^2	1	16
	Р	0,4	0,3	0,1	0,2		Р	0,2	0,8

Найдем математические ожидания для случайных величин и:

Отсюда

Пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин Х и У, получаем

24. Станок-автомат изготавливает шарики. Шарик считается годным, если отклонение Х его диаметра от проектного размера по абсолютной величине меньше 0,9 мм. Считая, что случайная величина Х распределена нормально с нулевым математическим ожиданием и со средним квадратическим отклонением мм, найти, сколько процентов годных шариков изготовляет станок-автомат.

Решение. Воспользуемся формулой для вычисления вероятности заданного отклонения нормально распределенной случайной величины Х от ее математического ожидания

,

где – функция Лапласа (см. таблицу значений функции Лапласа).

По условию , поэтому

.

Таким образом, станок-автомат изготовляет 92,8% годных шариков.

25. Измерены диаметры для 60 деталей, обрабатываемых на некотором станке. Данные замеров приведены в табл. 3.

Таблица 3

70,88	67,04	69,20	66,24	64,80	71,52	67,52	68,96	67,36	68,64
67,12	66,96	69,04	66,00	66,00	64,88	65,84	67,52	65,68	70,00
70,80	66,32	67,40	66,08	69,76	68,01	65,76	69,20	65,60	66,72
67,44	67,72	68,72	64,00	66,32	68,21	70,96	67,76	66,88	69,12
65,84	64,88	69,46	68,48	65,04	70,00	70,16	68,72	67,04	69,36
66,48	68,20	64,72	70,40	67,76	69,28	71,20	67,90	66,80	70,24

Выполнить статистическую обработку результатов измерений по следующему плану:

1. Построить статистическое распределение выборки.

2. Выполнить точечные оценки среднего значения и дисперсиислучайной величины.

3. Построить гистограмму относительных частот, установив статистический (эмпирический закон распределения).

4. На том же чертеже построить кривую нормального распределения с параметрами ии проанализировать, хорошо ли статистические данные описываются нормальным законом распределения.