
- •Оглавление
- •Источники погрешностей при вычислениях по формулам.
- •1.1.Абсолютная и относительная погрешности. Оценки погрешностей
- •1.2. Границы значений числовых величин
- •1.3. Запись приближенных значений. Верные знаки
- •1.4. Округление. Погрешность округления. Первое правило подсчета верных знаков
- •Первое правило верных знаков
- •1.5. Линейные оценки погрешностей.
- •Линейные оценки погрешностей для функций нескольких переменных.
- •1.6. Метод границ
- •1.7. Правила подсчета верных знаков.
- •Контрольные вопросы
- •Литература
- •Тема 2. Численные методы решения уравнений с одним неизвестным
- •2.1. Постановка задачи. Метод последовательных приближений. Отделение корней
- •Отделение корней
- •Общая характеристика итерационных методов решения уравнений.
- •2.2. Метод половинного деления
- •2.3. Метод простой итерации
- •2.4. Метод касательных
- •2.5. Метод секущих
- •Оценка погрешности методов.
- •2.6. Комбинированный метод секущих и касательных
- •Контрольные вопросы
- •Литература
- •Тема 3. Численные методы решения систем уравнений
- •3.1. Постановка задачи
- •Общая характеристика численных методов решения систем линейных уравнений
- •3.2. Метод Гаусса
- •3.3. Метод простой итерации решения систем линейных уравнений
- •Контрольные вопросы
- •Литература
- •Тема 4. Интерполирование функций
- •4.1. Постановка задачи
- •4.2. Интерполяционный многочлен Лагранжа
- •Оценка погрешности интерполяционных формул
- •Контрольные вопросы
- •Литература
- •Тема 5. Наилучшее среднеквадратическое приближение
- •5.1. Аппроксимация функций методом наименьших квадратов
- •Нахождение приближающей функции в виде квадратного трехчлена
- •Контрольные вопросы
- •Литература
- •Тема 6. Численное интегрирование
- •6.1. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона–Котеса
- •Формулы прямоугольников
- •Формула трапеций
- •Формула Симпсона (парабол)
- •6.2. Принцип Рунге оценки погрешностей
- •6.3. Статистический метод вычисления интегралов
- •I схема метода Монте–Карло
- •II схема метода Монте - Карло
- •Нахождение первообразной
- •Контрольные вопросы
- •Литература
- •Глоссарий
Контрольные вопросы
Запишите алгоритм метода Гаусса с выбором главных элементов в столбцах для решения линейной системы.
Как конкретизируется принцип сжимающих отображений для приближенного решения линейных систем?
Запишите алгоритм метода простой итерации для решения линейной системы.
Запишите и обоснуйте условия при которых отображение F является сжимающим.
Как приводится линейная система к виду, удобному для применения метода простой итерации?
Литература
Вержбицкий В.М. Основы численных методов. М.: Высшая школа, 2002.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. -М., Наука, 1987.
Вабищевич П.Н.. Численное моделирование. М.: 1993.
Заварыкин В. М., Житомирский Г. В., Лапчик М. П. Численные методы. - М., Просвещение, 1990.
Тема 4. Интерполирование функций
Цель: Сформировать у студентов представление об интерполировании функций.
Вопросы:
Постановка задачи.
Интерполяционный многочлен Лагранжа.
4.1. Постановка задачи
Пусть известные значения некоторой функции f образуют таблицу:
-
x



…

f(x)


…

При этом требуется
получить значение функции f
для такого значения аргумента x,
которое входит в отрезок [![]() ],но
не совпадает ни с одним из значений
(i=0,1,…,n).
Поскольку чаще всего аналитическое
выражение функции f
неизвестно, то используют следующий
прием: подбирают функцию g(x),
приближающую функцию f(x)
в промежутке [
],но
не совпадает ни с одним из значений
(i=0,1,…,n).
Поскольку чаще всего аналитическое
выражение функции f
неизвестно, то используют следующий
прием: подбирают функцию g(x),
приближающую функцию f(x)
в промежутке [![]() ].
].
Классический
подход к решению задачи построения
приближающей функции основывается на
требовании строго совпадения значений
f(x)
и g(x)
в точках
![]() (i=0,1,…,n),
то есть
(i=0,1,…,n),
то есть
![]()
В этом случае нахождение приближающей функции называют интерполяцией (или интерполированием), а точки – узлами интерполяции.
Очевидно, что задача интерполяции допускает сколь угодно много решений. Обычно, функцию g(x) выбирают из функций определенного класса и чаще всего из класса многочленов.
Будем искать
интерполирующую функцию g(x)
в виде многочлена степени ≤ n:
![]() причем
причем
![]() ,
,
![]() .
Многочлен
.
Многочлен
![]() называютинтерполяционным
многочленом
для функции f(x),
построенным по узлам
называютинтерполяционным
многочленом
для функции f(x),
построенным по узлам
![]() .
.
Для любой функции f(x) сформулированная задача имеет решение, причем единственное. Для того чтобы это показать, поступим следующим образом. Для определения коэффициентов многочлена составим систему уравнений, которая имеет следующий вид:

Получим систему из (n+1)–го линейного уравнения с (n+1)–им неизвестным. Найдем определитель этой системы:

Если все точки
![]() различны, то этот определитель отличен
от 0. Следовательно, рассматриваемая
система уравнений всегда имеет решение,
причем единственное.
различны, то этот определитель отличен
от 0. Следовательно, рассматриваемая
система уравнений всегда имеет решение,
причем единственное.
Описанный прием в принципе можно было бы использовать и для практического решения задачи интерполированием многочленом, однако на практике используют другие, более удобные и менее трудоемкие способы.
4.2. Интерполяционный многочлен Лагранжа
Рассмотрим следующий многочлен:
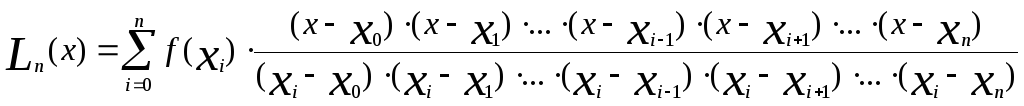 (1)
(1)
или кратко

Не трудно проверить,
что степень этого многочлена ≤ n
. Покажем, что значения этого многочлена
в точках
![]() совпадают
со значением функцииf(x),
то есть
совпадают
со значением функцииf(x),
то есть
![]() .
Чтобы это показать, рассмотрим следующий
многочлен:
.
Чтобы это показать, рассмотрим следующий
многочлен:
![]()

Найдем его значения
в узлах интерполяции:

Заметим, что
![]() можно
переписать в следующем виде:
можно
переписать в следующем виде:
![]() Рассмотрим
Рассмотрим
![]() в точке
в точке
![]() :
:
![]() =
=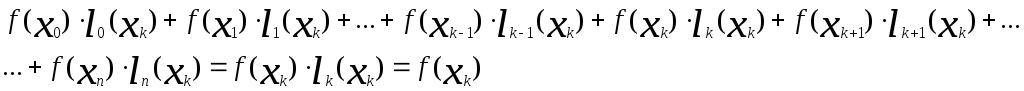
Итак, мы доказали,
что многочлен
![]() имеет степень не вышеn
и в узлах интерполяции его значения
совпадают с соответствующими значениями
функции f(x).
А в силу того, что интерполяционный
многочлен единственен, то
имеет степень не вышеn
и в узлах интерполяции его значения
совпадают с соответствующими значениями
функции f(x).
А в силу того, что интерполяционный
многочлен единственен, то
![]() одно из представлений этого многочлена.
одно из представлений этого многочлена.
Интерполяционный
многочлен в форме (1) называют
интерполяционным
многочленом Лагранжа,
а формула f(x)![]()
![]() называетсяинтерполяционной
формулой Лагранжа.
называетсяинтерполяционной
формулой Лагранжа.
