Нахождение приближающей функции в виде квадратного трехчлена

F(x, a, b, c)=a+bx+c. Находим частные производные: ,Составляем систему:

где . Решение системы даст значение коэффициентов a, b, c и конкретный вид квадратичной функции.

Нахождение приближающей функции в других семействах

При поиске решений в других семействах функций с двумя параметрами используют формулы линейной аппроксимации, предварительно делая замену переменных.

1. y=aU=, V=yV= aU+b

2. y=при xV=U=A=b, B=aV=AU+B

3. y=ax^b прологарифмируем lny=lna+blnx U=lnx, V=lny, A=b, B=lna V=AU+B

4. y=ae^bx lny=lna+bx U=x, V=lny, A=b, B=lna V=AU+B

5. y=U=x, V=V=aU+b

6. y=alnx+b U=lnx, V=y V=aU+b.

При этом решении задачи складывается из следующих этапов:

1. Определить по расположению табличных точек на графике семейство, в котором нужно искать приближение.

2. Применить соответствующую формулу замены переменных, перевести это семейство в линейное.

3. Найти новую таблицу значений линейной функции (по формулам замены).

4. На основе новой таблицы найти коэффициенты линейной функции методом наименьших квадратов.

5. По найденным коэффициентам линейной функции найти коэффициенты искомой функции выбранного семейства.

Контрольные вопросы

1. Опишите общую схему метода наименьших квадратов.

2. Как строятся полиномиальная и линейная аппроксимация по методу наименьших квадратов?

3. Как производится поиск наилучших приближений по методу наименьших квадратов в некоторых двухпараметрических семействах нелинейных функций: , ,, , ,.

Литература

1. Вержбицкий В.М. Основы численных методов. М.: Высшая школа, 2002.

2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. -М., Наука, 1987.

3. Вабищевич П.Н.. Численное моделирование. М.: 1993.

4. Заварыкин В. М., Житомирский Г. В., Лапчик М. П. Численные методы. - М., Просвещение, 1990.

Тема 6. Численное интегрирование

Цель: Сформировать у студентов представление о методах численного интегрирования.

Вопросы:

6.1. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона–Котеса.

6.2. Принцип Рунге оценки погрешностей.

632. Метод статистических испытаний.

6.1. Постановка задачи численного интегрирования. Квадратурные формулы Ньютона–Котеса

При вычислении определенных интегралов по формуле Ньютона-Лейбница возникают определенные сложности:

1. даже в простейших случаях точное вычисление первообразной требует больших выкладок.

2. Даже для элементарной функции числа не выражаются через элементарную функцию (а только суммой ряда)

3. При известном аналитическом виде первообразной возникают проблемы вычисления точного её значения.

Т.о. для решения целого ряда прикладных задач необходима метода, позволяющая быстро и с любой точностью находить значения интегралов.

Существует два основных подхода:

1. применение т.н. квадратурных формул

2. статистические методы.

Для получения квадратурной формулы обычно используется интерполяция, например многочлен Лагранжа.

Так как , где узлы интерполяции,

(2)

где зависят только от выбора и расположения точек,.

Формулы прямоугольников

Формула прямоугольников получается из (2) если положить в зависимости от расположения точки. При этом, для повышения точности вычисления, отрезок интеграла разбивают на части таким образомБудем выбирать 1)2)3)

Таким образом, если {x_i} – разбиение отрезканаk равных частей с шагом , шаг квадратурной формулы, таким образом:

формула правых прямоугольников

формула левых прямоугольников

(*)формула средних прямоугольников

последняя формула в силу очевидных геометрических соображений является более точной, её будем называть формулой прямоугольников

Однако произвести оценку погрешности невозможно без дополнительных предположений относительно гладкости функции .

Пусть

Вычислим сначала ; гдеh<<1.

формула Тейлора. 2^го порядка и

/

таким образом, приблизительное значение по формуле прямоугольников,

В общем случае где,
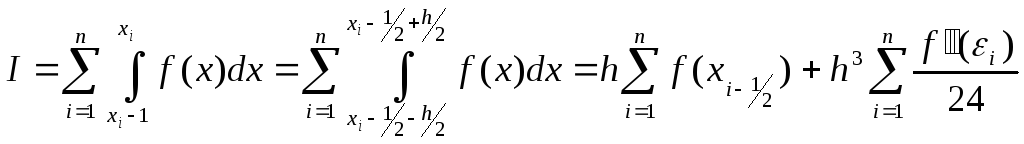