Формула трапеций

Пусть разбиение. Запишем на каждом частичном отрезкемногочлен Лагранжа

,

Тогда

Положим

Для оценки погрешности необходимо интегрировать остаточный член функции интерполяции

Т.о.

Формула Симпсона (парабол)

Используем теперь интегральную формулу приn=2, т.е. на каждом частичном отрезке запишем функцию параболы.

Рассмотрим частичный отрезок, положим для удобства

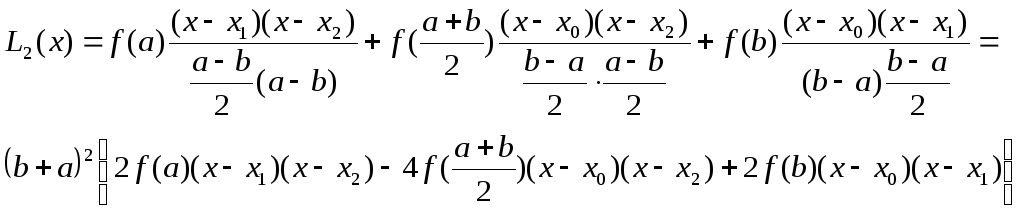
Т.о.

Интегрируя остаток интерполяционной формулы, получим формулу оценки погрешности:

6.2. Принцип Рунге оценки погрешностей

Недостатком рассмотренных ранее методов численного интегрирования является необходимость заранее определять шаг интегрирования вручную. (исходя из max производных) Пусть интеграл I вычислен по одной из квадратурных формул

Если функция достаточно гладкая f(x)C^p[a;b], то :

(1) (h – шаг интегрирования)

С уменьшением шага (2)

Причем при малых h можно считать что

Т.о.

Т.о. эта формула даёт возможность контролировать (грубо) погрешность приближения в зависимости от шага интегрирования.

Полученная формула позволяет провести вычисление следующим образом:

1. Полагают ;

2. Вычисляют

3. и вычисляют ;

4. Оценивают погрешность

5. Если 

Если полагают и повторяют вычисления с шага 3.

Этот алгоритм носит название правила Рунге или метода повторного счета.

6.3. Статистический метод вычисления интегралов

Метод вычисления, основанный на статистических методах, чаще всего применяют для вычисления кратных интегралов (n≥ 4). Мы рассмотрим эти методы на примере определенного интеграла.

I схема метода Монте–Карло

С помощью генератора случайных чисел можно получить последовательность равномерно распределенных значений α_i некоторой случайной величины α, которые характеризуются тем, что вероятность появления значения из интервала не зависит от положения этого интервала и .

Как известно

Можно приближенно заменить функцию f(x) набором равномерно распределенных значений и заменитьт.е. средним арифметическим дискретных значений функции.

Т.о. учитывая что (доказывается в теории вероятности), то

Пусть задан иj_i =random случайная величина из

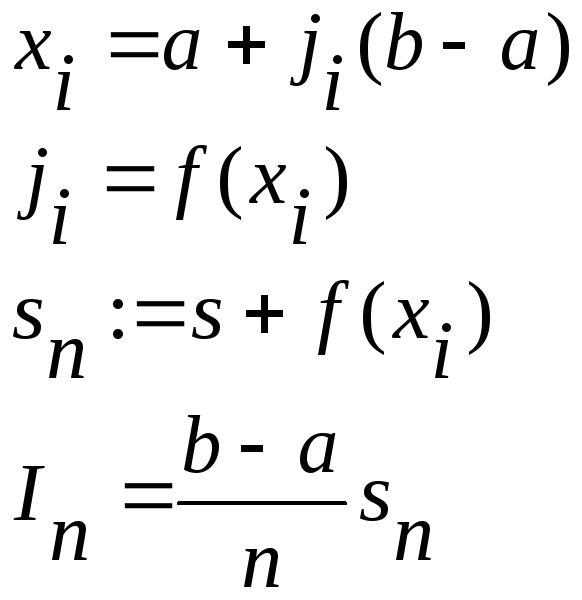
Оценки для определения погрешности этой функции не существует. Скорость приближения I_n→ I определяется экспериментально. Задается цикл порядка n≥10⁴.И в процессе вычисления интеграла выводятся все значения I_I. При стабилизации значащих цифр в соответствующем разряде считается, что требуемая точность достигнута.

Формулу I метода Монте-Карло в изначальном виде интерполировать неудобно из-за повторяющего вычисления суммы одних и тех же значений

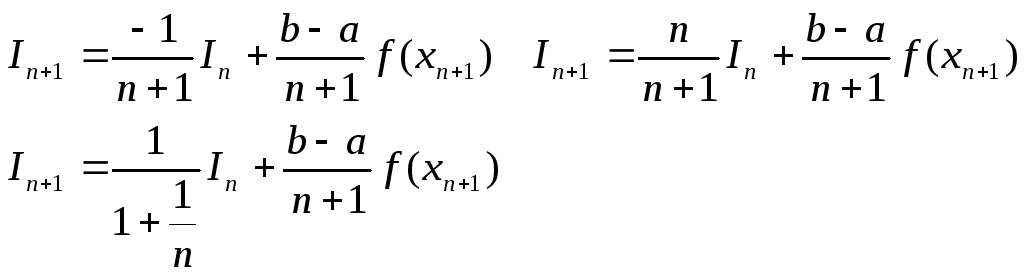
В этой рекуррентной формуле полагают I_I=(b-a)f(x₁) ()

II схема метода Монте - Карло

Основана на геометрическом подходе. Содной стороны

S – площадь криволинейной трапеции

S₀

f

S

a b

С точки зрения теории вероятности доказывается, что, гдеS₀ – площадь прямоугольника, содержащего S, а Р – вероятность попадания точки, выбранной случайно из S₀ в S.

Пусть _i., J_i =random [0, 1], тогда ,. Криволинейная трапеция определяется условиямиa≤x≤b, 0≤y≤f(x). Т.е. если точка с координатами (x_i,y_i) принадлежит прямоугольнику S₀ и j_i≤f(x_i), то она принадлежит и трапеции S.

Пусть n – общее количество итераций N(n) – число точек, принадлежащих трапеции, тогда (закон больших чисел)

Т.о. , последовательность

Оценка погрешности, как и в первом случае, проводится на основе экспериментальных данных стабилизации разрядов в приближенном значении.

Очевидно, если функция (x) меняет знак на или является неположительной, можно рассмотреть функциюгде