§4. Вычисление двойного интеграла повторным интегрированием
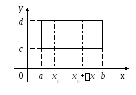
I случай. Прямоугольная область.
Пусть функция
f(x;y)
определена на прямоугольнике
Р=[a,b;c,d]
и интегрируема по y
на [c;d]
для любого фиксированного x[a;b],
т.е. x[a;b]
.
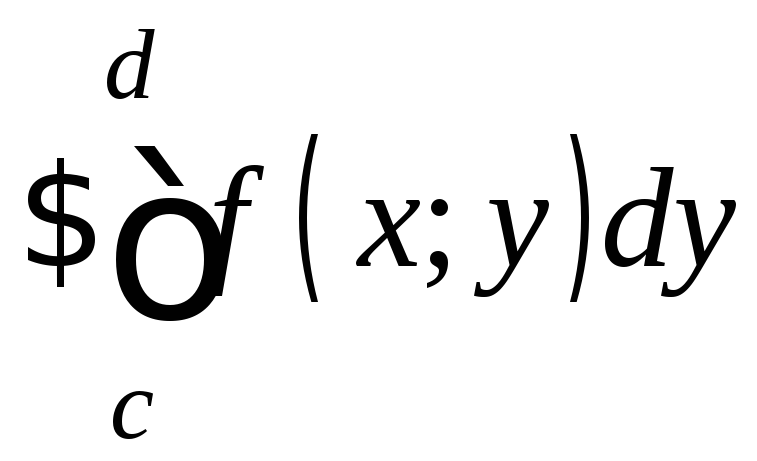Тем самым определена функция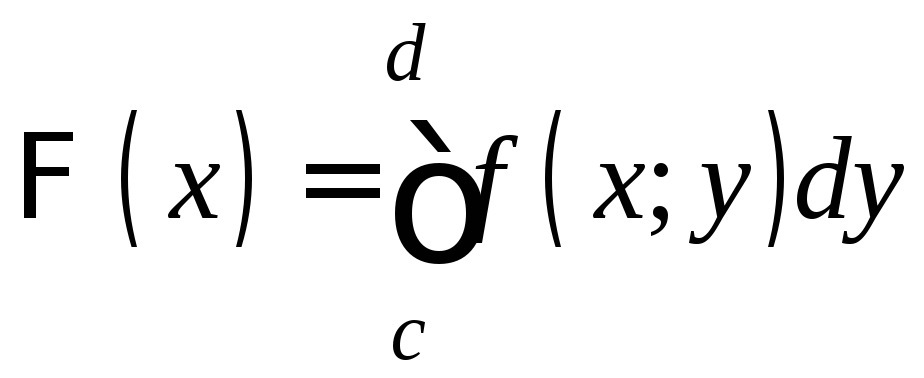
на [a;b].
Если функция (х)
интегрируема на [a;b],
т.е.
,
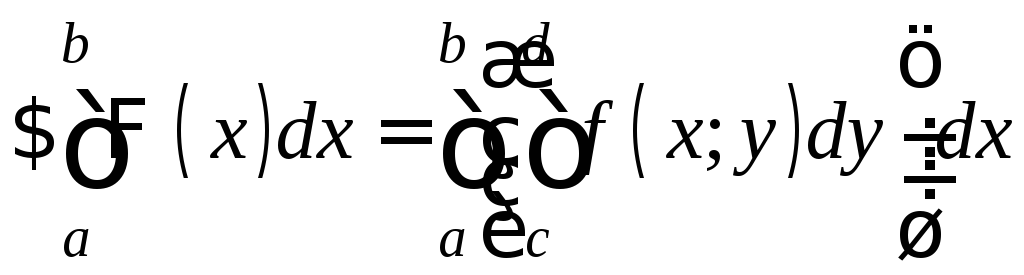тоэтот
интеграл называется повторным
интегралом от
функции f
по прямоугольнику Р,
взятым сначала по y,
а затем по x.
Его символически обозначают
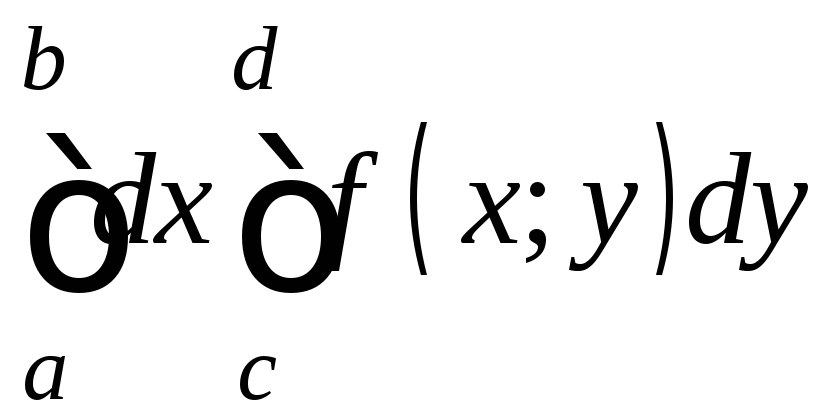. (1)
Аналогично
определяется повторный интеграл
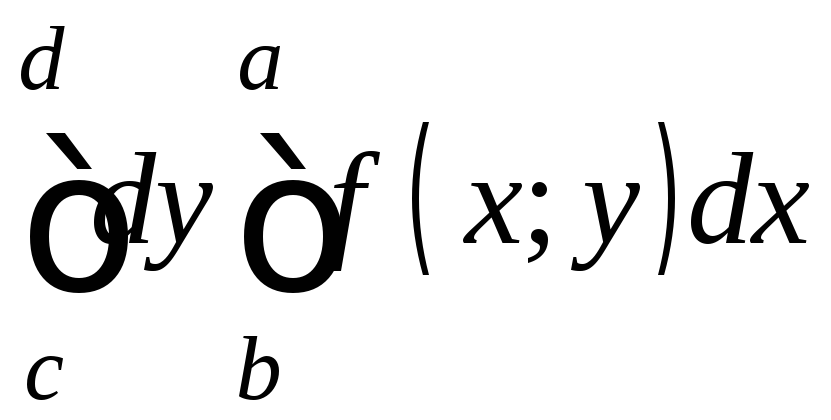. (2)
Теорема
1.
Если функция
f(x;y)
непрерывна на прямоугольнике Р=[a,b;c,d],
то существуют повторные интегралы (1) и
(2).
Доказательство.
Докажем существование
интеграла (1). Для этого достаточно
доказать, что функция
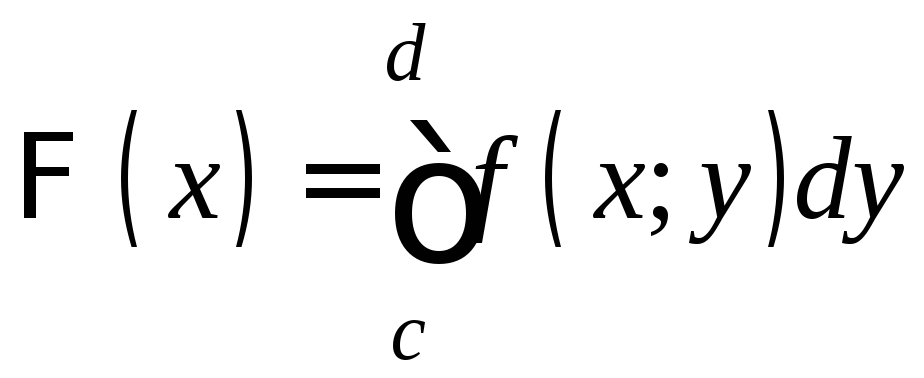непрерывна на [a;b].
Пусть x0
- произвольная точка отрезка [a;b].
Придадим x0
приращение х,
так чтобы x0+х[a;b].
Тогда
,
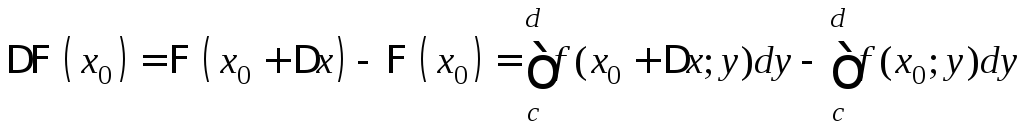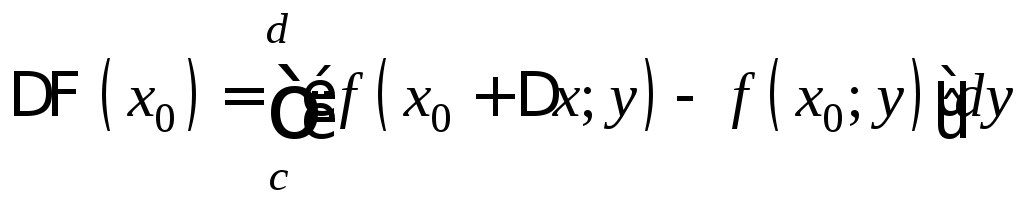. (3)
Т.к. функция f непрерывна на прямоугольнике Р, то она и равномерно непрерывна на нём. Тогда >0 >0: (x1;y1),(x2;y2)P: ((x1;y1),(x2;y2))<
|f(x1;y1)-f(x2;y2)|<. (4)
Пусть >0
- произвольное число.
выполнено
,
.
Тогда для этих точек должно выполняться (4), т.е.
. (5)
Из (3) и(5) следует
.
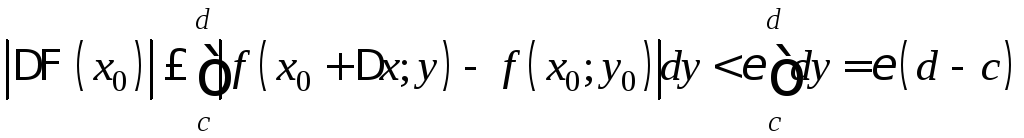Т.о., из условия
следует
.
Следовательно,
(х)
непрерывна в точке х0.
Так как х0
– произвольная точка из [a;b]
то (х)
непрерывна на [a;b].
Следовательно, она интегрируема на
[a;b],
т.е.
.
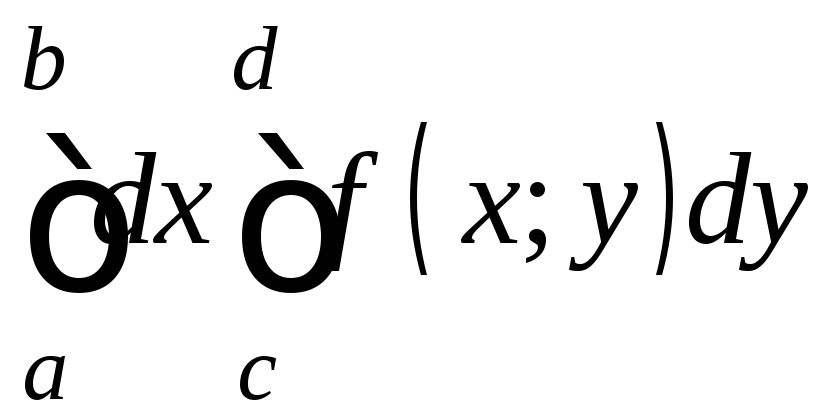Существование
повторного интеграла (2) доказывается
аналогично.
Теорема 2. Если функция f(x;y) непрерывна на прямоугольнике Р=[a,b;c,d], то справедлива формула
.
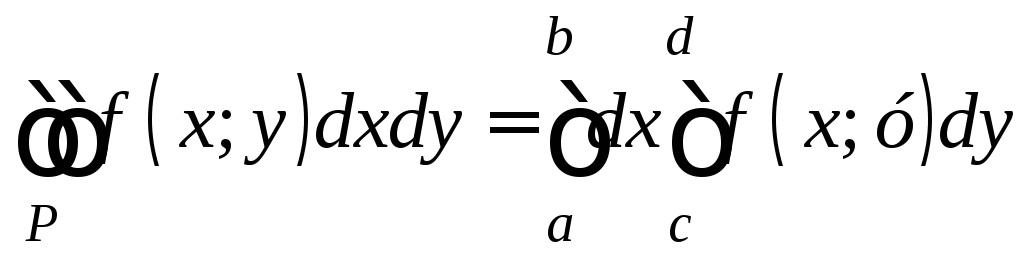
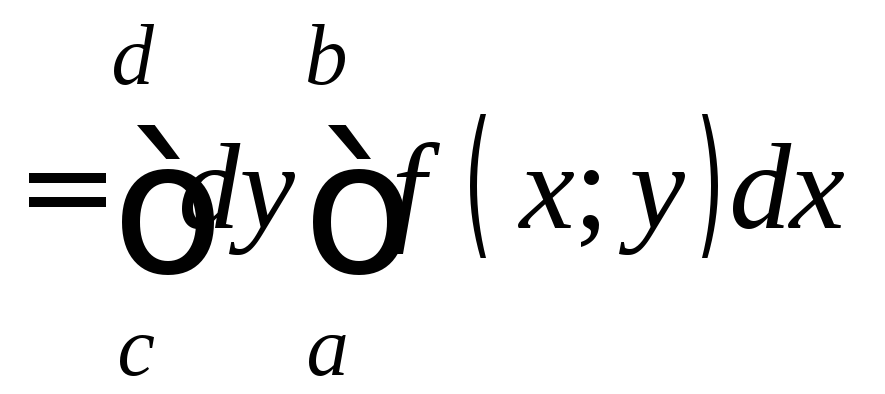(без доказательства)
Пример 1.
Вычислить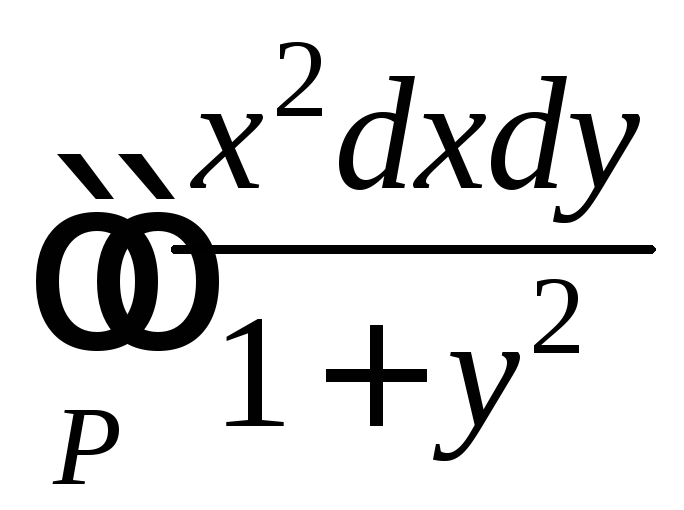 
,
где Р
прямоугольник [0,1;0,1].
.
II случай. Непрямоугольная область.
Пусть
функция f(x;y)
определена на замкнутой области Р,
представляющей собой плоскую фигуру,
ограниченную прямыми x=a
и x=b
(a<b),
кривыми y=1(x)
и y=2(x),
причем 1(x)2(x)
и 1(х),
2(х)
непрерывны на [a;b].
Такую область назовем простой
областью I
типа.
(обозначим её РI).
Очевидно, что
РI
квадрируема. Рассуждая
аналогично I случаю, имеем:
,
повторный интеграл:
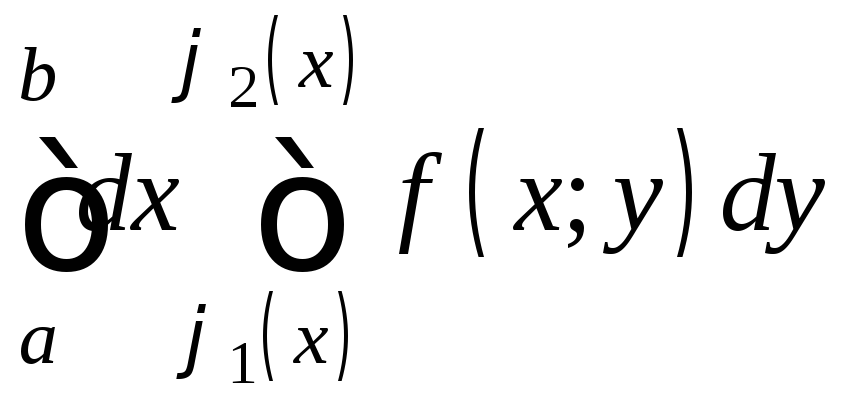. (6)
П
усть
область
Р
ограничена прямыми y=c
и
y=d
(c<d),
кривыми x=1(y),
x=2(y),
причем 1(y)2(y)
и 1(y)
и 2(y)
непрерывны на [c;d].
Такую
область назовем простой
областью II
типа.
(обозначим её РII).
РII
квадрируема. Тогда
,
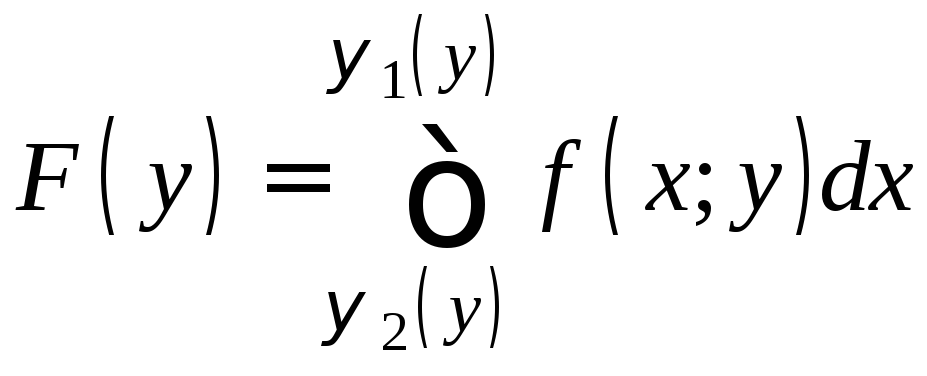повторный интеграл:
.
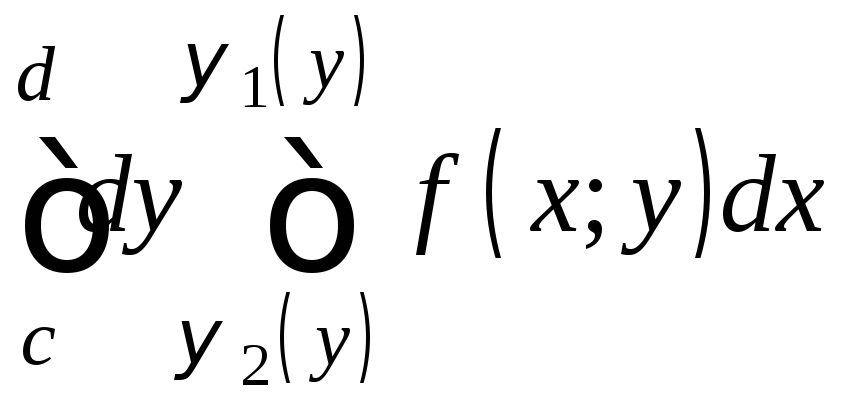(7)
Теорема 3. Если функция f(x;y) непрерывна на простой области I типа, то существует повторный интеграл (6).
Доказательство.
Докажем непрерывность
функции (х)на[a;b].
Из этого будет следовать ее интегрируемость.
Пусть х-
произвольная точка отрезка [a;b].
В интеграле
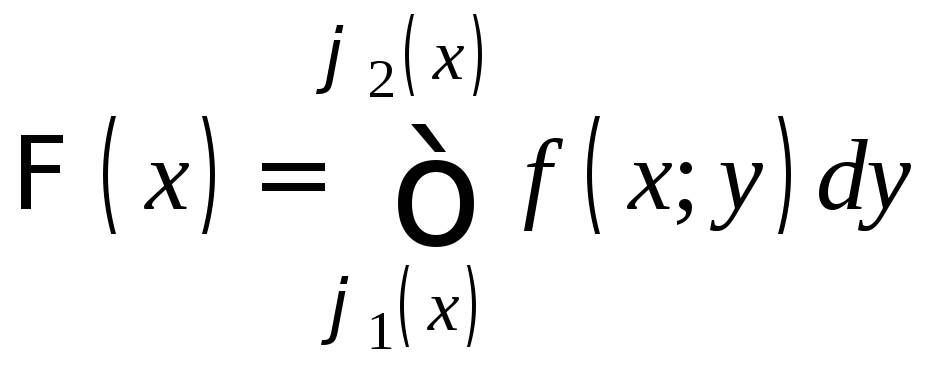сделаем замену переменной:
.
Еслиt=0,
то y=1(x),
если t=1,
то y=2(x),
.
Получим
.
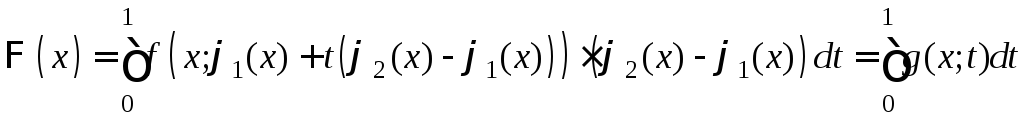Т.к. f(x;y)
непрерывна на РI,
функции 1(х),
2(х)
непрерывны на [a;b],
то функция g(x;t)непрерывна на
прямоугольнике D=[a,b;0,1].
Поэтому на основании теоремы 1 (х)непрерывна на[a;b].
Следовательно, она интегрируема на
[a;b],
т.е.
.
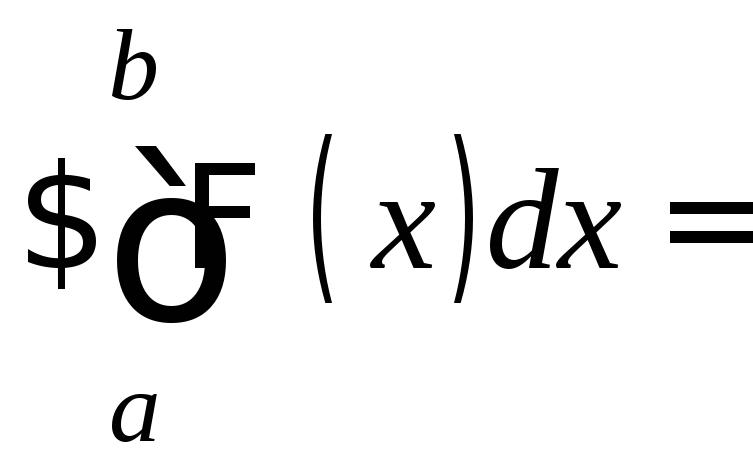
Теорема 4. Если функция f(x;y) непрерывна на простой области II типа, то существует повторный интеграл (7).
Теорема 5. Если функция f(x;y) непрерывна на простой области I типа, то справедлива формула
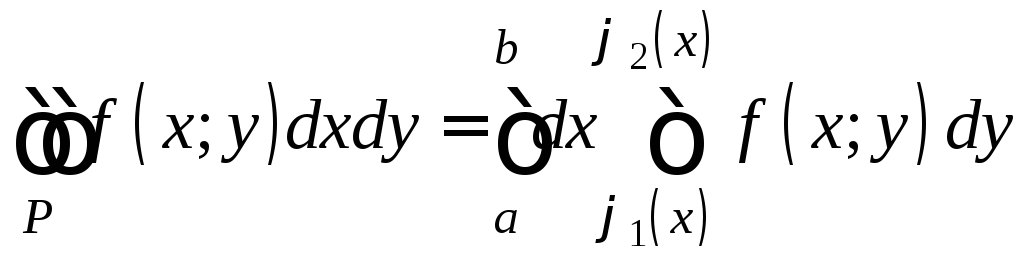. (8)
Доказательство (на оценку «отлично»).
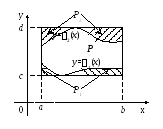Так как 1(x)
и 2(x)
непрерывны на [a;b],
то они на этом отрезке имеют наименьшее
и наибольшее значения. Обозначим их
,
.
Пусть D=[a,b;c,d],
PD.Рассмотрим
функцию F(x;y)
на D:
По условию f непрерывна на замкнутой квадрируемой области Р, следовательно, она интегрируема на Р. Т.к. F(x;y)=f(x;y), то и F(x;y) интегрируема на Р и
.
С другой стороны, т.к. на Р1 и Р2 F(x;y)=0, то F(x;y) интегрируема и на Р1, Р2 и
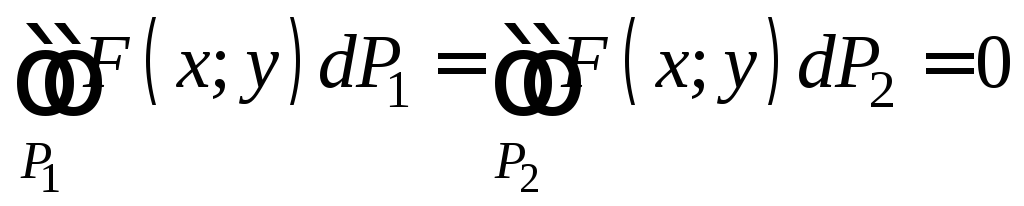
(все интегральные суммы равны нулю, а значения на границе можно не учитывать).
Тогда по свойству аддитивности двойного интеграла F(x;y) интегрируема на
и
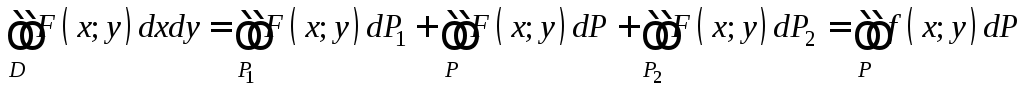. (9)
Теперь наша задача
свелась к вычислению 
- двойного интеграла по прямоугольной
области.
фиксированного х[a;b]
,
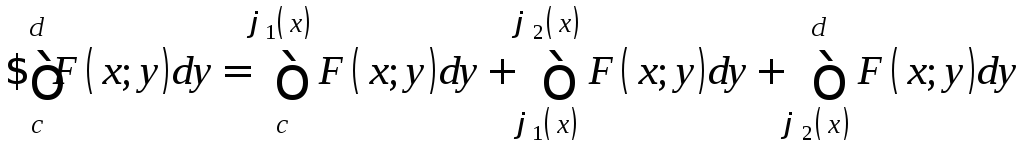так как существует каждый из трёх интегралов справ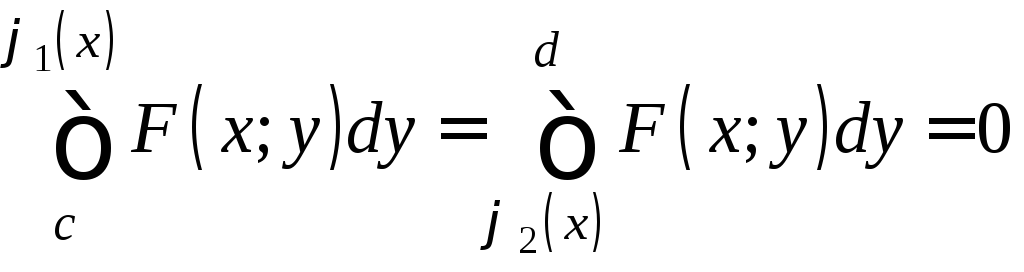а:
,
а
.
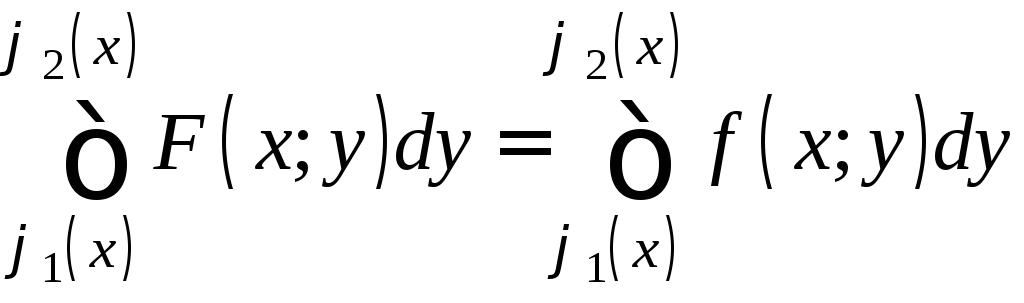Тогда х[a;b]
. (10)
Так как f(x;y)
непрерывна на Р,
то по теореме 3
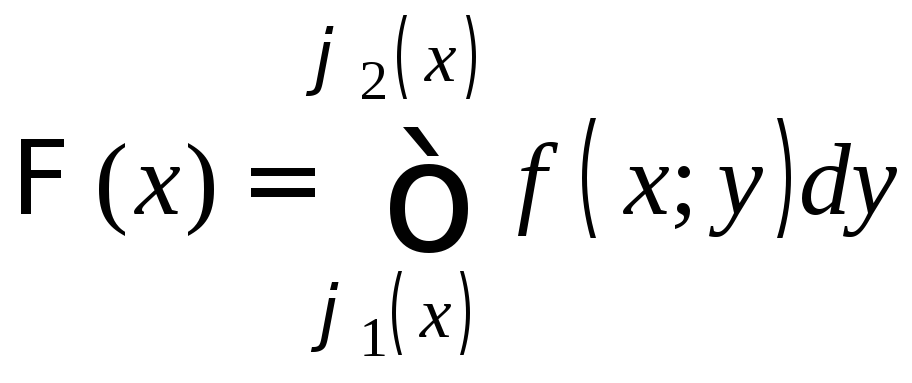непрерывна
на [a;b].
Тогда из (10) следует, что
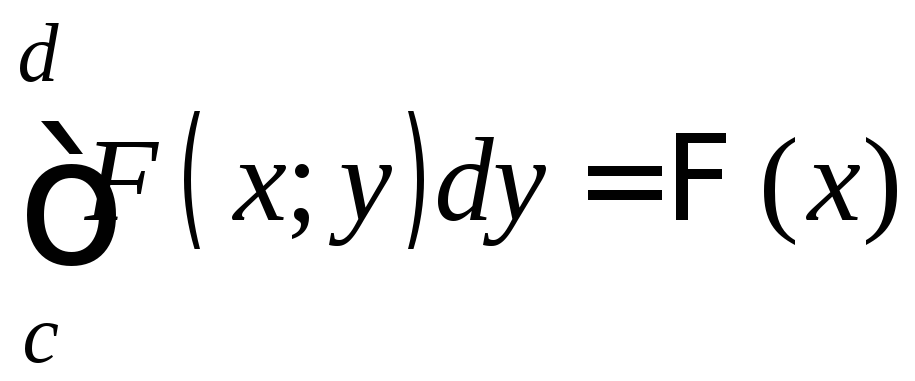непрерывна на [a;b],
значит, (х)
интегрируема на [a;b],
т.е. существует повторный интеграл
(случай I)
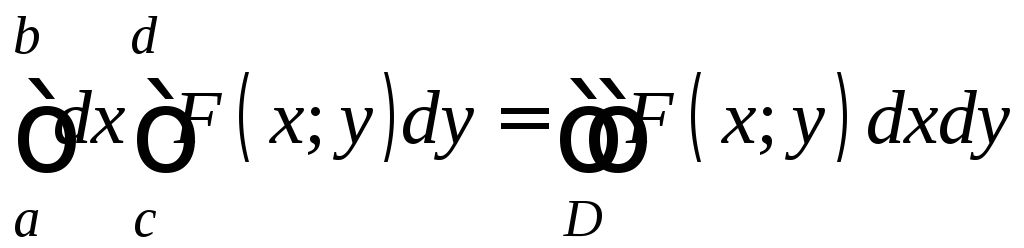. (11)
Теперь из (9) и (11), учитывая (10), получаем
.
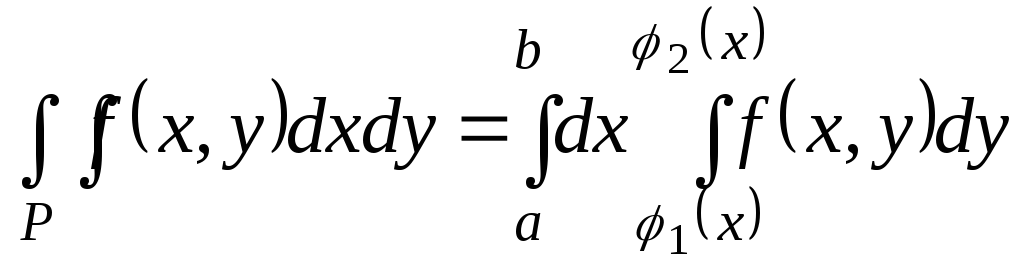Теорема 6. Если функция f(x;y) непрерывна на простой области II типа, то справедлива формула
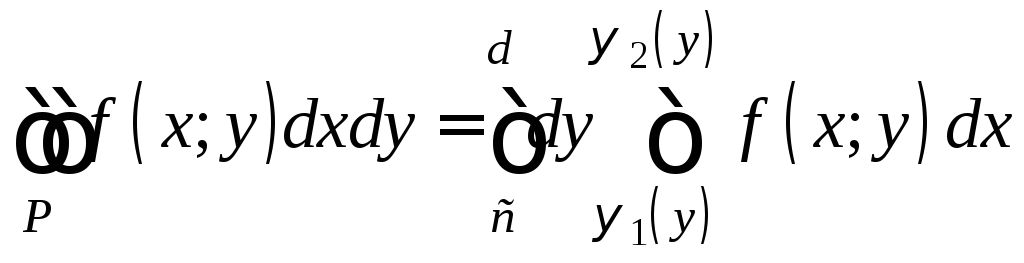. (12)
Замечание
1. Если контур
области интегрирования пересекается
не более, чем в двух точках, как параллелями
оси Ох,
так и параллелями оси Оу,
то имеют место обе формулы (8) и (12), и,
значит, повторные интегралы (6) и (7) равны.
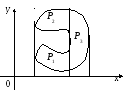
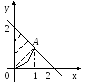Замечание
2. Если область
Р
не является простой областью I или II
типа, то её разбивают (если возможно) на
конечное число простых областей I и II
типа. Тогда двойной интеграл по области
Р
равен сумме интегралов по простым
областям.
Пример 2.
Р
ограничена: y=x3,
y+x=2,
x=0.
Вычислить
.
Найдём координаты точки А:
x3=2-x, x3+x-2=0, x=1.
=
.
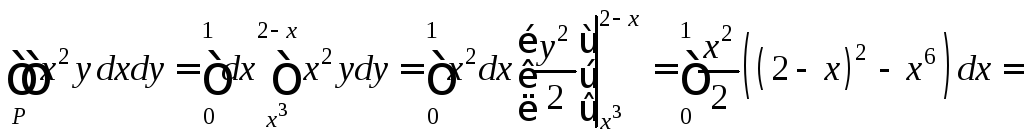
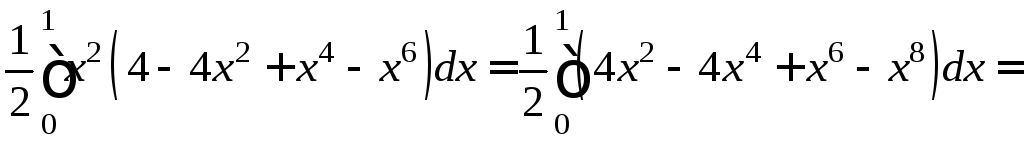
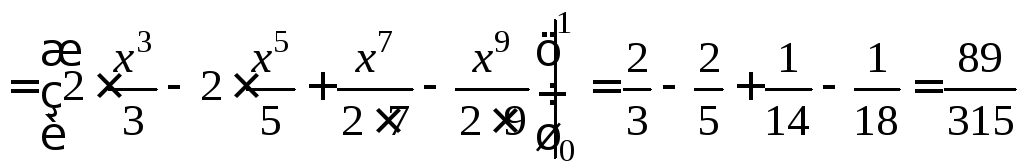П
ример
3. Р
ограничена: y2=3x+9,
y=3–x.
Свести
к повторным двумя способами.
Найдём точки пересечения графиков функций:
(3-x)2=3x+9, 9-6x+x2-3x-9=0,
x2-9x=0, x(x-9)=0, x=0, x=9,
y=3, y=-6.
Выразим из первого уравнения х: 3x+9=y2-9,
.
.
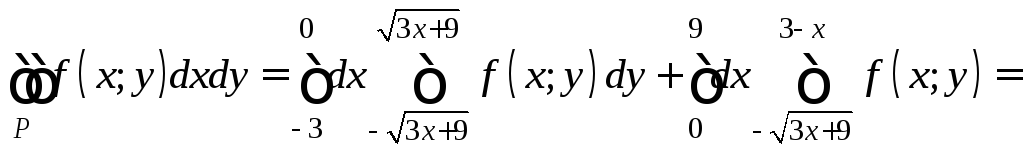
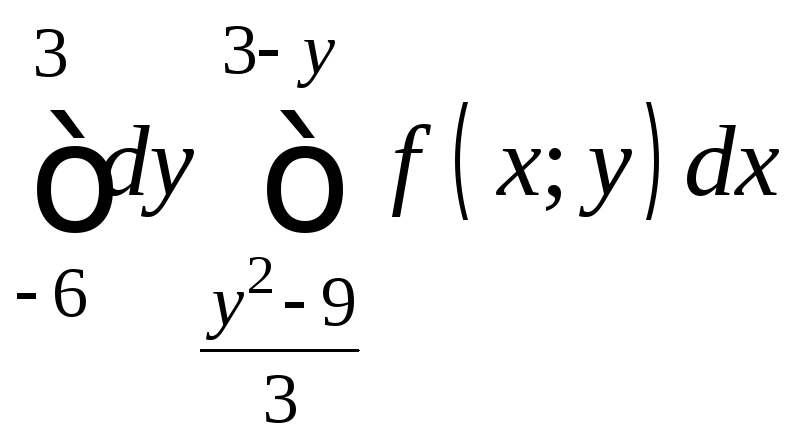