Задание

1. Провести эксперимент с моделью, соответствующей вашему варианту. Модель взять из файла по адресу \\auts0\Student\ИДС\plant_model_2012_5.mdl. Номер модели совпадает с номером вашей бригады. Зафиксировать переходную характеристику.

2. Провести идентификацию с помощью МНК.

3. Верифицировать полученные модели.

5. Сделать выводы о проделанной работе.

Контрольные вопросы

1. Объяснить процедуру параметризации ИПФ.

2. Из каких соображений выбирается длина интервала идентификации ИПФ?

3. Как влияет длина шага симулирования на точность идентификации?

Лабораторная работа №4.

Построение модальных наблюдателей состояния полного порядка

Цель работы.

Смоделировать наблюдатель состояния по желаемым полиномам, соответствующим типовым переходным функциям.

Теоретические сведения.

Часто на практике для измерений доступны не все компоненты вектора состояний. Восстановление вектора состояний называется оценкой. Устройство, формирующее на выходе вектор оценки, а так же позволяющее отделить полезный сигнал от помех, называется наблюдателем.

Асимптотический наблюдатель, который в формирование оценки использует выход системы, доступный для измерений, это асимптотический идентификатор.

12. Рисунок – Асимптотический наблюдатель

В этом случае выход системы сравнивается с выходом идентификатора, и их разность является сигналом ошибки и подается на вход системы в качестве корректирующего воздействия с весовым коэффициентом.

Динамические свойства идентификатора существенно зависят от выбора . За счет выбора этого вектора можно обеспечить желаемый характер стремления разностипри.

Линейная динамическая система, выходом которой является вектор называется асимптотическим идентификатором состояния исходной линейной системы, заданной в пространстве состояний, если разностьпри.

Динамические уравнения асимптотического идентификатора:

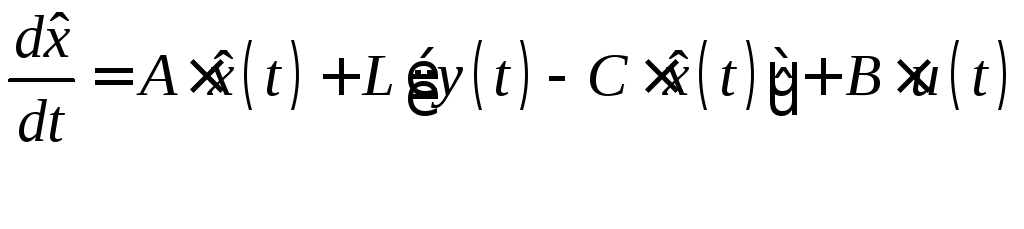
Представим в следующем виде:

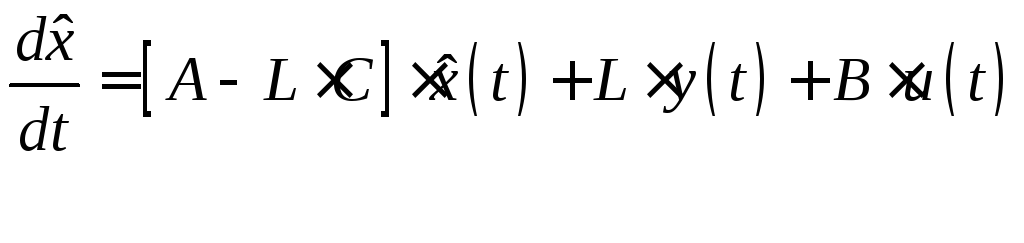
Идея построения асимптотических идентификаторов заключается в следующем, если бы за счет выборов коэффициентов матрицы можно было произвольным образом выбирать характеристический многочлен матрицы, то это бы означало , что можно произвольно менять темп стремления оценкик состоянию.

Например, если все собственные числа матрицы имеют отрицательные действительные части, то все компоненты вектора ошибки приближаются к 0 по экспоненциальному закону.

Желаемая динамика идентификатора может быть выбрана, если система идентифицирована.

Методический пример

Построим следующую схему в Simulink, состоящую из формирующего фильтра и измерителя.

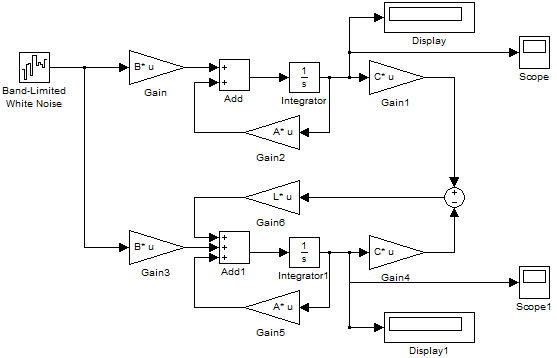
13. Рисунок – Схема

В блоках Gainнеобходимо изменить параметрMultiplicationтак, как показано на рисунке.

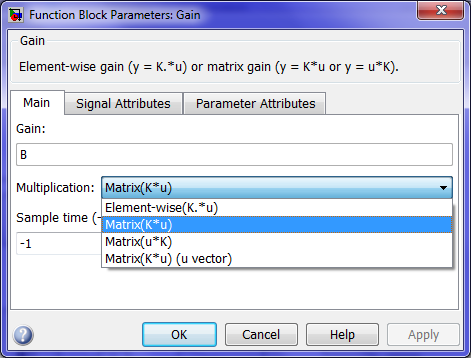
14. Рисунок– Изменение параметра Multiplication

Формирующие фильтры будем брать из таблицы, приведенной ниже.

	a1	a2	a3	w0
Фильтр Баттерворта	2	2	1	1
Фильтр Бесселя	2.4329	2.4662	1	1
Биноминальный полином	3	3	1	1

Построим фильтр Баттерворта.

Матрица коэффициентов усиления фильтра рассчитывается, как:

Реализуем это в Matlab:

i1=tf(13, [10 8 1]);

i2=tf(1, [1 1]);

i3=series(i1,i2);

i4=ss(i3);

[A B C D]=ssdata(i4);

%находим матрицу наблюдаемости

Qn=obsv(A,C);

%найдем корни характеристического уравнения

H=poly(A);

H1=roots(H);

Ki=[2-H1(1) 2-H1(2) 1-H1(3)]';

% найдем нормирующую матрицу

Tn=Qn*1;

Tn1=inv(Tn);

% найдем матрицу коэффициентов усиления фильтра

L=Tn1*Ki

An=A-L*C

В результате получилось:

L =

1.7770

4.0692

1.1538

An =

-1.8000 -0.9000 -5.0202

1.0000 0 -10.5798

0 0.2500 -3.0000

Далее необходимо задать разные начальные условия для интеграторов объекта и формирующего фильтра (1 и 0.1), для этого зададим необходимые значения в параметре InitialconditionблокаIntegrator1.

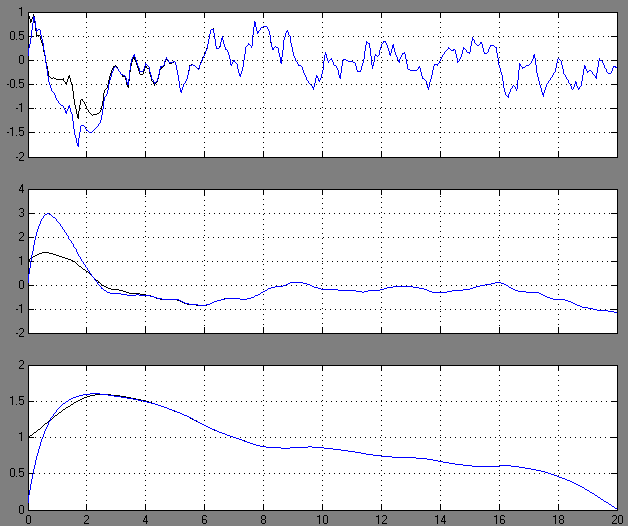
15. Рисунок – Состояние системы 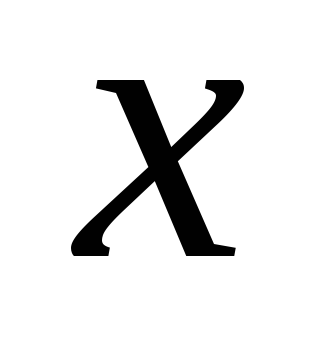(график черного цвета), оценка состояния системы(график синего цвета)

Как видно из рисунка , мы получили совпадение между состоянием системы и оценкой состояния системы.

Реализуем фильтр Бесселя в Matlab:

i1=tf(13, [10 8 1]);

i2=ss(i1);

[A B C D]=ssdata(i2);

%находим матрицу наблюдаемости

Qn=obsv(A,C);

%найдем корни характеристического уравнения

H=poly(A);

H1=roots(H);

Ki=[2.4329-H1(1,1) 2.4662-H1(2,1) 1-H1(3,1)]';

% найдем нормирующую матрицу

Tn=Qn*1;

Tn1=inv(Tn);

% найдем матрицу коэффициентов усиления фильтра

L=Tn1*Ki

An=A-L*C

Реализуем биноминальный полином в качестве наблюдателя в Matlab.

i1=tf(13, [10 8 1]);

i2=ss(i1);

[A B C D]=ssdata(i2);

%находим матрицу наблюдаемости

Qn=obsv(A,C);

%найдем корни характеристического уравнения

H=poly(A);

H1=roots(H);

Ki=[3-H1(1,1) 3-H1(2,1) 1-H1(3,1)]';

% найдем нормирующую матрицу

Tn=Qn*1;

invTn=inv(Tn);

% найдем матрицу коэффициентов усиления фильтра

L=invTn*Ki

An=A-L*C