
- •«Методы оптимизации» для студентов заочной формы обучения
- •Содержание
- •1. Лекционные занятия Модуль 1
- •Тема 1. Введение в методы оптимальных решений
- •Тема 2. Постановка задачи линейного программирования
- •Тема 3. Графический метод решения задачи линейного программирования
- •Тема 4. Симплекс-метод решения задачи линейного программирования
- •Тема 5. Решение задачи линейного программирования на основе теории двойственности
- •Модуль 2
- •Тема 6. Специальные задачи линейного программирования
- •Тема 7. Транспортные задачи
- •Тема 8. Принятие оптимальных решений на основе метода динамического программирования
- •Тема 9. Принятие оптимальных решений на основе методов безусловной оптимизации
- •Тема 10. Принятие оптимальных решений на основе методов условной оптимизации
- •Текст лекций
- •Основные понятия
- •Постановка задачи линейного программирования и свойства ее решений
- •Графический способ решения злп
- •Симплексный метод решение злп
- •Теория двойственности
- •Основные теоремы двойственности и их экономическое содержание
- •Основные виды экономических задач, сводящихся к злп
- •2. Практические занятия Модуль 1
- •Задание 3. Решение задач линейного программирования симплекс-методом
- •Задание 4. Решение задач линейного программирования на основе теории двойственности
- •Задание 5. Решение целочисленных задач линейного программирования на основе метода ветвей и границ
- •Задание 6. Решение транспортных задач на основе метода потенциалов
- •3. Контроль овладения компетенциями
- •4. Самостоятельная работа студентов
- •5.Аттестация Структура аттестации
- •5.1 Примерные вопросы к промежуточному тестированию Модуль 1
- •Модуль 2
- •5.2 Практические задания Модуль 1
- •Модуль 2
- •5.3 Вопросы и задания к итоговой аттестации
- •Модуль 2
- •6.Учебно-методическое обеспечение дисциплины
- •Основная литература
- •6.2 Дополнительная литература
- •7. Информационно-методическое обеспечение дисциплины
- •Контактная информация преподавателя
Задание 3. Решение задач линейного программирования симплекс-методом
Пример. Симплекс-методом решить ЗЛП:
![]() (3.1)
(3.1)
при наличии ограничений:
 (3.1)
(3.1)
![]() ,
,
![]() .
(3.2)
.
(3.2)
Приводим систему
линейных неравенств (3.1) к каноническому
виду, вводя в каждое неравенство
дополнительную переменную
![]() ,
,![]() .
Получим систему линейных уравнений:
.
Получим систему линейных уравнений:
 (3.3)
(3.3)
Целевая функция принимает вид
![]() (3.4)
(3.4)
Расширенная матрица

системы линейных уравнений (3.3) является исходной К-матрицей ЗЛП, которая определяет исходный опорный план:
![]() ,
,
![]() .
.
Кроме того,
![]() .
.
Результаты последовательных итераций симплекс-алгоритма удобно оформить в виде симплекс-таблицы (см. табл. 3.1).
Таблица 3.1
|
S |
i |
|
|
|
3 |
2 |
0 |
0 |
0 |
0 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 | |||||
|
|
|
|
|
|
|
| |||||
|
|
1 2 3 4 |
3 4 5 6 |
0 0 0 0 |
6 8 1 2 |
1 2 -1 0 |
2 1 1 1 |
1 0 0 0 |
0 1 0 0 |
0 0 1 0 |
0 0 0 1 |
6 4 - - |
|
|
|
-3 |
-2 |
0 |
0 |
0 |
0 |
k=1 l=2 | |||
|
|
1 2 3 4 |
3 1 5 6 |
0 3 0 0 |
2 4 5 2 |
0 1 0 0 |
3/2 1/2 3/2 1 |
1 0 0 0 |
-1/2 1/2 1/2 0 |
0 0 1 0 |
0 0 0 1 |
4/3 8 10/3 2 |
|
|
|
0 |
-1/2 |
0 |
3/2 |
0 |
0 |
k=2 l=1 | |||
|
2 |
1 2 3 4 |
2 1 5 6 |
2 3 0 0 |
4/3 10/3 3 2/3 |
0 1 0 0 |
1 0 0 0 |
2/3 -1/3 -1 -2/3 |
-1/3 2/3 1 1/3 |
0 0 1 0 |
0 0 0 1 |
|
|
|
|
0 |
0 |
1/3 |
4/3 |
0 |
0 |
| |||
На второй итерации
S =
2, все
![]() ,
следовательно, опорный план
,
следовательно, опорный план
![]() ,
,
![]() ,
,
определяемый К-матрицей К(2), оптимальный. Тогда
![]() ,
,
![]() .
.
Задания для самостоятельного выполнения
Предприятие
производит 3 вида продукции: А1,
А2,
А3,
используя сырье двух видов: В1
и В2.
Известны затраты сырья i-го
вида на единицу изделия j-го
вида (![]() ),
количество сырья каждого вида
),
количество сырья каждого вида
![]() (i=1,2),
а так же прибыль, полученная от единицы
изделия j-го
вида сj
(j=1,2,3).
(i=1,2),
а так же прибыль, полученная от единицы
изделия j-го
вида сj
(j=1,2,3).
Сколько изделий каждого вида необходимо произвести, чтобы получить: 1) максимум прибыли;
2) максимум товарной продукции?
Обозначения для вариантов: в таблице приведена матрица затрат: А=(аij), справа от таблицы значение bi (i=1,2) и внизу - сj (j=1,2,3).

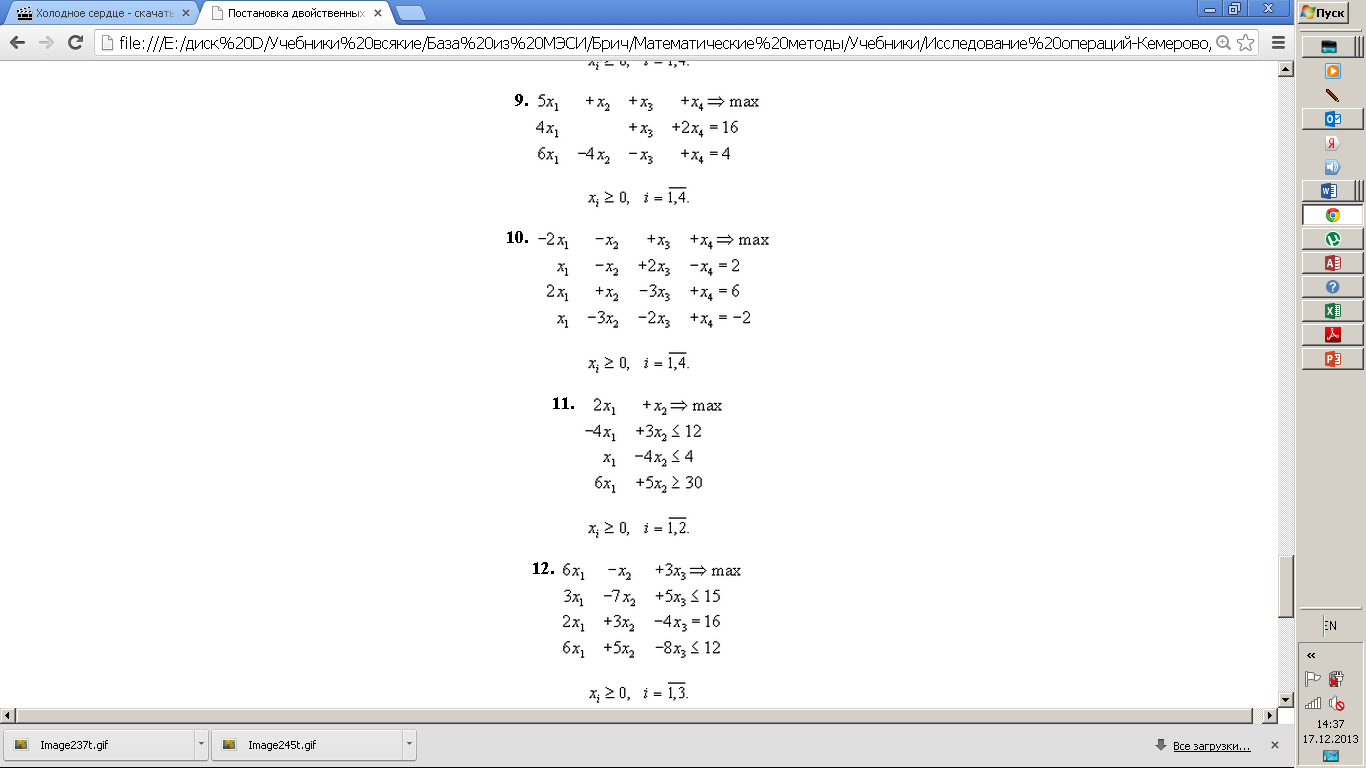
Задание 4. Решение задач линейного программирования на основе теории двойственности
Рассмотрим пример построения двойственных задач.
Пусть прямая задача записана в виде основной ЗЛП:

Каноническая форма прямой задачи примет вид

Двойственная задача примет вид:

Теоремы двойственности позволяют получить оптимальное решение двойственной задачи по известному оптимальному решению прямой задачи.
Пусть есть прямая ЗЛП:

Пусть известно ее прямое решение
![]()
Двойственная задача примет вид :

Т.к. х1
>0, то решение будем искать из первого
ограничения двойственной задачи ![]() .Т.к. первое и третье
ограничение прямой задачи обращается
в строгое неравенство при решении прямой
задачи, то
.Т.к. первое и третье
ограничение прямой задачи обращается
в строгое неравенство при решении прямой
задачи, то ![]() .
.
Таким образом,
![]() .
.
Построить двойственные задачи в соответствии с вариантами:





 0
0
 1
1