
- •Волжская государственная академия водного транспорта
- •Литература
- •2. Основные понятия и сведения
- •Дифференциальные уравнения первого порядка. Теорема существования и единственности решения дифференциального уравнения первого порядка.
- •Некоторые типы уравнений первого порядка.
- •Уравнения второго порядка.
- •Линейные уравнения с постоянными коэффициентами.
- •Возможны случаи:
- •Системы дифференцированных уравнений.
- •Задание на контрольную работу №5.
Дифференциальные уравнения первого порядка. Теорема существования и единственности решения дифференциального уравнения первого порядка.
Если в уравнении у = f (х, у) и ее частная производная ∂ f / ∂у непрерывны в некоторой области D на плоскости х0у, содержащей некоторую точку (х0, у0), то существует единственное решение этого уравнения у = φ (х), удовлетворяющее условию у0 = φ (х0) (это условие называется начальным и его часто записываются в виде у|х = х0 = у0 .
Геометрически теорема означает, что существует единственная функция у = φ (х), являющаяся решением дифференциального уравнения, график который проходит через точку (х0 у0).
Определение 1.1Общим решением дифференциального уравнения первого порядка называется функция у = φ (х, с) удовлетворяющая условиям:
она является решением уравнения при любом значении произвольной постоянной С;
- для любого начального условия у|х = х0 = у0 из области D теоремы существования найдется такое значение С = С0 что решение у = φ (х, с0) удовлетворяет начальному условию, т.е. φ (х, с0) = у0.
Замечание. Часто общее решение получается в неявном виде Ф(х, у, С) = 0, тогда оно называется общим интегралом.
Определение 1.2.Частным решением называется функция у = φ (х, с0) , получающаяся из общего решения при определенном значении С = С0. Аналогично функция Ф(х, у, С) = 0 называется частным интегралом. Задача нахождения частного решения, удовлетворяющего начальному условию, называется задачей КОШИ.
Геометрически частное решение изображается кривой на плоскости (интегральной кривой), а общее решение множеством (семейством) кривых.
Если задано дифференциальное уравнение у' = f (х, у), то в каждой точке плоскости х0у можно найти значение функции f (х, у). Этому значению равна ( в силу дифференциального уравнения) производная от решения в данной точке (угловой коэффициент касательной). Тем самым дифференциальное уравнение в каждой точке задает направление (т.е. поле направлений на плоскости х0у). Интегральная кривая проходит касаясь в каждой точке этого направления.
Пример.Рассмотрим
дифференциальное уравнение у'=![]() .
В точке (1.1) угловой коэффициент касательной
равен f (1.1) = 1. Такой же наклон (tq φ = 1
.
В точке (1.1) угловой коэффициент касательной
равен f (1.1) = 1. Такой же наклон (tq φ = 1![]() φ
φ![]() )
будет во всех точках прямой у = х (f (х,
у) = 1). В точках прямой у = 2х наклон
касательной также будет одинаков и
равен tq φ =
)
будет во всех точках прямой у = х (f (х,
у) = 1). В точках прямой у = 2х наклон
касательной также будет одинаков и
равен tq φ =![]() .
Для этого уравнения нетрудно найти
наклоны касательных и в точках прямых,
проходящих через начало координат.
Таким образом, поле направлений можно
изобразить следующим образом (1 рис.).
.
Для этого уравнения нетрудно найти
наклоны касательных и в точках прямых,
проходящих через начало координат.
Таким образом, поле направлений можно
изобразить следующим образом (1 рис.).
Рис. 1. Изображение одной из интегральных кривых.
Некоторые типы уравнений первого порядка.
1. Уравнения с разделяющимися переменными. Это уравнения, которые можно привести к виду у' = f1(х) * f2 (у). Они решаются разделением переменных: производная записывается как отношение дифференциалов, группируются по разные стороны от знака равенства члена, содержащие х и у соответственно. После интегрирования получается общий интеграл уравнения.
Пример 1.Найти
общий интеграл уравнения у'=![]() .
.
Решение.![]() ln
|у| = ln |х| + ln |с| - общий интеграл ( ln |с| -
произвольная постоянная, записанная в
удобной форме).
ln
|у| = ln |х| + ln |с| - общий интеграл ( ln |с| -
произвольная постоянная, записанная в
удобной форме).![]() |y| = |cx|
|y| = |cx|![]() у = сх – общее решения.
у = сх – общее решения.
Аналогично решаются задачи 1-25.
2. Однородные уравнения. Это уравнение вида у' = f (х, у), где функция f (х, у) обладает свойствами f = (λx, λу) = f (х, у). На основании указанного свойства правой части, с помощью замены переменных у = и * х (вместо функции у (х) вводится новая функция и(х), однородное уравнение сводится к уравнению с разделяющимися переменными.
Пример 2. Найти
общее решение уравнения: у'=![]() ln
ln![]() +
+![]() .
.
Решение.Убеждаемся, что уравнение однородное:
![]() ln
ln![]() +
+![]() =
=![]() ln
ln![]() +
+![]() .
Делаем указанную замену переменных у
= и * х
.
Делаем указанную замену переменных у
= и * х![]() у'= и'х + и (производная
произведения). В новых переменных
уравнение имеет вид и'х + и = иlnи
+ и и решается разделением переменных
у'= и'х + и (производная
произведения). В новых переменных
уравнение имеет вид и'х + и = иlnи
+ и и решается разделением переменных![]() u
u![]()
![]() ln
|lnu| = ln|x| + ln|c|
ln
|lnu| = ln|x| + ln|c|![]() |lnu|
= |cx| lnu = cx
|lnu|
= |cx| lnu = cx![]() u = eсх.
u = eсх.
После возврата к старым переменным общее решение примет вид:
![]() = eсх
= eсх![]() у = х * eсх.
у = х * eсх.
Линейное уравнения. Это уравнение вида у'+ Р (х) * у = Q (х). Будет решать методом вариации произвольной постоянной:
- решается однородное
уравнение у'+ Р (х) * у = 0 , с
разделяющимися переменными![]() =
- Р (х) dx
=
- Р (х) dx![]() у – с *
у – с *![]() ,
,
- произвольная
постоянная С считается функцией с (х)
и эта функция подбирается из условия,
чтобы у = с(х) *
![]() была бы решением исходного неоднородного
уравнения; этот подбор сводится к решению
еще одного уравнения с разделяющимися
переменными относительно искомой
функции с (х). После подстановки ч = с(х)
*
была бы решением исходного неоднородного
уравнения; этот подбор сводится к решению
еще одного уравнения с разделяющимися
переменными относительно искомой
функции с (х). После подстановки ч = с(х)
*![]() в уравнение имеем
в уравнение имеем![]() +
Р(х)
+
Р(х)![]() =
Q (х)
=
Q (х)![]() с' = Q (х)
с' = Q (х)![]()
![]() с =
с =![]() Q (х)
Q (х)![]() dx + с1.
dx + с1.
Окончательно
общее решение имеет вид: у = (![]() Q (х)
Q (х)![]() dx + С1
)
dx + С1
)
![]() .
.
Пример.3.
Кривая проходит через точку (1.3), угловой
коэффициент касательной к этой кривой
в любой ее точке зависит от координат
точки касания следующим образом: к
(х, у) =
![]() - х . Найти уравнение этой кривой.
- х . Найти уравнение этой кривой.
Решение.
Из
геометрического смысла производной,
для нахождения уравнения кривой можно
записать: у1
=
![]() - х.
- х.
Частное решение этого уравнения, удовлетворяющее условию : у (1) = 3, дает уравнение искомой кривой:
у1 =
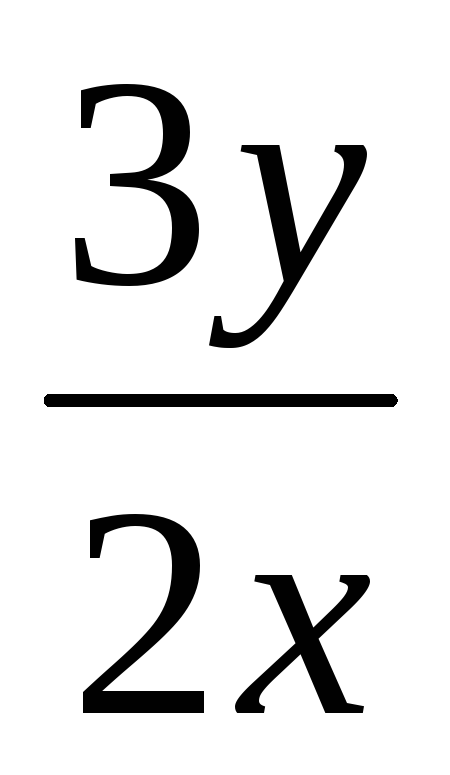

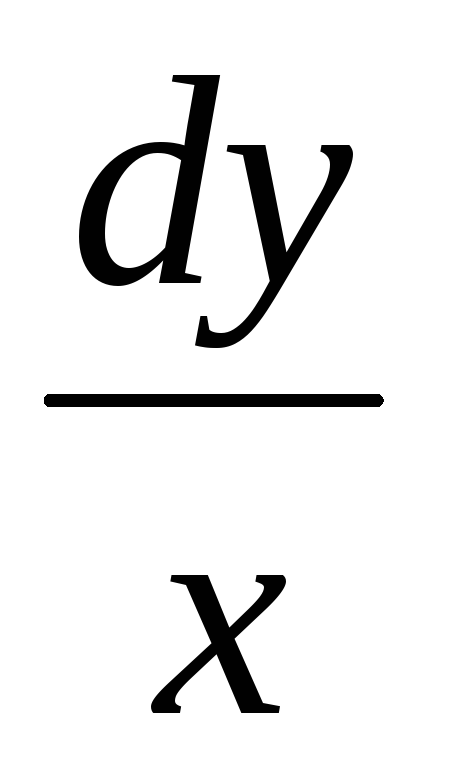 =
=
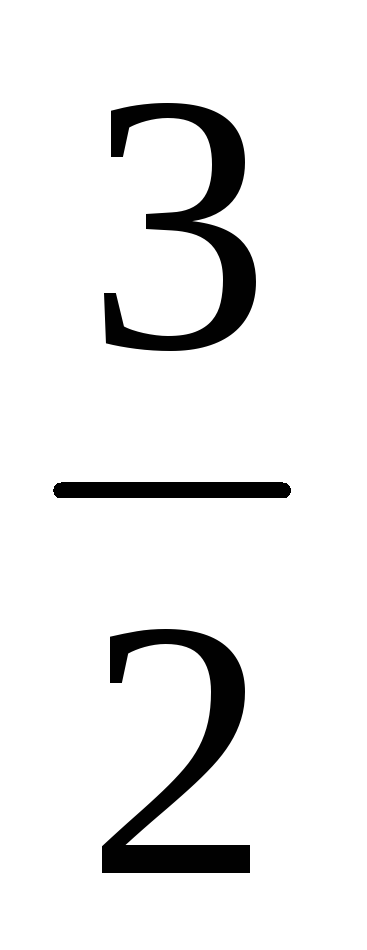
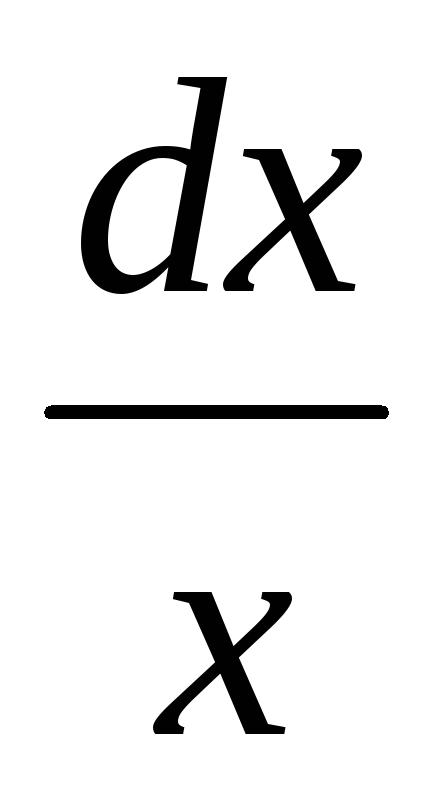
 ln|y|
ln|y|
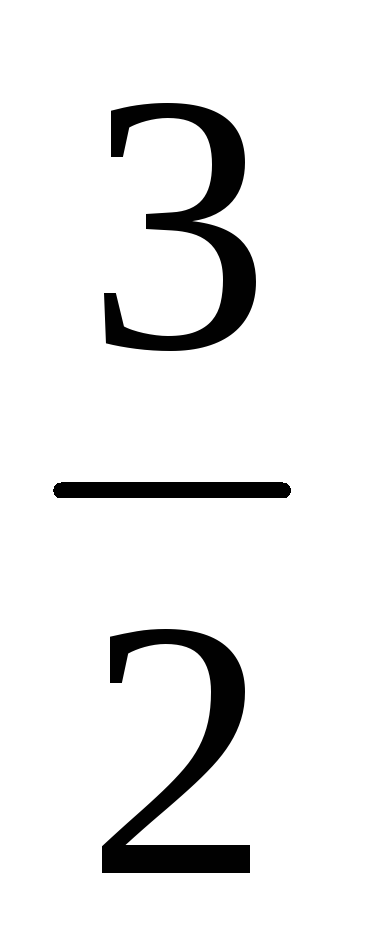 ln |х| + ln |с|
ln |х| + ln |с| у = с
у = с .
.у = с(х) *
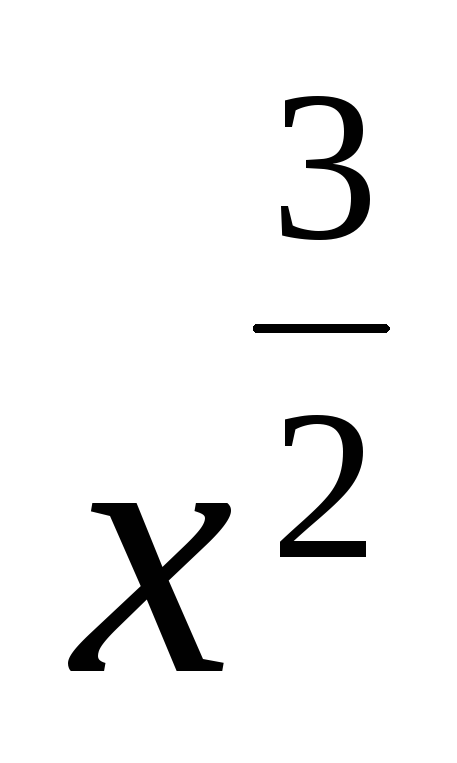
 с'
с'
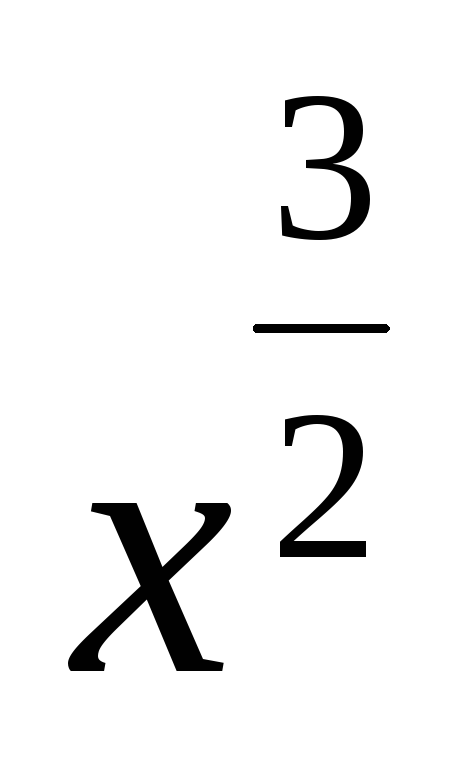 + с *
+ с *
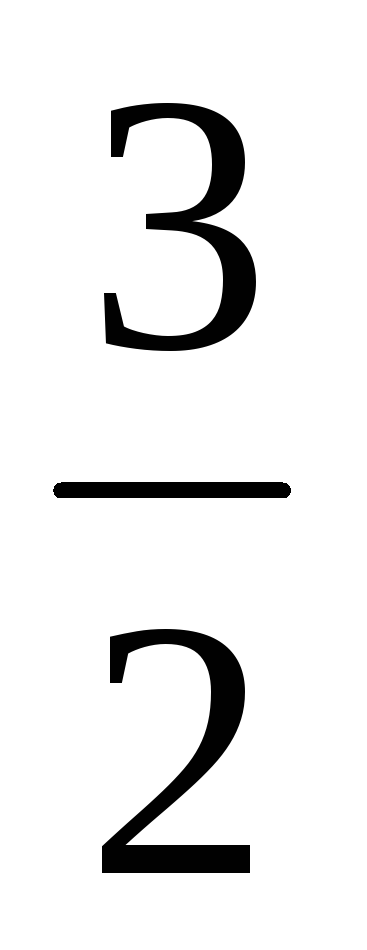
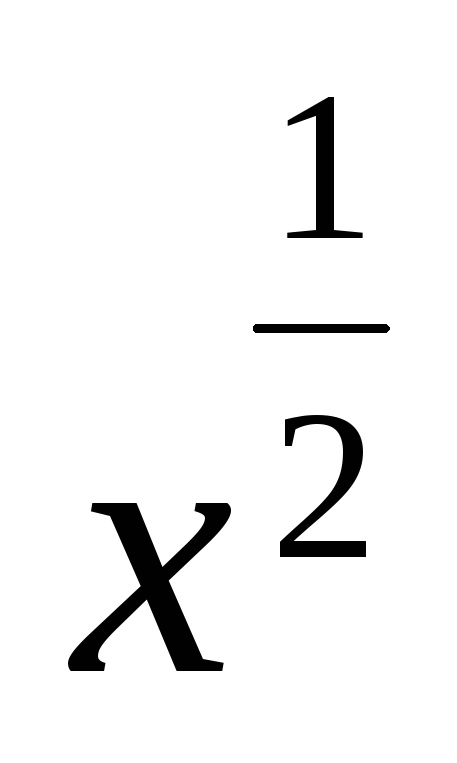 =
=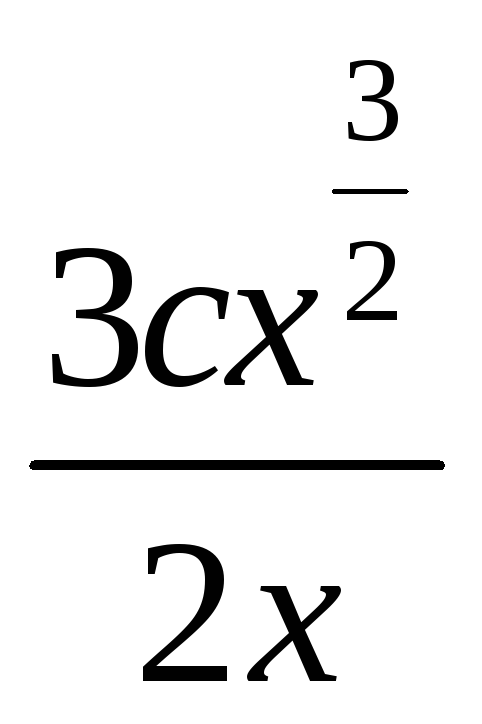 -
х
-
х с' =
с' =
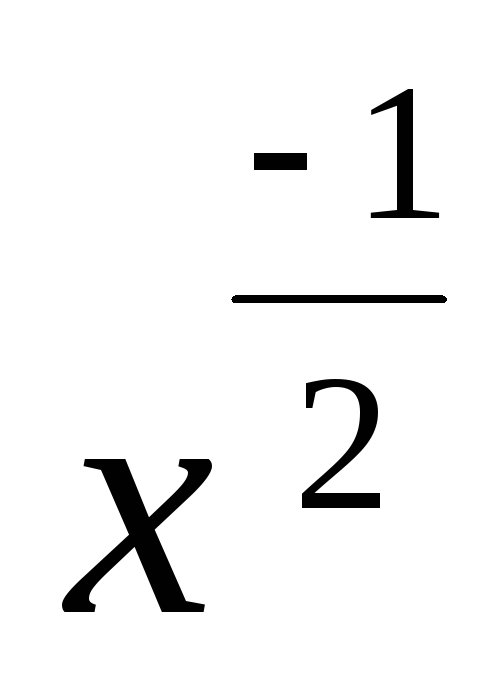
 с = -2
с = -2 + с1.
+ с1.
Общее
решение дифференциального уравнения
имеет вид: у = (с1
- 2![]() )
)![]() - 2х2.
- 2х2.
Из
начального условия у (1) = 3 подберем
произвольную постоянную С1
. Имеет 3 = С1
– 2 ![]() С1
= 5.
С1
= 5.
Таким
образом, уравнение искомой кривой имеет
вид: у = 5![]() - 2х2.
- 2х2.
Аналогично решается задачи 26 – 50.
