5. Уравнения второго порядка.

1. Уравнения, допускающие понижения порядка.

1. Уравнения вида у" = f(х) решается последовательным интегрированием.

Пример. Решить уравнение у" = sin х.

Решение.

у' = sin х dх у' = - cos х + С₁ у = (- cos х + с₁) dх = - sin х + с₁ х + с₂.

2. Уравнения вида у" = f(х , у') после замены переменных у' = Р (х) сводятся к уравнениям первого порядка.

Пример.2. Решить уравнение у" = ln+.

Решение. у' = Р (х) у" = Р' (х); Р' (х) = ln+.

Получилось уравнение первого порядка, решенное в примере 2.1., где получено решение вида Р = с₁х. Возвращаясь к исходным переменным, получаем дифференциальное уравнение первого порядка:

= с₁ х у = с₁ + с₂.

3.Уравнения вида у" = f(у, у') после замены переменных вида у' = Р (у) сводятся к уравнениям первого порядка относительно функции Р(у) аргумента у.

Пример 3. Решить уравнение: у" = у + 1.

Решение.

Делаем замену у' = Р (у) у" *

(по правилу дифференцирования сложной функции). Тогда данное уравнение приводится к виду * Р = у + 1 – уравнение первого порядка с разделяющимися переменными. Поэтому: Рd Р = (у + 1)dу =+ у + Р = .

Возвращаемся к старым переменным и получаем еще одно уравнение с разделяющимися переменными:

= = dх =dх ln | у + 1 + | = х + С₂ .

2. Линейные уравнения с постоянными коэффициентами.

Это уравнения вида у" + Ру' + qу = f(х). Общее решение этого неоднородного уравнения есть сумма общего решения у₀однородного уравнения (f(х) = 0) и любого частного решениянеоднородного уравнения, т.е. у = у₀+.

Общее решение однородного уравнения записывается после нахождения корней соответствующего характеристического уравнения К²+ рк + q = 0.

Возможны случаи:

- корни действительны и различны (к₁ ≠ к₂), тогда у₀ = с₁ е^к1х + с₂ е^к2х;

• корни действительные кратные (к₁ = к₂ = к), тогда у₀ = (с₁ + с₂ х) е ^кх;

• корни комплексно сопряженные (к_1,2 = α ± iβ), тогда у₀ = е^αх (с₁ соs βх + с₂ sin βх).

Частное решение для рассматриваемых видов правых частей можно найти подбором неизвестных коэффициентов:

• если правая часть имеет вид f (х) = Р_п (х) е^ах (Р_п (х)- известный многочлен степени п), то 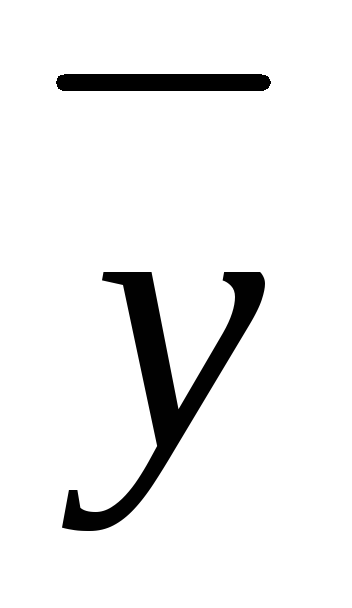ищется в виде = 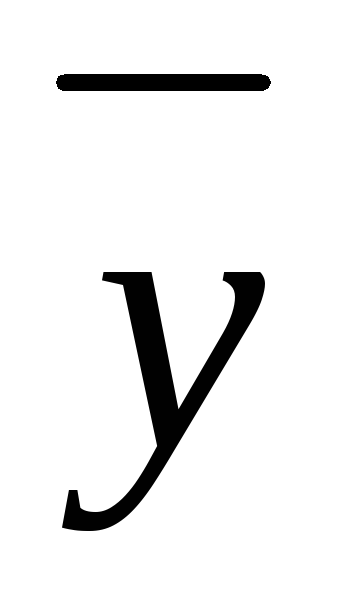Q_п(х) е^ах , если а ≠ к₁ и а ≠ к₂ (здесь и далее Q_п(х) это многочлен степени п, коэффициенты которого и необходимо подобрать); 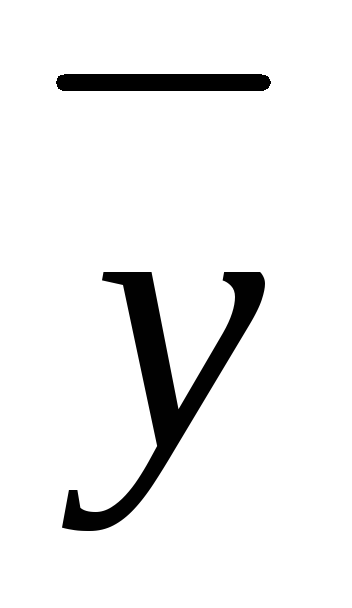= х Q_п(х) е^ах , если α совпадает с одним из корней характеристического уравнения; 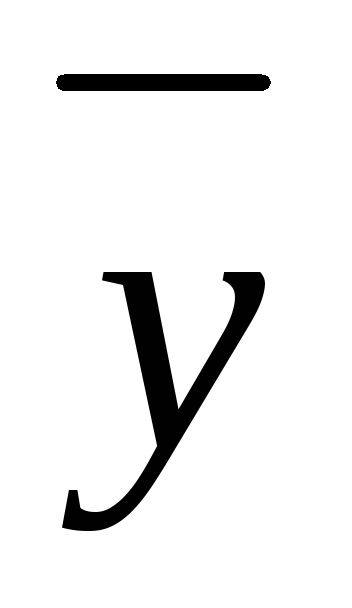= х² Q_п(х) е^ах , если а = к₁ = к₂;

• если правая часть уравнения имеет вид f (х) = А соs Вх + В sin Вх, то 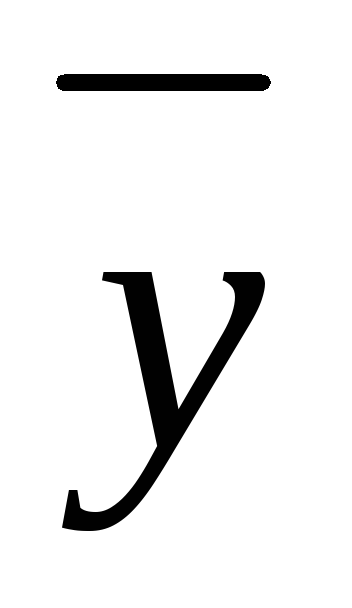имеется в виде 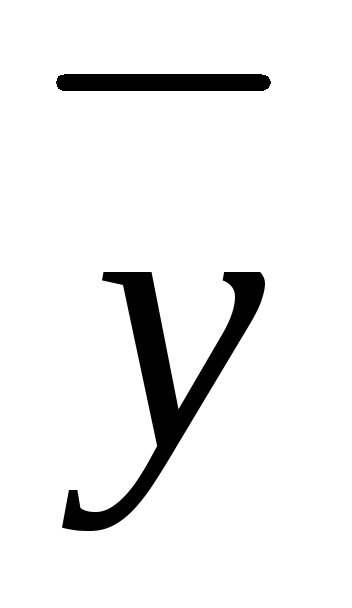= х(М соs Вх + N sin Вх), если корни характеристического уравнения

к_1,2 = α ± iβ; = М соs Вх + N sin Вх во всех остальных случаях.

Пример 1. Найти частное решение уравнения: у" – 4у' + 3у = (х + 2)е^х , удовлетворяющее начальным условиям у (0) = 0, у' (0) =

Решение.

Характеристическое уравнение имеет вид к² – 4к – 3 = 0, а его корни к₁ = 1 и к₂ = 3. Следовательно, у₀ = с₁ е^х + с₂ е^3х.

Так как коэффициент при х в показателе экспоненты правой части уравнения равен одному из корней характеристического уравнения (α = 1), то частное решение ищется в виде: = х(Ах + В) е^х .

Коэффициенты А и В следует подобрать таким образом, чтобы после подстановки в левую часть уравнения это левая часть тождественно равнялась бы его правой части (х + 2) е^х . Подстановку в уравнение удобно осуществлять в следующей форме:

3	= (Ах^2 + Вх)е^х
+ -4	= е^х (Ах^2 + Вх)+ е^х (2 Ах + В)
+ 1	= е^х (Ах^2 + Вх)+2 е^х (2 Ах + В) + е^х 2А

Е^х [х² (4А – 4А) + х(3В – 4В – 8А + В + 4А)+ (-4В + 2В + 2А)] = (х + 2)е^х.

Из полученного тождества следует система линейных уравнений относительно А и В:

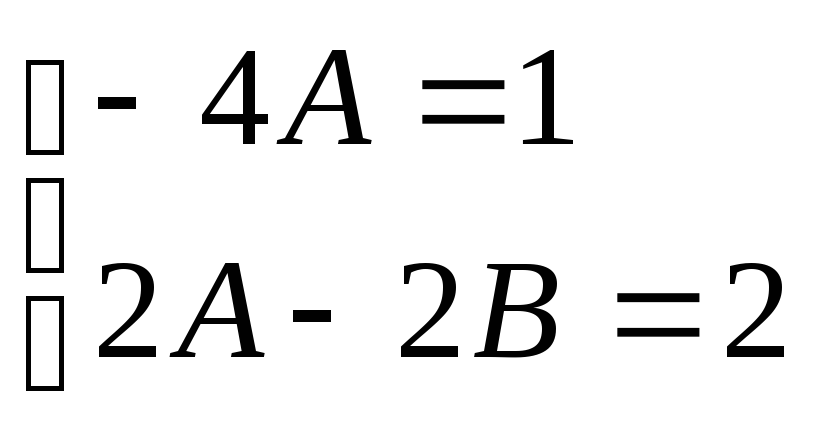
откуда: А = - , В = -.

Следовательно, общее решение дифференциального уравнения имеет вид:

у = с₁ е^х + с₂ е^3х – (х² +х) е^х.

для нахождения частного решения, удовлетворяющего начальным условиям (решения задачи Коши), найдем у':

у' = с₁ е^х + 3с₂ е^3х – е^х (х² +х) е^х (х +).

Из начальных условий получаем систему:

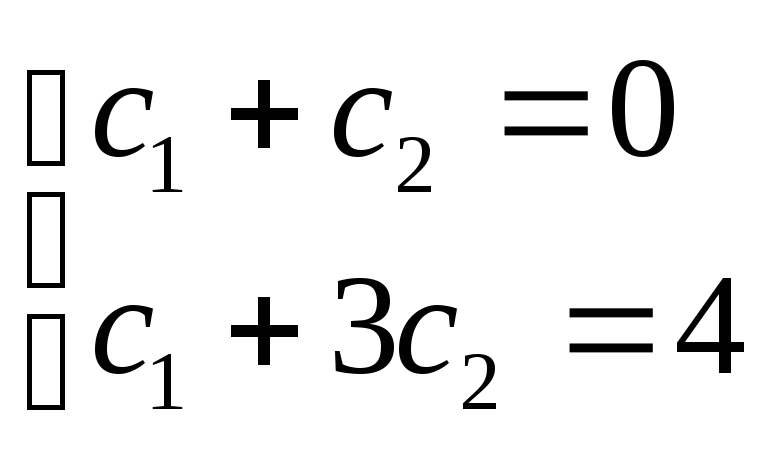
ее решением будет с₁ = -2; с₂ = 2. Поэтому окончательно частное решение, удовлетворяющее начальным условиям, имеет вид:

у = -2а^х + 2е^3х – е^х (х² +х).

Аналогично решаются задачи 51-75.