2. Основные теоремы о пределах функций.

Пусть а-число или один из символов ∞; -∞;+∞.

Теорема1. Предел от постоянной величины равен этому постоянному:

Теорема2. Если функция f(x) и g(x) имеют конечный предел, то .

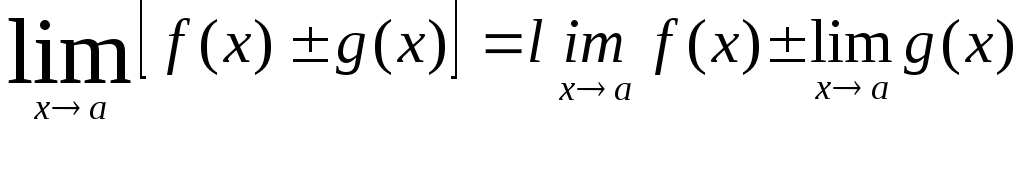Теорема3. Если функция f(x) и g(x) имеют конечный предел, то .

Теорема4. Если функция f(x) и g(x) имеют конечный предел, то .

Теорема5. Если в окрестности точки а выполняется неравенство

.

Теорема 6. Функция не может иметь более одного предела.

Бесконечно малые функции и их свойства.

Определение. Функция f(x) называется бесконечно малой при х→а (а – число или один из интервалов ∞, +∞, -∞), если .

Пример: Функция y=sin x, при х→0 бесконечно малая, т.к. .

Теорема. Число А является пределом функции y=f(x) при х→а, тогда и только тогда, если в окрестности точки а выполняется условие f(x)=A+λ(x). где λ(x) →0, при x →а.

Теоремы о бесконечно малых

Теорема1. Сумма фиксированного числа бесконечно малых при x →а функций есть функция бесконечно малая при x →а.

Теорема2. Произведение фиксированного числа бесконечно малых функций при x →а есть функция бесконечно малая при x →а.

Теорема3. Произведение функции бесконечно малой при x →а, на функцию, ограниченную в окрестности точки а, есть функция бесконечно малая

при x →а.

Теорема4. Частное от деления бесконечно малой функции на функцию предел которой при x →а конечен и отличен от нуля, есть функция бесконечно малая.

Бесконечно большие функции

Определение. Предел функции f(x) при х→а (а – число) равен бесконечности, если для любого числа Е>0, существует δ>0, такое, что для всех х, удовлетворяющих условию выполняется неравенство. Обозначается.

a x a x a x

Свойства бесконечно больших величин.

1) Произведение бесконечно больших функций при х→а есть функция бесконечно большая при х→а.

2) Сумма бесконечно больших функций при х→а одного знака, есть функция бесконечно большая при х→а.

3) Произведение бесконечно больших функций при х→а на функцию, имеющую конечный предел отличный от нуля, есть функция бесконечно большая при х→а.

4) Сумма бесконечно большой функции на функцию ограниченную в окрестности точки а , есть функция бесконечно большая при х→а.

5) Частное от деления бесконечно большой функции на функцию, имеющую конечный предел при х→а, есть функция бесконечно большая при х→а.

Определение. Предел функции f(x) при х→а равен +∞, если

, такое, что для всех х принадлежащих δ окрестности выполняется условие

Определение. Предел функции f(x) при х→а, равен -∞, если , такое что для всех х, удовлетворяющих условию, выполняется неравенство.

Определение. Предел функции f(x) при х→∞ равен - ∞, если такое, что для всех х, удовлетворяющих условию, выполняется неравенство

Теорема. (связь функций бесконечно малых и бесконечно больших) Если функция f(x) бесконечно малая при х→а и f(x) ≠0, в окрестностях точки а, то функция бесконечно большая при х→а, и обратно, если функция f(x), бесконечно большая при х→а, то функция бесконечно малая при х→а.

Теоремы о пределах.

1. Функция имеет не более одного предела. Пусть y=f(x) имеет два предела при х→а: .

По теореме (1) f(x)=A+α(x), где α(x)→0.

(2) f(x)=B+β(x), где β(x)→0.

Рассмотрим (1) – (2) 0=А+ α(x)-В- β(x) следовательно В – А = α(x) - β(x), т.к. α(x) - β(x) – есть бесконечно малая функция при х→а, а В – А – число не равное нулю, по условию, то быть равными они не могут, значит наше предположение не верно. Функция имеет не более одного предела.

2. Предел алгебраической суммы двух функций при и х→а, равен алгебраической сумме пределов этих функций при х→а.

;

3. Предел произведения двух функций имеющих конечный предел при х→а, равен произведению пределов этих функций при х→а.

.

4. Предел от постоянной функции при х→а равен значению этих функций. у=с. . С – константа.

5. Постоянный множитель можно выносить за знак предела.

6. Предел частного двух функций при х→а, равен частному пределов этих функций при х→а, если предел делителя не равен нулю, т.е.

.

7. Если сложная функцияy=f(u),

, то предел сложной функции .

Сравнение бесконечно малых величин.

Пусть α(x); β(x);γ(x) – функции бесконечно малые при х→а. ( а – число или ∞; +∞; - ∞). Бесконечно малые функции часто сравниваются по быстроте стремления к нулю. Рассмотрим бесконечно малые величины

Если мы сравним друг с другом более далекие значения наших бесконечно малых величин, то заметим, что они приближаются к нулю с разными скоростями.

.

Ясно, что быстрее, чем,абыстрее, чем.

Определение. Если предел отношения прих→а равен нулю, то говорят, что α – бесконечно малая более высокого порядка, чем β.

Определение. Если предел отношения прих→а конечен и отличен от нуля, то α и β называются бесконечно малыми одного порядка малости.

Определение. Если предел отношения прих→а равен ∞, то говорят, что α(х) бесконечно малая низшего порядка малости, по сравнению с β(х)

Чтобы сравнить две бесконечно малые величины необходимо найти предел их отношения.

Не всякие бесконечно малые величины можно сравнить между собой.

- не существует.

Если предела отношения двух бесконечно малых величин не существует, то говорят, что эти бесконечно малые величины не сравнимы.

Определение. Две бесконечно малые величины называются эквивалентными, если предел их отношения равен 1.

- эквивалентные бесконечно малые величины.

Теорема. При раскрытии неопределенности вида можно и числитель и знаменатель этой неопределенности заменить величинами им эквивалентными.

Два замечательных предела.

Лемма. Если , то справедливо неравенство(ά в радианах).

Теорема. Предел отношения синуса бесконечно малого угла к величине этого угла в радианах равен 1.

.

2) Второй замечательный предел.