3. Проверка гипотезы об однородности двух или более

анализируемых совокупностей

Пусть мы имеем несколько наборов данных (выборок), образованных в результате наблюдения за одним и тем же параметром интересующего нас объекта. Эти наборы могут быть образованы, например, за счёт разделённости их регистрации во времени и в пространстве.

я выборка:

я выборка

(1) -----------------------------------------

-----------------------------------------

я выборка .

Обозначим функцию распределения, описывающую вероятностный закон, которому подчиняю наблюдения, первой выборки через , второй выборки черези т.д.

Основные гипотезы однородности можно записать в следующем виде:

(2)

(3)

(4)

В случае принятия неотрицательного результата проверки этих гипотез утверждают, что соответствующие выборки однородны, т.е. принадлежат одной генеральной совокупности и различаются статистически незначительно. Это означает, что условия регистрации выборочных данных можно считать неизменными.

4. Проверка гипотез о законе распределения

Для статистической проверки гипотез о виде распределения вероятностей исследуемой случайной величины используется критерия согласия

(5)

где параметры проверяемого закона распределения.

Во многих случаях закон распределения изучаемой случайно вели­чины неизвестен, но есть основания предположить, что он имеет вполне определенный вид: нормальный, биномиальный или какой-либо дру­гой.

Пусть необходимо проверить гипотезу о том, что с. в. X под­чиняется одному из законов распределения, функция, распределения которой, , т. е. : Под альтернативной гипо­тезой будем понимать в данном случае то, что просто не выполнена основная гипотеза, т.е.H₁: .

Для проверки гипотезы о распределении случайной величины X проведем выборку, которую представим в виде статистического ряда:

			…
			…

где объем выборки.

Требуется сделать заключение: согласуются ли результаты наблю­дений с высказанным предположением. Для этого используем специ­ально подобранную величину так называемую «критерий согласия».

Критерием согласияназывают статистический критерий проверки гипотезы о предполагаемом законе неизвестного распределения. (Он используется для проверки согласия предполагаемого вида распреде­ления с опытными данными на основании выборки.)

Существуют различные критерии согласия: Пирсона. Колмогорова, Фишера, Смирнова и др.

Критерий согласия Пирсона — наиболее часто употребляемый кри­терий для проверки простой гипотезы о законе распределения.

5. Критерий согласия ( Критерия Пирсона)

Для проверки гипотезы поступают следующим образом. Разбивают всю область значений св.Xнаmинтервалов и подсчитывают вероятности ,попа­дания случайной величины(т.е. наблюдения) в интервал, используя формулу

Тогда теоретическое число значений с.в. X, попавших в интервал, можно рассчитать по формуле. Таким образом, имеем статистический ряд распределения с. в. X (8.11) и теоретический ряд распределения:

		…
		…

Если эмпирические частоты () сильно отличаются от теоретиче­ских частот (), то проверяемую гипотезу следует отвергнуть; в противном случае нужно принять.

Каким критерием, характеризующим степень расхождения между эмпирическими и теоретическими частотами, следует воспользовать­ся? В качестве меры расхождения между и для

К. Пирсон (1857-1936; английский математик - философ) пред­ложил величину «критерий Пирсона» в следующем виде:

(6) .

Согласно теореме Пирсона, при статистика (6) имеетраспределение с степенями свободы, гдет — число групп (интервалов) выборки, г — число параметров предполагаемого распределения. В частности, если предполагаемое распределение нормально, то оценивают два параметра(а и), поэтому число степеней свободы.

Правило применения критерия сводится к следующему:

1. По формуле (6) вычисляют - выборочное значение статистики критерия.

2. Выбрав уровень значимости α критерия, по таблицераспределения находим критическую точку (квантиль).

3. Если гипотеза не противоречит опытным данным; то гипотезаН₀ отвергается.

Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений Если в отдельных интервалах их меньше, то число интервалов надо уменьшить путем объединения (укрупнения) соседних интервалов.

Пример 2. Измерены 100 обработанных деталей; отклонения от за­данного размера приведены в таблице:

	[-3, -2)	[-2, -1)	[ -1, 0)	[ 0 , 1)	[1, 2)	[ 2, - 3)	[ 3, 4)	[ 4, 5)
	3	10	15	24	25	13	7	3

Проверить при уровне значимости гипотезу о том, что отклонения от проектного размера подчиняются нормальному закону распределения.

Решение.Число наблюдений в крайних интервалах меньше 5, поэтому объединим их с соседними. Получим следующий ряд распределения :

	[-3,-1)	[-1, 0)	[0, 1)	[1, 2)	[2, 3)	[3,5)
	13	15	24	25	13	10

Случайную величину — отклонение — обозначим через X. Для вычисления вероятностей необходимо вычислить параметры, определяющие нормальный закон распределения (аи ). Их оценки вычислим по выборке:

.

Находим . Так как св.определена на, то крайние интервалы в ряде распределения заменяем, соот­ветственно, наи. Тогда

Аналогично по­лучаем:

р₂= 0,1667,р₃= 0,2258,р₄= 0.2183,р₅= 0,1503,

Полученные результаты приведем в следующей таблице:

	(- ∞, - 1)	[ - 1, 0)	[ 0, 1)	[ 1, 2)	[ 2, 3)	[ 3, + ∞)
	13	15	24	25	13	10
	13,14	16,67	22,58	21,83	15,03	10,75

Вычисляем :

.

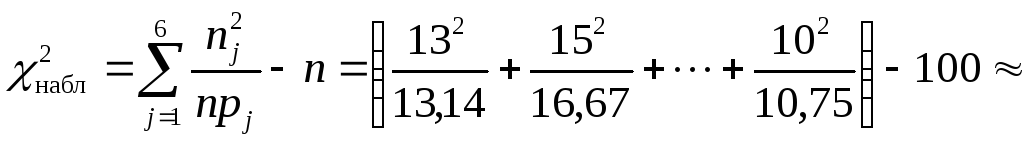
Следовательно,

Находим число степеней свободы, по выборке рассчитаны два параметра, значит, r = 2. Количество интервалов 6, т. е.m= 6. Следо­вательно,k= 6 -2-1 = 3. Зная, чтоα= 0,01 ик= 3, по таблице- распределения находим. Итак,, следовательно, нет оснований опровергнуть проверяемую гипотезу. Таким образом, отклонения от заданного размера подчиняются нормальному закону распределения.