1

Линейные пространства

     Определение линейного пространства

     Пусть V - непустое множество (его элементы будем называть векторами и обозначать ...), в котором установлены правила:

     1) любым двум элементам соответствует третий элемент называемый суммой элементов (внутренняя операция);

     2) каждому и каждому отвечает определенный элемент (внешняя операция).

     Множество V называется действительным линейным (векторным) пространством, если выполняются аксиомы:

     I.

     II.

     III. (нулевой элемент, такой, что ).

     IV. (элемент, противоположный элементу ), такой, что

     V.

     VI.

     VII.

     VIII.      Аналогично определяется комплексное линейное пространство (вместо R рассматривается C).

2

Линейная комбинация называетсятривиальной, если все коэффициенты равны нулю одновременно:

Линейная комбинация называетсянетривиальной, если хотя бы один из коэффициентов отличен от нуля.

Ненулевые векторы называютсялинейно зависимыми, если нетривиальная линейная комбинация этих векторов равнанулевому вектору:

Пример

Ненулевые векторы называютсялинейно независимыми, если только тривиальная линейная комбинация этих векторов равна нулевому вектору.

3

Ба́зис — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

Множество Lназывается линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:

1. Каждой паре элементов xиyизLотвечает элементx+y изL, называемый суммой xиy, причём:

x+y=y + x − сложение коммутативно;

x+(y+z)=(x + y) + z − сложение ассоциативно;

x+ 0 =x− существует единственныйнулевойэлемент0 (x+ 0 =xдля любогоxизL);

x+ (−x) = 0− для каждого элементаxизL существует единственный противоположный элемент−x ( x + (−x) = 0 для любогоxизL).

2. Каждой паре xиα, гдеα− число, аxэлемент изL, отвечает элементα·x, наываемыйпроизведением α и x, причём:

α·(β·x) = (α·β)·x− умножнение на число ассоциативно:;

1·x=x − для любого элементаxиз L.

3. Операции сложения и умножения на число связаны соотношениями:

α·(x + y) = α·x + α·y− умножнение на число дистрибутивно относительно сложения элементов;

(α + β)·x = α·x + β·x− умножнение на вектор дистрибутивно относительно сложения чисел.

x = x₁·i + x₂· j,   y = y₁·i + y₂· j,

x + y = (x₁+ y₁)·i + ( x₂+ y₂)· j,   α·x = (αx₁)·i + (αx₂)· j,

0= 0·i+ 0·j,   −x= (−x₁)·i+(−x₂)·j.

Справедливость остальных аксиом линейного пространстваследует из свойств операций сложения и умножения на число действительных чисел.

4

Преобразование координат вектора при преобразовании базиса

Пусть

^

A

:Xn → Xn — линейный оператор. Зададим в Xn два базиса: "старый" базис e = (e1, e2,  … , en) и "новый" базис f = (f1, f2,  … , fn) .

Матрицей перехода от базиса e к базису f называется матрица C = (cik)    (i,k = 1, … ,n) , столбцами которой являются координатные столбцы векторов f1, f2,  … ,fn в базисе e , т.е.

f1 = c11 e1 + c21 e2 + … + cn1 en, f2 = c12 e1 + c22 e2 + … + cn2 en, … … … … … …  , fn = c1n e1 + c2n e2 + … + cnnen,

или в матричной форме:

f = eC

(1)

где C — матрица перехода

C =

ж з з з з и

c11	c12	…	c1n
c21	c22	…	c2n
…	…	…	…
cn1	cn2	…	cnn

ц ч ч ч ч ш

Замечание. В силу линейной независимости базисных векторов матрица C — невырожденная ( det C ≠ 0 ). Следовательно, C имеет обратную матрицу C − 1 .

Теорема 1. Преобразование координат вектора при переходе от "старого" базиса e к "новому" базису fопределяется формулой:

X\f = C − 1X\e.

(2)

Доказательство. Обозначим координатные столбцы произвольного вектора x О Xn в "старом" базисе e

Xe =	ж з з з з и	x1 x2 … xn	ц ч ч ч ч ш

и в "новом" базисе f

Xf =	ж з з з з и	x'1 x'2 … x'n	ц ч ч ч ч ш

Произвольный вектор x в базисе eимеет вид:

x = eXe

(3)

В базисе f тот же вектор имеет вид:

x = fXf

и в силу формулы (1)

x = eCXf.

(4)

Сравнивая формулы (3) и (4), получаем

X\e = C · Xf.

Умножая это равенство слева на C −1 , получаем формулу (2), которую требовалось доказать.

¾¾¾¾   *   *   *   ¾¾¾¾

5

Подпространства линейного пространства Определение линейного подпространства

Непустое подмножество линейного пространства называетсялинейным подпространствомпространства , если

1) (подпространство замкнуто по отношению к операции сложения);

2) и любого числа (подпространство замкнуто по отношению к операции умножения вектора на число).

Для указания линейного подпространства будем использовать обозначение , а слово "линейное" опускать для краткости.

6

Пересечение и сумма подпространств линейного пространства

Пусть и — подпространства линейного пространства .

Пересечением подпространств и называется множество векторов, каждый из которых принадлежит и одновременно, т.е. пересечение подпространств определяется как обычное пересечение двух множеств.

Алгебраической суммой подпространств и называется множество векторов вида , где . Алгебраическая сумма (короче просто сумма) подпространств обозначается

Представление вектора в виде , где , называется разложением вектора no подпространствам и .

Пересечение и сумма

Пусть и —подпространствавекторного пространства надполем .

Предложение 1.Пересечение подпространств и является векторным пространством.

Замечание 1.Объединение пространств и не обязано быть векторным пространством, как показано в следующем примере.

Пример 1.Пусть , то есть множество векторов вида , где .Базисомэтого пространства служат вектора и . Положим и —линейные оболочкивекторов и , соответственно. Сумма векторов не содержится в .

Определение 1.Суммой¹⁾подпространств и называется наименьшее подпространство в , содержащее и , то есть

.

Вообще говоря, можно определить сумму любого конечного числа подпространств:

Определение 1'.Сумма подпространств в — это наименьшее подпространство, содержащее все , то есть

.

Предложение 2.Пусть и — подпространстваконечномерноговекторного пространства . Тогда

.

7

РАНГ СИСТЕМЫ ВЕКТОРОВ

Рассмотрим систему векторов (1.1), где . Максимальной линейно независимой подсистемой системы векторов (1.1) называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы (1.1) линейно выражается через векторы этого набора. В общем, система векторов (1.1) может иметь несколько разных максимальных линейно независимых подсистем.

8.1

Евклидово пространство

Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3.

В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно -мерное евклидово пространство обозначается , хотя часто используется не вполне приемлемое обозначение .

1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:

,

в простейшем случае (евклидова норма):

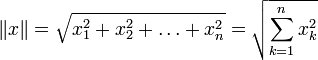
где (в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).

2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:

,

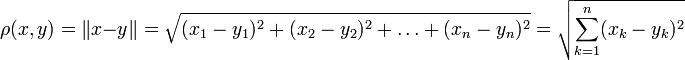где и .

3. Вообще любое предгильбертово пространство (пространство со скалярным произведением ).

8.2

Скаля́рное произведе́ние иногда внутреннее произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

Обычно предполагается, что скалярное произведение положительно определено, то есть

для всех .

Если этого не предполагать, то произведение называется индефинитным (неопределенным).

8.3

Норма—функционал, заданный навекторном пространствеи обобщающий понятиедлинывектораилиабсолютного значения числа.