Собственные числа и собственные векторы линейного оператора

Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует. Пусть дано линейное пространство R_nи действующий в нем линейный оператор A; в этом случае оператор A переводит R_nв себя, то есть A:R_n→ R_n.

Определение.Ненулевой вектор называется собственным вектором оператора A, если оператор A переводит в коллинеарный ему вектор, то есть . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору . Отметим некоторые свойства собственных чисел и собственных векторов. 1. Любая линейная комбинация собственных векторов оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом. 2. Собственные векторы оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_mлинейно независимы. 3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется nлинейно независимых собственных векторов , соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: тогда . Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A. Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема.Матрица линейного оператора A в базисе (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса - собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Пусть дан вектор , где x₁, x₂, …, x_n- координаты вектора относительно базиса и - собственный вектор линейного оператора A, соответствующий собственному числуλ, то есть . Это соотношение можно записать в матричной форме

. (*)

Уравнение (*) можно рассматривать как уравнение для отыскания , причем , то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A - λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A - λE) = 0. Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1) где - матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Получили уравнение для нахождения собственных чисел. Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду. Пусть λ₁, λ₂, …, λ_n- вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример 12.Линейный оператор A действует в R₃по закону , где x₁, x₂, .., x_n- координаты вектора в базисе , , . Найти собственные числа и собственные векторы этого оператора.Решение.Строим матрицу этого оператора: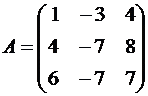. Составляем систему для определения координат собственных векторов:Составляем характеристическое уравнение и решаем его:. λ_1,2= -1, λ₃= 3. Подставляя λ = -1 в систему, имеем:или Так как , то зависимых переменных два, а свободное одно. Пусть x₁- свободное неизвестное, тогда Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как n - r = 3 - 2 = 1. Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: , где x₁- любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x₁= 1: . Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: . В пространстве R₃базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R₃составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.

Пример 13.Дана матрица . 1. Доказать, что вектор является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору. 2. Найти базис, в котором матрица A имеет диагональный вид.Решение.1. Если , то - собственный вектор. Вектор (1, 8, -1) - собственный вектор. Собственное число λ = -1. Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные. Собственные векторы ищем из системы:Характеристическое уравнение: ; (3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ²- 1) = 0 λ₁= -3, λ₂= 1, λ₃= -1. Найдем собственный вектор, отвечающий собственному числу λ = -3:Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x₁= x₃= 0. x₂здесь может быть любым, отличным от нуля, например, x₂= 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:. Если λ = 1, то получаем систему Ранг матрицы равен двум. Последнее уравнение вычеркиваем. Пусть x₃- свободное неизвестное. Тогда x₁= -3x₃, 4x₂= 10x₁- 6x₃= -30x₃- 6x₃, x₂= -9x₃. Полагая x₃= 1, имеем (-3,-9,1) - собственный вектор, отвечающий собственному числу λ = 1. Проверка:. Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R₃. Таким образом, в базисе , , матрица A имеет вид:. Не всякую матрицу линейного оператора A:R_n→ R_nможно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.

Определение.Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой .Замечания.1. Все собственные числа симметрической матрицы вещественны. 2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны. В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Матрица линейного преобразования в базисе из собственных векторов

В разделе "Матрица линейного преобразования" мы выяснили, что каждое линейное преобразование -мерного линейного пространства в фиксированном базисе задается матрицей. Если меняется базис, то, как правило, меняется и матрица. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного преобразования имеет наиболее простой вид. В общем случае выбрать такой базис довольно сложно. Это связано с нахождением нормальной жордановой формы матрицы, изложение которого можно найти в более обстоятельных учебниках по линейной алгебре, например, в [4], [5]. Следующая теорема отвечает на этот вопрос в более простом случае.

        Теорема 19.2   Пусть  -- линейное преобразование -мерного линейного пространства. Матрица линейного преобразования имеет диагональный вид

(19.5)

тогда и только тогда, когда векторы базиса являются собственнными векторами преобразования , соответствующими собственным числам .

        Доказательство.     Пусть преобразование имеет линейно независимых собственных векторов , соответствующих собственным числам . Так как векторы линейно независимы, то они образуют базис. Найдем матрицу преобразования в этом базисе. Ее первый столбец является координатным столбцом вектора . Так как  -- собственный вектор, то

Координатный столбец этого вектора . Второй столбец матрицы является координатным столбцом вектора . Так как  -- собственный вектор, то

Координатный столбец этого вектора . Вычисляя аналогично остальные столбцы, получаем, что матрица линейного преобразования в базисе имеет вид  (19.5). Первая часть теоремы доказана.

Пусть в некотором базисе матрица линейного преобразования имеет вид (19.5). Найдем образ вектора . Этот вектор имеет координатный столбец , его образ имеет координатный столбец

Следовательно,  -- собственное число преобразования , а  -- соответствущий ему собственный вектор. Аналогично находим, что любой базисный вектор является собственным вектором преобразования , соответствующим собственному числу .     

        Следствие 19.2   Если у матрицы порядка существует набор из линейно независимых собственнных векторов, соответствующих собственным числам , то матрица подобна диагональной матрице с числами на диагонали.

        Теорема 19.3   Пусть собственные векторы преобразования соответствуют собственным числам , среди которых нет равных друг другу. Тогда система векторов является линейно независимой.

        Доказательство.     Воспользуемся методом математической индукции по числу векторов. Если , то утверждение теоремы следует из того, что собственный вектор -- ненулевой.

Пусть утверждение верно для системы векторов . Составим линейную комбинацию векторов и приравняем ее к нулю

(19.6)

К обеим частям применим преобразование

По определению линейного преобразования получим

Так как  -- собственные векторы, то

Умножим равенство (19.6) на и вычтем из последнего равенства. Получим

Так как по предположению индукции векторы линейно независимы, то

По условию , следовательно, . Подставим эти значения в (19.6), получим . Получили, что из равенства (19.6) следует , то есть векторы линейно независимы.     

        Следствие 19.3   Если матрица порядка имеет попарно различных собственных чисел, то она подобна диагональной матрице.