Ортогонализация

По любой линейно независимойсистеме можно построить ортонормированную систему, применивпроцесс ортогонализации Грама ― Шмидта.

Любая полная линейно независимая система в конечномерном пространстве является базисом. От простого базиса, следовательно, можно перейти к ортонормированному базису.

Ортогональное разложение

При разложении векторов векторного пространствапо ортонормированному базису упрощается вычисление скалярного произведения: , где и .

Ортонормированный базис

Определение. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.

            Определение. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат.

            Пример. Даны векторы(1; 2; 3), (-1; 0; 3), (2; 1; -1) и (3; 2; 2) в некотором базисе. Показать, что векторы ,  и  образуют базис и найти координаты вектора  в этом базисе.

            Векторы образуют базис, если они линейно независимы, другими словами, если  уравнения, входящие в систему:

           линейно независимы.

Тогда .

Это условие выполняется, если определитель матрицы системы отличен от нуля.

    Для решения этой системы воспользуемся методом Крамера.

 

₁ =

;

₂ =

 

₃ =

Итого, координаты вектора в базисе , , :    { -1/4, 7/4, 5/2}.

Ортогональные системы векторов

 

Определение.Система ненулевых векторов называется ортогональной, если все векторы этой системы попарно ортогональны.

Теорема.Ортогональная система ненулевых векторовлинейно независима.

11

Ортогонализация

По любой линейно независимойсистеме можно построить ортонормированную систему, применивпроцесс ортогонализации Грама ― Шмидта.

Любая полная линейно независимая система в конечномерном пространстве является базисом. От простого базиса, следовательно, можно перейти к ортонормированному базису.

Ортогональное разложение

При разложении векторов векторного пространствапо ортонормированному базису упрощается вычисление скалярного произведения: , где и .

12

Ортогональное дополнение

Ортогональное дополнениеподпространства векторного пространства сбилинейной формой — это множество всех векторов ,ортогональныхкаждому вектору из . Это множество является векторным подпространством , которое обычно обозначается .

Определение

Пусть —векторное пространствонадполем сбилинейной формой . Вектор ортогонален слева вектору , а вектор ортогонален справа вектору тогда и только тогда, когда Левое ортогональное дополнение подпространства — это множество векторов, ортогональных слева каждому вектору , то есть

Аналогичным образом определяется правое ортогональное дополнение. Для симметричнойиликососимметричнойбилинейной формы поэтому определения левого и правого ортогонального дополнения совпадают.

Определение можно перенести на случай свободного модулянадкоммутативным кольцом.^[1]

Свойства

• Ортогональное дополнение является подпространством, то есть замкнуто относительно сложения векторов и умножения на элемент поля.

• Если , то

• Радикал билинейной формыявляется подпространством любого ортогонального дополнения.

• 

• Если форма 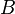являетсяневырожденной, а пространство конечномерно, то

• Если же 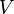— конечномерноеевклидово пространствои — скалярное произведение (или жеунитарное пространствои эрмитово скалярное произведение соответственно), то для любого подпространства разлагается впрямую сумму и ^[2]

Пример

Пусть — двумерное пространство с базисом , иматрица билинейной формыв этом базисе имеет вид Тогда ортогональное дополнение подпространства, натянутого на вектор — это множество таких векторов что Например, ортогональное дополнение пространства, натянутого на вектор , совпадает с ним самим, тогда как ортогональное дополнение натянуто на вектор .

13