Тема 8. Непрерывная случайная величина.

Основные определения и формулы :

Случайная величина называется непрерывной(НСВ), если ее функция распределенияF(x) непрерывна при любомхи имеет производнуюF’(x) везде, кроме, может быть, конечного числа точек.

Плотностью распределенияНСВ Х называется производная ее функции распределения:f(x) =F’(x).

Свойства плотности НСВ Х:

1. f (x)  0;

2. 

3. 

4. P(x < X < x+x)  f (x)x ;

5. Если P(a < X < b) = 1, то f (x) = 0 вне [a; b].

Для НСВ вводятся те же числовые характеристики, что и для ДСВ. В формулах для их вычисления суммы заменяются интегралами, например:

М(Х) =

причем, требуется, чтобы написанный несобственный интеграл сходился абсолютно.

Для НСВ Х вводится еще одна характеристика – медиана Ме(Х) – следующим равенством:

Р(Х < Me(X)) = P(X > Me(X)).

Решение типовых примеров :

Пример 1.НСВ Х задана плотностью распределения:

f(x) =

Найти: а) параметр к; б) функцию распределения; в) числовые характеристики; г) вероятность Р(|Х – М(х)| <(х)); д) вероятность того, что в 10 независимых наблюдениях СВ Х ровно 7 раз примет положительные значения.

Решение :

а) Неизвестный параметр плотности обычно находят, используя одно из ее свойств:

б) Связь между плотностью и функцией распределения устанавливается с использованием еще одного свойства плотности:

Для нашей задачи имеем:

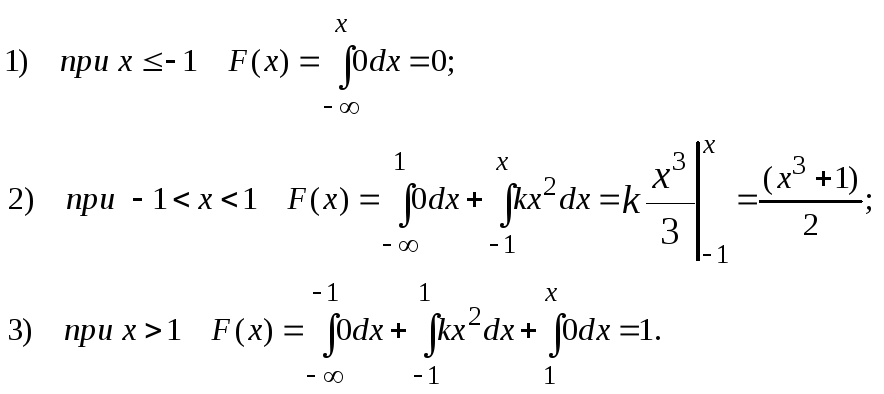
Итак, получили:

Значения 0 и 1 для F(x) вытекают из общих ее свойств:

Если СВ Х принимает значения только на промежутке [а; b] ,то левее а F(x) = 0 и правее b F(x) = 1.

в) находим числовые характеристики:

7) Мода для НСВ – это точка максимума плотности распределения. В нашей задаче такой точки нет, а есть, напротив, точка минимума: х = 0. Такое распределение называют антимодальным.

8) Медиана  формально находится из равенства:

Геометрически медиана – это точка, в которой площадь под плотностью делится пополам. Т.к. наше распределение симметрично относительно х = 0, то медиана = 0. Кстати, равенство М(х) = 0 также следует из этой симметрии.

д) Каждое из 10 наблюдений СВ Х – это испытание, в котором может появиться событие А = {x> 0}. Вероятность этого события:

Тогда искомая вероятность семи положительных значений в 10 наблюдениях есть:

Пример 2.На окружности радиусаRс центром в начале координат наудачу выбирается точка. Ее абсцисса – некоторая НСВ Х. Найти М(Х²).

Решение :

Точка выбирается на окружности наудачу, т.е. можно считать, что полярный угол Uэтой точки есть НСВ, равномерно распределенная на промежутке [0, 2]. Ее плотность распределения:

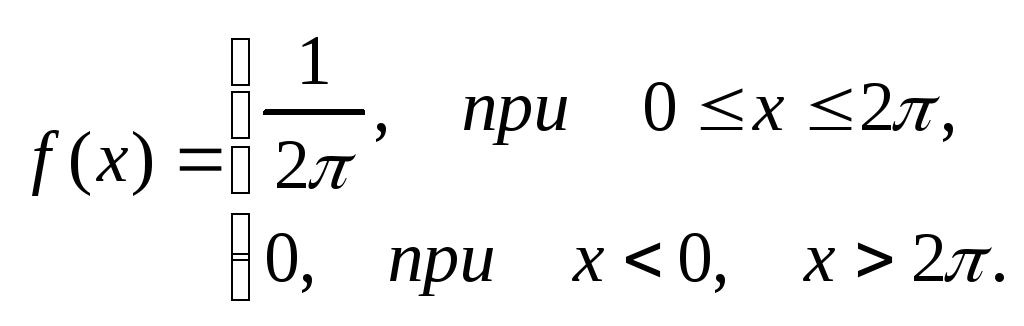
Точка имеет полярные координаты (R; U), поэтому ее абсциссаx = R cos(U). Итак, требуется найти М(R²cos²U). Используем следующее свойство математического ожидания: если НСВUимеет плотность распределенияf(x), аg(x) – некоторая функция, то:

В нашем случае имеем:

Тема 9. Нормальное распределение.

Основные определения и формулы:

Говорят, что НСВ Х имеет нормальное распределениес параметрамити, если ее плотность имеет вид:

Основные числовые характеристики: М(Х) = m,D(X) =². Вероятность того, что такая СВ примет значение в некотором интервале, выражается через функцию Лапласа:

Для интервала, симметричного относительно т:

Если в последней формуле положить а = 3, то получим:

Отсюда следует так называемое “правило 3^хсигма”:

нормально распределенная с параметрами т и  случайная величина практически всегда принимает значения из промежутка (т – 3 ; т + 3).

Решение типовых примеров:

Пример 1.Дозатор-автомат фасует сахар в мешки по 50 кг. Неизбежные случайные ошибки в работе дозатора приводят к тому, что масса наудачу взятого мешка есть СВ Х, имеющая нормальное распределение со средним значениемт = 50 кг.известно, что 1,5% мешков имеют массу, превышающую 51 кг. а) Каков % мешков, масса которых меньше 49,5 кг.? б) Какова вероятность того, что среди 7 наудачу выбранных мешков ровно 1 будет иметь массу меньше 49,5 кг.?

Решение :

Рассмотрим событие А={X > 51}. По условию задачи Р(А) = 0,015. С другой стороны:

Сравнивая, получим (1/)=0,475. Из таблицы значений функции Лапласа находим, что значение 0,475 она принимает в точке 2,17. Отсюда получаем:

Таким образом, 14% всех мешков имеют массу меньше 49,5 кг.

Находя значения функции Лапласа, мы пользовались ее свойствами: 1) нечетность; 2)стремление к 05 при неограниченном возрастании аргумента.

б) выбор мешка – это испытание, в котором может произойти событие A={X < 49,5}, причем р = Р(А) = 0,14. Используем формулу Бернулли:

Пример 2.Имеется случайная величина Х, подчиненная нормальному закону с параметрамити. Требуется приближенно заменить нормальный закон равномерным в интервале (a;b), причем, его границы подобрать так, чтобы сохранить неизменными основные числовые характеристики СВ Х: математическое ожиданиети дисперсию².

Решение :

Известно, что, если НСВ Х имеет равномерное распределение на (a;b), то ее характеристики есть:

Требование задачи состоит в следующем:

Решая эту систему, получим:

Пример 3.Случайная величина Х имеет нормальное распределение с математическим ожиданиемт = 0. Найти значение среднего квадратичного отклонения, при котором вероятность попадания СВ Х в данный интервал (a;b),a> 0, достигает максимума.

Решение :

Выразим вероятность попадания в интервал через функцию Лапласа:

Чтобы исследовать на максимум, требуется найти производную и приравнять ее к нулю. Вспоминая правило дифференцирования определенного интеграла по верхнему пределу и правило дифференцирования сложной функции, получим:

Равенство этой производной нулю означает, что

Или

Отсюда имеем выражение для критической точки:

Выясним характер этой точки. Вероятность P(a<X<b) как функцияположительна и определена на (0; +), причем, при стремлениик каждому из концов этого интервала, эта вероятность стремится к 0 (следствие непрерывности функции Лапласа). Значит, найденная критическая точка может быть только точкой максимума.