matametika_bevz_standart_1 / matametika_bevz_standart

2 Ðîçäië

Зазначимо основні властивості тригонометричних функцій. Функція у = sin х. Її область визначення – множина всіх дійсних чисел R, а область значень – відрізок [–1; 1]. Функція непарна, періодична, її найменший додатний період дорів-

нює 2π. Графік функції зображено на малюнку 68.

Функція у = соs х. Її область визначення – множина всіх дійсних чисел R, область значень – відрізок [–1; 1]. Функція парна, періодична, її найменший додатний період дорівнює 2π. Графік функції у = соsх зображено на малюнку 70.

Функція у = tg х. Її область визначення – множина всіх дійс? них чисел, за винятком значень 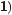, де n Z, область

значень – множина R. Функція непарна, періодична, її найменший додатний період дорівнює π. Графік функції у = tg х складається з безлічі рівних між собою нескінченних і центрально?симетричних ліній (мал. 71). Графік функції у = tgх називають тангенсоїдою.

Мал. 71

Функція у = ctg х. Її область визначення – множина всіх дійсних чисел, за винятком значень х = πn, де n Z, область значень – множина R. Функція непарна, періодична, її найменший додатний період дорівнює π. Графік функції у = ctgх складається з безлічі рівних між собою нескінченних і центрально?симетричних ліній (мал. 72).

Мал. 72

112

ВЛАСТИВОСТІ І ГРАФІКИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ §14

Інші властивості тригонометричних функцій (нулі, проміжки знакосталості, зростання і спадання) можна прочитати за відповідними графіками. Спробуйте це зробити самостійно.

Для порівняння всі властивості функцій зведено в одну таблицю (всюди k Z). Із часом усі вони будуть обґрунтовані і ви навчитеся визначати їх аналітично.

Таблиця

f(x)

у = sin х

у = cos х

у = tg х

у = ctg х

D(y)

(–∞; +∞)

(–∞; +∞)

х ≠

+ πk

х ≠ πk

Е(у)

[–1; 1]

[–1; 1]

(–∞; +∞)

(–∞; +∞)

непарна

парна

непарна

непарна

Т

2π

2π

π

π

у = 0

πk

+ πk

πk

+ πk

у > 0

(2πk; π + 2πk)

у< 0

(–π + 2πk; 2πk)

у ↑

(–π + 2πk; 2πk)

–

у ↓

(2πk; π + 2πk)

–

(πk; π + πk)

Знаючи, який вигляд має, наприклад, графік функції у = соsх, можна побудувати графік функції у = 3 + соsх (мал. 73).

у = 3 + соs х

у = соsх

Мал. 73

113

2Ðîçäië

Адивлячись на графік, можна вказати й основні властивості функції у = 3 + соs х. Її область визначення – множина R, об-

ласть значень – відрізок [2; 4]. Функція парна, періодична з найменшим додатним періодом 2π.

ПЕРЕВІРТЕ СЕБЕ

1.Яку функцію називають періодичною?

2.Назвіть область визначення і множину значень кожної з тригонометричних функцій.

3.Назвіть основний період кожної з тригонометричних функцій.

4.Чи мають нулі тригонометричні функції?

5.Як називаються графіки основних тригонометричних функцій?

1.	Побудуйте графік функції:
а)	у = 3sinх; б) у = 3sin2х; в) у = sin(х + 2).

Р о з в ’ я з а н н я. a) Щоб побудувати графік функції у = 3sinх (див. с. 33), треба графік функції у = sin х розтягнути від осі х у 3 рази (мал. 74). Чому?

б) Щоб побудувати графік функції у = sin2х (див. с. 35), треба графік функції у = sinх стиснути до осі у вдвічі (мал. 75).

у= 3sin х

у= sin х

Мал. 74
у = sin2х	у = sin х

Мал. 75

114

ВЛАСТИВОСТІ І ГРАФІКИ ТРИГОНОМЕТРИЧНИХ ФУНКЦІЙ §14

в) Щоб побудувати графік функції у = sin (х + 2), треба графік функції у = sinх перенести на 2 одиниці вліво (мал. 76).

у = sin х

у = sin(х + 2)

Мал. 76

Так само можна перетворювати й інші графіки тригонометричних функцій. Поясніть ці перетворення самостійно.

521.Поясніть, як змінюється значення функції у = sinх при збільшенні її аргументу х від 0 до 2π.

522.Як змінюється значення функції у = cos х і у = tg х при збільшенні їх аргументу x від 0 до 2π?

523.Чи можна вважати парною функцію у = cosх, задану на множині (0; +∞)? А на множині [–π; π]?

524.Чи можна вважати непарною функцію у = sin х, задану на множині [–2π; 2π]? А на множині [0; +∞)?

525.Чи можна вважати непарною функцію у = cos(х – 1), задану на [0; 20π]? А на [–20π; 20π]?

À

Побудуйте графік функції (526–533).

526.	а) у = sinх, х [–π; π];	б) у = cosх, х [–π; 3π].
527.	а) у = 1 + cosх, х [0; 2π];	б) у = sinх – 2, х [–2π; 2π].
528.	а) у = tgх, х (0; 2π);	б) у = –1 + tgх, х (–π; π).

529.а) у = sin(х + 1), х [–π; π]; б) у = cos(х – 1), х [0; 2π].

530.у = 4sinх на [–π; π].

531.у = –0,5cosх на [–π; π].

532.у = sin3х на [–3; 3].

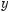
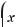
533. на [0; 2π].

534.Знайдіть область визначення функції:

а)						; б)		; в) у = tg3х; г) у = cos(2х + 3).

115

2Ðîçäië

535.Знайдіть область значень функції:

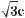
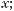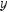
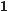
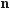
а) у = 2sinх; б) в) 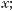г) у = –17tgх.

Á

536.								Чим відрізняється графік функції у = tg х, заданої на
										від графіка функції у = х3?
537.								Знайдіть абсциси точок перетину графіка функції
y = sin										з віссю х.

538.Знайдіть абсциси точок перетину графіків функцій

у= соs2х і у = 0,5.

539.Парною чи непарною є функція:

а) у = sin2х;

б) у = 3cоsх;

в) у = –tgх;

г)

ґ)

д)

540. Як можна побудувати графік функції:

а)

б) у = соs2 х + sin2 х;

в) у =

г) у = tgх ctgх?

Побудуйте графік і визначте основні властивості функцій

(541–546).
541.	а) у = 3 + sinх;	б) у = 2 + соsх;	в) у = 3 + tgх.
542.	а) у = –sinх;	б) у = –соsх;	в) у = –tgх.
543.	а) у = 1 – sinx;	б) у = 1 – соsх;	в) у = 1 – tgх.
544.	а) у = 2sinx;	б) у = 3соsх;	в) у = 0,5tgх.
545.	а) у = |sinx|;	б) у = |соsх|;	в) у = |tgх|.
546.	а) у = sin|x|;	б) у = соs|х|;	в) у = tg|х|.
547.	Чи правильно, що графік функції						є також

графіком функції у = sinx?

548.Чи правильно, що графік функції у = |1 + соs х| є також графіком функції у = 1 + соsх?

549.Розв’яжіть рівняння:

а) х2 – 7|х| = 0;

б) х2 + 3|х| – х = 0.

550. Спростіть вираз:

116

ПЕРІОДИЧНІ ФУНКЦІЇ І ГАРМОНІЧНІ КОЛИВАННЯ §15

551. Заробітна плата токаря становила 2000 грн. Спочатку її було збільшено на 10 %, а потім через рік – ще на 20 %. На скільки відсотків збільшилася заробітна плата токаря порівняно з початковою?

§ 15. Періодичні функції і гармонічні коливання

Кожному добре відомі явища, що чергуються: ранок, день, вечір, ніч, ранок, день...; весна, літо, осінь, зима, весна, літо...

І маятник годинника коливається так, і струна, і значення змінного струму, і багато механізмів працюючої машини змінюють своє положення періодично і плавно. Математичне моделювання таких явищ і процесів зручно здійснювати за допомогою формули гармонічного коливання.

Коливання – ритмічні переміщення чого?небудь з одного боку в інший, зміна значень величини тощо. Можна говорити про коливання маятника, коливання температури повітря, коливання цін тощо. Коливання бувають різними, зокрема вільними, вимушеними, затухаючими (наведіть відомі вам приклади

зфізики). Особливо цікаві гармонічні коливання – періодичні, здійснювані за законом синуса чи косинуса. Коротше їх назива-

ють гармоніками.

Як змінюватиметься значення функції у = sin х, якщо значення аргументу х рівномірно збільшувати? Від такої зміни значення y гармонійно коливатиметься (на осі у) у межах від –1 до 1. Це – найпростіший приклад гармонічного коливання

замплітудою 1. Приклад гармонічного коливання з амплі-

тудою А, здійснюваного залежно від зміни часу t, дає формула у = A sint.

Розглянемо загальний випадок. Нехай точка М рухається

по колу радіуса А в додатному напрямі зі сталою кутовою швидкістю ω радіанів за секунду (мал. 77).

Якщо в початковий момент часу (тобто коли t = 0) точка М займала положення М0, яке визначається кутом ϕ, то через t секунд вона займе деяке положення М, яке визначається кутом ωt + ϕ. Ордината точки М дорівнює Asin(ωt + ϕ).

Формула у = Asin (ωt + ϕ) визначає змінну у як функцію часу t. Це і є форму-

ла гармонічного	коливання. У ній
у – значення функції, t – аргумент, а числа
А, ω і ϕ – сталі:	Мал. 77

117

2 Ðîçäië

А – амплітуда коливання,	ϕ – початкова фаза,
ω – кутова швидкість,	ωt + ϕ – фаза коливання.

Амплітуда визначається в лінійних одиницях довжини, фаза і початкова фаза – у радіанах.

Амплітуда – це величина найбільшого відхилення від положення рівноваги.

Період Т гармонічного коливання – це найменший додатний період функції у = A sin(ωt + ϕ), тобто час, протягом якого точка М здійснює один повний оберт по колу. За цей час точка М проходить ωТ радіанів, або 2π радіанів. Якщо ω > 0, то

ωТ = 2π, звідси .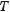

Період гармонічного коливання визначається в секундах; він обернено пропорційний кутовій швидкості відповідного обертання; не залежить ні від амплітуди, ні від початкової фази коливання. Приклади простіших графіків гармонічних коливань – на малюнках 74–76.

Г р а ф і к гармонічного коливання

у = Asin(ωt + ϕ),

де А, ω і ϕ – дані числа, будують у такій послідовності: а) спочатку будують графік функції у = sinх;

б) стисненням до осі у у відношенні 1 : – дістають графік функції у = sinωх;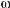

в) із цього графіка за допомогою паралельного перенесення

на відстань вправо при ϕ < 0 і вліво при ϕ > 0 дістають графік

функції у = sin(ωx + ϕ);

г) нарешті, з графіка цієї функції стисненням до осі х у від?

ношенні k = дістають графік заданої функції у = Asin(ωx + ϕ).

Існують періодичні функції, відмінні від гармонічних коливань. Такою є, наприклад, функція у = tg x (мал. 71). Узагалі, періодичними є всі функції виду Asin (ωx + ϕ), Acos (ωx + ϕ), Atg (ωx + ϕ), Actg(ωx + ϕ) та багато інших.

Період перших двох функцій знаходиться за формулою ,

а двох других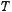

Періодичною є також функція, графік якої – кардіограма здорової людини (див. мал. 15). Періодичними бувають не тільки функції та їхні графіки, а й багато інших зображень: вишивки, орнаменти, візерунки на тканинах чи шпалерах тощо (мал. 78). Такими є, зокрема, давньогрецькі орнаменти меандр і акант (мал. 79), візерунки на огорожах тощо. Усе це – приклади

118

ПЕРІОДИЧНІ ФУНКЦІЇ І ГАРМОНІЧНІ КОЛИВАННЯ §15

Мал. 78

Мал. 79

стрічкових орнаментів, періодичних в одному напрямі. А є також площинні орнаменти, періодичні в багатьох різних напрямах.

Подібні площинні орнаменти особливо поширені в країнах ісламу. Але – без зображень людей та інших живих істот, адже Коран забороняє створювати такі зображення: «Не створи собі кумира!» А голландський художник М. Ешер, ігноруючи цю заборону, створив багато оригінальних орнаментів із зображень людей і тварин. Такою є, наприклад, його мозаїка «Рицарі на конях» (мал. 80).

Мал. 80

119

2	Ðîçäië
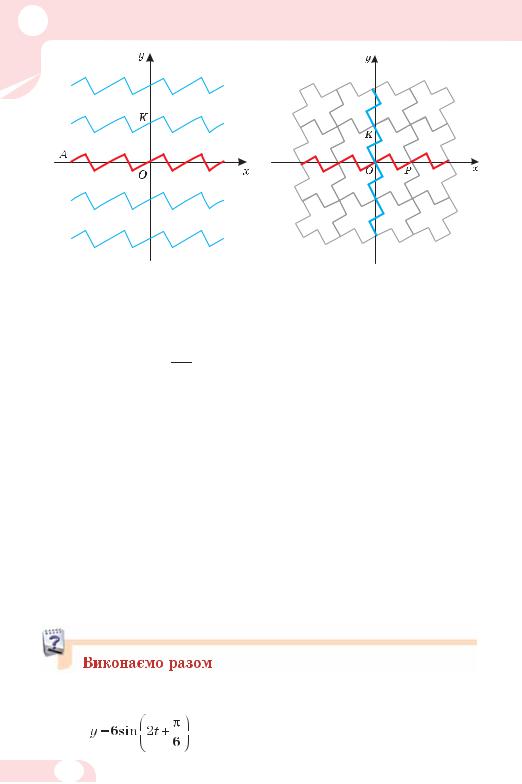
	Мал. 81

Мал. 82

Як можна створювати такі площинні орнаменти і паркети з рівних фігур? Розглянемо один спосіб.

Розгляньте періодичну функцію, графіком якої є нескінченна в обидва боки ламана А (мал. 81). Перенісши її вздовж осі ординат на вектор n 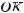, де n пробігає множину всіх цілих чисел, утворимо безліч подібних графіків періодичних функцій. Якщо всі ці ламані повернути навколо початку координат на прямий кут, утвориться ще одна множина ламаних, яка з першою множиною розбиває всю площину на безліч періодично розташованих хрестоподібних фігур (мал. 82). Таким способом рівними періодичними лініями можна розбивати площину на безліч регулярно розташованих рівних фігур, утворюючи різні паркети, орнаменти і мозаїки.

ПЕРЕВІРТЕ СЕБЕ

1.Що таке коливання? Які бувають коливання?

2.Яке коливання називають гармонічним?

3.У яких одиницях визначається амплітуда, період, кутова швидкість, фаза гармонічного коливання?

4.Якими можуть бути амплітуда гармонічного коливання, його період, початкова фаза?

1.Визначте амплітуду, фазу, початкову фазу і кутову швидкість гармонічного коливання, заданого формулою:

а)						; б) у = 0,8sin3t.

120

ПЕРІОДИЧНІ ФУНКЦІЇ І ГАРМОНІЧНІ КОЛИВАННЯ §15

Р о з в ’ я з а н н я. а) Амплітуда дорівнює 6, 2t + – фаза, – початкова фаза, 2 – кутова швидкість.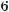

б) 0,8 – амплітуда, 3t – фаза, 0 – початкова фаза, 3 – кутова швидкість.

2. Побудуйте графік функції у = 3cos(2x + 4).

Р о з в ’ я з а н н я. Запишемо функцію у вигляді у = 3cos2(x + 2).

1)Будуємо графік функції у = cosx;

2)стискаємо його до осі у у відношенні 1 : ;

3)отриманий графік переносимо вздовж осі х паралельно на 2 одиниці ліворуч (мал. 83);

у = 2cos x								у = cos(2x + 4)

Мал. 83

4) розтягом від осі х у 3 рази дістанемо, нарешті, потрібний графік (мал. 84).

у = 3cos(2x + 4)

Мал. 84

552. Знайдіть амплітуду гармонічного коливання, заданого формулою:

121