matametika_bevz_standart_1 / matametika_bevz_standart

2 Ðîçäië

Доведемо формулу

Припустимо, що α = х + у і β = х – у. Тоді sin α + sin β = = sin (х + у) + sin (х – у) = sin х соs у + соs х sіn у + sіn х соs у –

–соsх sinу = 2sіnх соsу.

Зрівностей α = х + у і β = х – у знаходимо, що

Тому

Цю тотожність називають формулою суми синусів двох аргументів.

Інші з наведених вище шести формул можна довести простіше, наприклад так:

ПЕРЕВІРТЕ СЕБЕ

1.Сформулюйте формули додавання.

2.Як можна отримати формули подвійних аргументів?

3.Доведіть формули пониження степеня.

4.Які формули називають формулами половинних аргументів?

5.Сформулюйте і доведіть формулу суми синусів двох аргументів.

1. Спростіть вираз:

Р о з в ’ я з а н н я.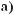

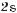
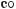
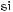
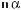
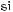
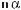
132

НАСЛІДКИ І З ФОРМУЛ ДОДАВАННЯ §17

2. Доведіть тотожність

Р о з в ’ я з а н н я. Перетворимо праву частину тотожності за формулою суми косинусів:

Отже, рівність правильна при будь?яких значеннях α і β. 3. Запишіть у вигляді добутку вираз 1 – 2 соsα.

Р о з в ’ я з а н н я. 1 – 2 соsα =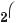

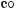
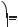
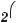
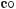
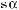
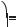
Відповідь.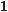

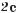
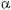
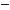
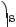
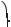
4. Знайдіть найменший невід’ємний корінь рівняння cоs4 х – 1 = sin4 х.

Р о з в ’ я з а н н я. Дане рівняння рівносильне рівнянню

cоs4 х – sin4 х = 1, або (соs2 х + sіn2 х)(соs2 х – sіn2 х) = 1, звідси соs2х = 1, 2х = 0, х = 0.

Спростіть вираз (610–612).

610.

а) 2sinαсоsα;

б) sinхсоsх;

в) 4соsβsinβ;

г) 4sinαсоsαсоs2α.

611.

а) соs2 α – sіn2 α;

б) sin2 х – соs2 х;

612.

в) соs2

– sіn2

;

г) соs2 2α – sіn2 2α.

À

613.

Обчисліть значення виразу:

а) 2sіn15°соs15°;

б) соs2

– sіn2

;

в) sіn

соs

;

133

2 Ðîçäië

г) 1 – 2sіn2 15°; ґ) 2соs2

– 1; д)

Спростіть вираз (614–617).

614.

а) 2sіn2 α + соs2α;

б) 2соs2 α – соs2α;

в) sіn2х – (sіnх + соsх)2;

г) соs2 β (1 – tg2 β).

615.

616.

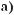
617.
в) (1– tg2α)tg2α;	г) (1– tg2 α) : 2tgα.

Доведіть тотожність (618–620).

618.а) cos2х + sin2 х = cos2 х; б) соs4 х – sin4 х = cos2х;

в) (sinα + соsα)2 = 1 + sin2α; г)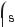

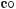
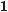
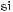
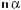
619.

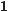
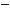
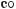
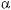
620.	а) 2sin2		+ соsα = 1;
	б) 2соs2 α – соs2α = 1;
	в) (1 + ctg2 α)sin2α = 2 ctgα;
	г) (tgα + ctgα)соs2 α = ctgα – tgα.
621.	Спростіть вираз:
	а) sіn50° + sіn10°;			б) соs50° + соs10°;
	в) sіn50° – sіn10°;			г) соs50° – соs10°.

134

НАСЛІДКИ І З ФОРМУЛ ДОДАВАННЯ §17

Запишіть у вигляді добутку вираз (622–625).

622.

а) sіn5α + sіnα;

б) sіn5β – sіnβ;

в) соsx – соs3x;

г) соsγ + соs7γ.

623.

а) sіn

+ sin

;

б) cos

+ cos

;

в) соsα + соs

;

г) sin

– sinα.

624.

а) tg2β + tgβ;

б) tg3x – tgx;

в) tg(α + β) + tg(α – β);

г) tg

+ tgα.

625.

а) cosα + sіnα;

б) sіn3α – cos2α;

в) sin

– sin

;

г) соs2 α – соs2 β.

Спростіть вираз (626, 627).

626.а) cos(60° + α) + cos(60° – α); б) sin(60° + х) + sin(60° – х).

627.

Á

Доведіть тотожність (628–631).

628.

629.

630.

631.

а) ctgα – tgα = 2ctg2α; б) sin2α – tgα = соs2αtgα.

Запишіть у вигляді добутку вираз (632, 633).

632.

а) 0,5 + sinα;

б) 0,5 – sinx;

в)

г)

ґ)

д)

633.а) cosx + cos2x + cos5x; б) sinα + sin2α + sin3α;

в) sinα + sin2α + sin3α + sin4α; г) cos2x – cos4x – cos6x + cos8x.

634.Доведіть тотожність:

а) sinα sinβ = (cos(α – β) – cos(α + β));

135

2 Ðîçäië

б) sinα cosβ = (sin(α + β) + sin(α – β)).

635. Доведіть, що:

а) sіn35° sіn55° = соs20°; б) cos65° cos25° = соs40°;

636.	Дано: sinα = 0,8; 90° < α < 180°. Знайдіть sin2α і cos2α.
637.	Дано:		270° < α < 360°. Знайдіть sin2α і cos2α.

638.Обчисліть значення sin2α, cos2α, tg2α, якщо tgα = 0,4. Доведіть тотожність (639–642).

639.а) (cos2α + cos6α) tg4α = sin2α + sin6α; б) (cosα + cos5α) tg3α = sinα + sin5α.

640.

641.а) sin2α – tgα = cos2αtgα;

б) sin2α – ctgα = –cos2αctgα; в) ;

г) tg(α + 45°) + tg(α – 45°) = 2tg2α.

642.а) 2sin(45° + α)sin(45° – α) = cos2α; б)

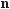
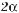
643.Доведіть тотожності Л. Ейлера: а) sin(30° + z) = cosz – sin(30° – z); б) cos(30° + z) = cos(30° – z) – sinz.

644.Покажіть, що всі тригонометричні функції кута α мож?

на представити раціональними виразами через tg .

645.Дано: 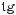Знайдіть sinα, cosα, ctgα.

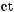
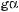
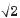
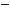
646.Дано: Знайдіть sin2α, cos2α, tg2α.

647.sin3α, cos3α і tg3α виразіть відповідно через sinα, cosα і

tgα.

136

ТРИГОНОМЕТРИЧНІ РІВНЯННЯ І НЕРІВНОСТІ §18

648.Знайдіть моду, медіану і середнє значення вибірки: а) 2, 2, 3, 4, 4, 4, 6, 6, 7, 7, 7, 7, 8; б) 12, 17, 11, 16, 13, 14, 15, 12, 15, 16, 11, 13, 13.

649.Птахоферма збільшила випуск продукції за перший рік на 10 %, а за другий – на 20 %. Як зріс випуск продукції на птахофермі за ці два роки?

650.Розкладіть многочлен на множники:

а) х2 + 5х + 4; б) х2 + 5х + 6; в) х2 – 8х + 15; г) х2 – х – 6.

§18. Тригонометричні рівняння і нерівності

Рівняння називають тригонометричним, якщо його невідомі входять під знаки тригонометричних функцій. Приклади тригонометричних рівнянь:

З а д а ч а. Сторони трикутника дорівнюють 15 см і 8 см. Знайдіть кут між ними, якщо площа трикутника 30 см2.

Р о з в ’ я з а н н я. Площу S трикутника можна визначити за формулою

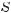
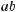
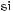
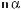
де а, b – його сторони, а

α – кут між ними. Якщо шуканий кут даного трикутника містить х градусів,

то 30 = 15 8 sіnх, звідси sinx = .

Отримали тригонометричне рівняння. Розв’яжемо його. Синус кута

дорівнює 0,5, коли кут має 30° або Мал. 92 150° (мал. 92).

Трикутники з такими кутами існують.

Відповідь. 30° або 150°.

У розглянутому випадку кути не можуть бути від’ємними або більшими за 180°.

Авзагалі рівняння sinx = має безліч розв’язків: 30° + 360° n

і150° + 360° n, де n Z.

Розв’язуючи тригонометричне рівняння, найчастіше знаходять усю множину його розв’язків. I виражають їх здебільшого

137

2 Ðîçäië

не в градусах, а в абстрактних числах. Наприклад, множину

розв’язків рівняння sinx = записують так:

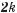
де k Z.

Те, що рівняння sinx = має безліч розв’язків, видно з його

графічного розв’язання: графіки функцій у = sіnх і у = мають безліч спільних точок (мал. 93).

Мал. 93

П р и к л а д и. Розв’яжіть рівняння:

а) 2соsх –

= 0; б) соsх = 0,6.

Р о з в ’ я з а н н я. а) Перетворимо дане рівняння: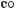

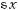
Косинус х дорівнює		коли х =		або х = –		.

Об’єднуючи дві знайдені рівності і враховуючи періодичність функції косинус, можемо записати відповідь:

±+ 2kπ, k Z.

б) Рівняння cоs х = 0,6 можна розв’язати за допомогою калькулятора:

0,6 F arc cos ≈ 0,927.

Отже, маємо множину наближених розв’язків: x ≈ ± 0,927 + 2πn, n Z.

А як знайти множину точних розв’язків такого рівняння? Нехай |а| 1. Арккосинусом числа а називають кут або чис-

ло з проміжку [0; π], косинус якого дорівнює а. Наприклад, аrссоs1 = 0, аrссоs0,5 = , аrссоs0 = , аrссоs(–1) = π.

Множину розв’язків рівняння cоs х = 0,6 можна записати так:

х = ± аrссоs0,6 + 2πn, n Z.

138

ТРИГОНОМЕТРИЧНІ РІВНЯННЯ І НЕРІВНОСТІ §18

Узагалі рівняння cоs х = a при |а| >1 розв’язків не має, а при |а| 1 множина його розв’язків

х = ± аrссоsa + 2πn, n Z.

Подібно до арккосинуса означають арксинус і арктангенс. Нехай |а| 1. Арксинусом числа а називають кут або число

з проміжку

, синус якого дорівнює а. Наприклад,

arсsin1 =

, arсsin

=

, arсsin0 = 0, arсsin(–1) = –

.

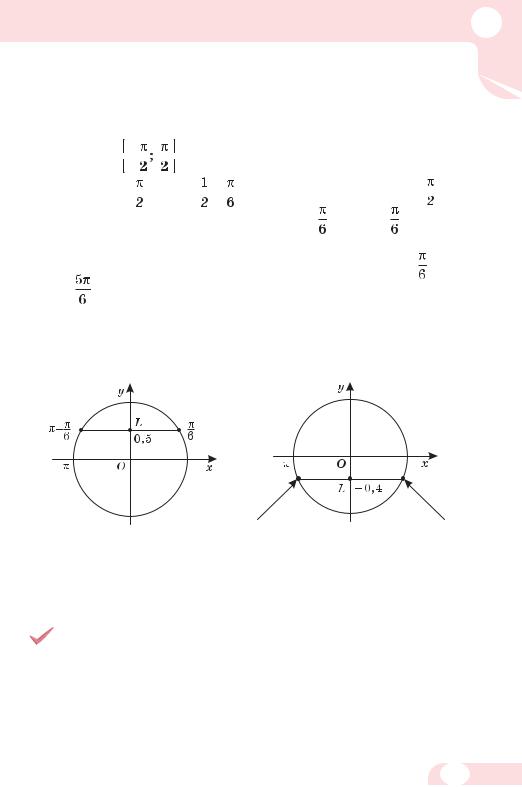
Рівняння sinх = 0,5 має розв’язки х = і х = π – (мал. 94). Оскільки функція sinх періодична з найменшим додатним пе?

ріодом 2π, то дане рівняння має дві серії розв’язків: х = + 2nπ

і х = + 2nπ, n Z.

Розв’яжемо ще рівняння sin х = –0,4.	Два його розв’язки:
х = аrсsіn(–0,4) і х = π – аrсsіn(–0,4) (мал.	95). Усі розв’язки:

х1 = аrсsіn(–0,4) + 2πn і

х2 = π – аrсsіn(–0,4) + 2πn, n Z.

π – аrсsіn(–0,4)	–аrсsіn(–0,4)
Мал. 94	Мал. 95

Узагалі рівняння sinх = а не має розв’язків, якщо |а| > 1; якщо |а| 1, то множина його розв’язків складається з двох серій:

х1 = аrсsіna + 2πn і

х2 = π – аrсsіna + 2πn, n Z.

Зауваження. Дві останні формули можна об’єднати в одну:

х1 = аrсsіna + π 2n, х2 = –аrсsіna + π (2n + 1). Отже, коли множник при π парний чи непарний, то аrсsіn a

береться відповідно з плюсом чи мінусом. Ці випадки об’єднує рівність х = (–1)n аrсsіna + πn, n Z.

Така загальна формула розв’язків рівняння sin х = а, якщо |а| 1.

139

2 Ðîçäië

sin х = 1

sin х = 0

cos х = –1

cos х = 0

а)

б)

в)

г)

Мал. 96

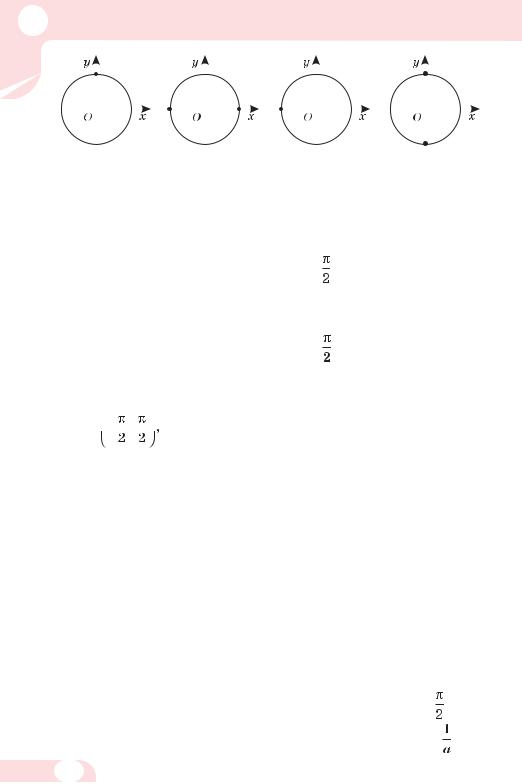
Рівняння sin х = а і cos х = а, якщо а дорівнює 0, 1 або –1, можна розв’язувати і за загальними формулами, але зручніше – уявляючи одиничне коло (мал. 96). Наприклад, рівняння

sinх = 1 має множину розв’язків х = + 2πn;

sinх = 0 має множину розв’язків х = πn;

cosх = –1 має множину розв’язків х = π + 2πn;

cosх = 0 має множину розв’язків х = + πn.

Тут і далі в подібних рівностях n – довільне ціле число. Рівняння tg х = а має розв’язки при будь?якому дійсному а.

Один його розв’язок х = arctgа, де arctgα – кут або число з про? міжку тангенс якого дорівнює а. Оскільки функція tgх

періодична з найменшим додатним періодом π, то множина всіх розв’язків даного рівняння х = аrсtga + πn, n Z.

Формули розв’язків найпростіших тригонометричних рівнянь дано в таблиці.

Рівняння	Формула розв’язків
|а| 1	х = (–1)k аrсsinа + kπ, k Z
sinх = а,
|а| > 1	розв’язків немає
|а| 1	х = ± аrсcosа + 2kπ, k Z
cosх = а,
|а| > 1	розв’язків немає
tgх = а	x = аrсtgа + kπ, k Z

Рівняння ctgх = а при а = 0 має множину розв’язків х = + πn. У всіх інших випадках воно рівносильне рівнянню tgх = .

140

ТРИГОНОМЕТРИЧНІ РІВНЯННЯ І НЕРІВНОСТІ §18

Розв’язуючи складніші тригонометричні рівняння, зводять їх до простіших, як це зазвичай роблять при розв’язуванні алгебраїчних рівнянь. Деякі тригонометричні рівняння зводять до квадратних.

П р и к л а д. Розв’яжіть рівняння 2соs2 х + 3соsх – 2 = 0.

Р о з в ’ я з а н н я. Нехай соs х = у. Рівняння 2у2 + 3у – 2 = 0 має два корені: у = –2 і у = 0,5. Значення косинуса не може дорів?

нювати –2. Отже, соsх = 0,5, звідси х = ±

Відповідь. х = ± + 2πn, де n Z.

А як розв’язати, наприклад, нерів?

ність sinx > ?

Подивимося на одиничне коло (мал. 97). Усі його точки, ординати

яких більші від , лежать на виділеній дузі АА1. Точка А відповідає куту або числу , а точка А1 – куту або числу .

+ 2πn.

Мал. 97

Отже, на проміжку [0; 2π] нерівність

sin x > задовольняє кожне з чисел проміжку Проте

це не вся множина розв’язків. Оскільки при кожному значенні х і цілому n sin(x + 2πn) = sin x, то дану нерівність задовольняють усі числа безлічі проміжків:

Відповідь прийнято записувати так:				де

n Z.

Дану нерівність sin x > можна розв’язати і графічно. Для

цього треба побудувати в одній системі координат графіки функ?

цій y = sinx і 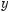(мал. 98). Ті значення х, при яких значення

sin x більші за , утворюють безліч проміжків. Вони і складають

відповідь.

141