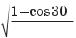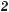matametika_bevz_standart_1 / matametika_bevz_standart
.pdf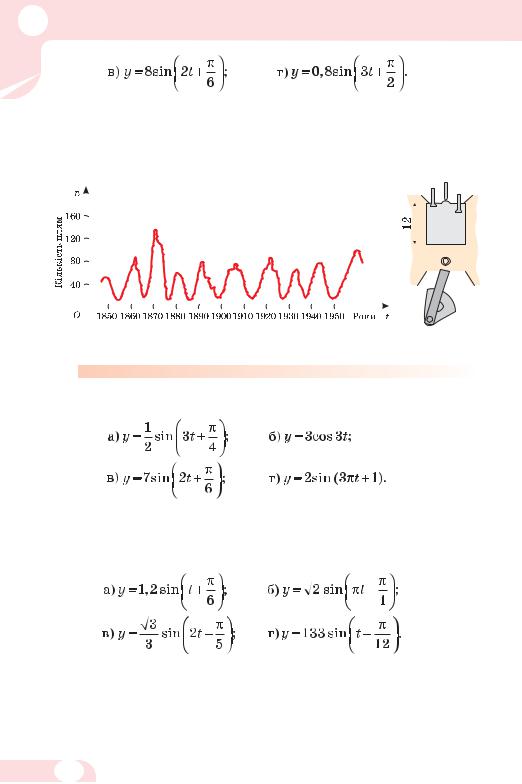
2Ðîçäië
553.На малюнку 85 зображено графік функції, яка виражає залежність кількості сонячних плям від часу. Чи є ця функція періодичною?
554.Хід поршня в циліндрі двигуна дорівнює 12 см (мал. 86). Знайдіть амплітуду його коливання.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мал. 85 |
|
Мал. 86 |
|||
|
|
|||||
À
555.Визначте амплітуду, фазу, початкову фазу і кутову швидкість гармонічного коливання, заданого формулою:
556.Знайдіть період функцій:
a) у = sin6x; б) у = cos0,5x; в) у = 3sin5x; г) у = 0,5cos(x + 1). 557. Знайдіть різницю між найбільшим і найменшим зна-
ченнями функції:
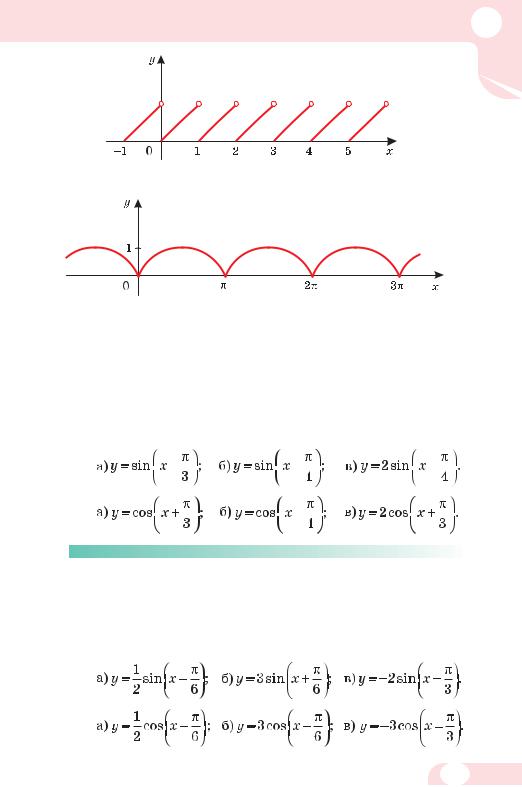
558.На малюнку 87 зображено графік функції «дробова частина числа». Чи періодична ця функція? Якщо так, то який її найменший додатний період? Чи є даний графік гармонікою?
559.На малюнку 88 зображено графік функції у = |sinx|. Чи періодична ця функція? Чи відповідає вона гармонічному коливанню?
122
ПЕРІОДИЧНІ ФУНКЦІЇ І ГАРМОНІЧНІ КОЛИВАННЯ §15
Мал. 87
Мал. 88
Знайдіть період гармонічного коливання (560, 561).
560. |
а) у = sin6x; |
б) у = соs2x; |
в) у = соs0,5x. |
561. |
а) у = соs3x; |
б) у = sin1,5x; |
в) у = sіn4x. |
Побудуйте графік гармонічного коливання (562–565).
562. |
а) у = 2sіnx; |
б) у = –2sіnx; |
в) у = 0,5sіnx. |
||||||||||||||||||||||||
563. |
а) у = 2соsx; |
б) у = –2соsx; |
в) у = 0,5соsx. |
||||||||||||||||||||||||
564. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
565. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Á |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знайдіть період функції (566–568). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
566. |
а) у = 7sin2x; |
б) у = 2соs6x; |
в) у = 0,2sin(x + π). |
||||||||||||||||||||||||
567. |
а) у = 5sin0,1x; |
б) у = соs(2x +3); |
в) у = 6sіn(2 + 3x). |
||||||||||||||||||||||||
568. |
а) у = tg2x; |
б) у = 3tg0,25x; |
в) у = ctg(3x – 0,5π). |
||||||||||||||||||||||||
Побудуйте графік функції (569–573).
569.
570.
123

2Ðîçäië
571.


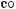
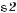
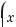
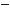
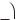
572.


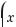
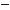

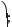
573*.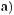
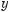


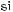



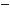
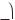

574.Побудуйте графік періодичної функції з періодом T = 2,
якщо на проміжку [–1; 1] її можна задати формулою: а) y = x2; б) y = x2 – 1.
575.Побудуйте графік періодичної функції з періодом T = 4, якщо на проміжку [–2; 2] її можна задати формулою:
а) y = |x|; б) y = 1 – |x|.
576. Дивлячись на графіки гармонічних коливань (мал. 89), напишіть відповідні їм функції.
Мал. 89
577. Електричний струм, який живить міську освітлювальну мережу, є змінним струмом. Його сила I постійно змінюється, здійснюючи гармонічне коливання
де I0 – максимальне значення сили струму; Т – період коливання; ϕ – початкова фаза.
В які моменти часу сила струму досягає мінімального або максимального значення і коли його значення дорівнює нулю?
124
ФОРМУЛИ ДОДАВАННЯ §16
Спростіть вираз (578, 579).
578.а) (1 – cos2 α + sin2 α)ctg2 α; б) 1 – sіnβсоsβtgβ + sin2 α.
579.
580. Чи є число 143 членом арифметичної прогресії 3, 8, 13, ...? Якщо так, то знайдіть номер цього члена прогресії.
§ 16. Формули додавання
Теорема. Які б не були кути або числа  і
і  , завжди
, завжди
соs( + ) = соs соs + sіn |
sin . |
Д о в е д е н н я. Нехай α і β – довільні |
|
кути. На одиничному колі їм відпо- |
|
відають точки А (соs α; sіn α) і В (соs β; |
|
sinβ) (мал. 90). Виразимо квадрат від- |
|
стані між точками А і В двома способа- |
|
ми. Якщо АОВ = α – β, де 0 < α – β < π, |
|
то за теоремою косинусів |
|
АВ2 = ОА2 + ОВ2 – 2 ОА × |
|
× ОВ соs(α – β) = 2 – 2соs(α – β). |
|
Згідно з теоремою про квадрат |
|
відстані між двома точками |
|
АВ2 = (соsα – соsβ)2 + (sіnα – sinβ)2 = |
Мал. 90 |
= соs2 α – 2 соs αсоs β + соs2 β + sіn2 α – 2 sіn αsin β + sin2 β = 2 –
– 2(соsαсоsβ + sіnαsinβ).
Отже, 2 – 2 соs (α – β) = 2 – 2(соs α соs β + sіn α sin β), звідси соs (α – β) = соsαсоsβ + sіnαsinβ.
Ми розглянули випадок, коли АОВ = α – β, де 0 < α – β < π. В інших випадках кут АОВ може дорівнювати α – β + 2πn або β – α + 2πn, де n N (мал. 91). Косинус кожного з таких кутів дорівнює соs (α – β). Тому теорема, що доводиться, правильна для будь?яких кутів α і β, а отже, і для довільних дійсних чисел α і β.
На основі доведеної теореми і формул зведення можна вивести подібні формули для перетворення виразів соs(α + β) і sіn(α ± β).
соs (α + β) = соs (α – (–β)) = соs α соs (–β) + sin α sіn (–β) = = соs α соsβ – sіnαsіnβ.
125

2 Ðîçäië
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
б) |
|||
Мал. 91
sіn(α – β) = sіn(α + (–β)) = sіnα соs(–β) + соsα sіn(–β) = = sіnα соsβ – соsα sіnβ.
Доведемо ще формули для перетворення виразів tg(α ± β).
Отже, маємо 6 формул:
sin(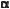
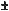
 )
)  sіn
sіn 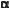 соs
соs 
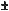 соs
соs 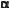 sіn
sіn  , соs(
, соs(
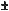
 )
)  соs
соs  соs
соs 
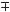 sіn
sіn 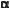 sіn
sіn  ,
,
Це – формули додавання. Чотири перші з них правильні для будь?яких кутів або чисел α і β, дві останні – для будь?яких допустимих значень α і β (коли всі тангенси у формулі мають значення).
126

ФОРМУЛИ ДОДАВАННЯ §16
 ПЕРЕВІРТЕ СЕБЕ
ПЕРЕВІРТЕ СЕБЕ
1.Які тригонометричні рівності називають формулами додавання?
2.Як визначається косинус різниці двох кутів?
3.Чи одне й те саме означає косинус суми і сума косинусів?
4.Як визначається косинус суми двох кутів?
5.Як визначається тангенс суми (різниці) двох кутів?
1. За допомогою формул додавання перетворіть вираз:
 Р о з в ’ я з а н н я.
Р о з в ’ я з а н н я.
2. Обчисліть значення sіn75°.
 Р о з в ’ я з а н н я. sіn75° = sіn(30° + 45°) = sіn30° cos45° +
Р о з в ’ я з а н н я. sіn75° = sіn(30° + 45°) = sіn30° cos45° +
+ cos30° sin45° = 








Відповідь. 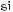




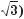

3. Обчисліть значення виразу cos35°cos25° – sin35°sin25°.  Р о з в ’ я з а н н я. cos35°cos25° – sin35°sin25° = cos(35° + 25°) =
Р о з в ’ я з а н н я. cos35°cos25° – sin35°sin25° = cos(35° + 25°) =
=cos60° = 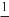 .
.
581.Які вирази мають бути в порожніх клітинках таблиці?
α + β α + x α – x |
c + 1 |
c – 2 |
sin
cos
tg
127

2Ðîçäië
582.Спростіть вираз:
|
|
а) sіnα соsβ + соsα sіnβ; |
б) sіnα соsβ – соsα sіnβ; |
||||
À |
|
в) соsα соs2 – sіnα sіn2; |
г) соsхсоsy + sіnxsіny. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Спростіть вираз (583, 584). |
|
|
|
|
|
||
583. |
а) sіnα соsх + соsα sіnх; |
б) соsβ sіnα – соsα sіnβ; |
|||||
|
|
в) sіnα sіnβ – соsα соsβ; |
г) sіnα sіn |
|
+ соsα соs |
|
. |
|
|
|
|
||||
584. |
а) sіn(α + β) – sіnα соsβ; |
б) sіnα sіnβ + соs(α + β). |
|||||
|
|
в) sіn(α + β) – sіn(α – β); |
г) соs(α – β) + соs(α + β). |
||||
Обчисліть значення виразу (585–587).
585.a) cos57°cos27° + sin57° sin27°; б) sin11°соs19° + cos11°sin19°; в) cos51°sin21° – cos21°sin51°; г) sin12°cos18° + cos12°sin18°.
586.a) cos58°cos32° – sin58°sin32°; б) sin65°соs55° + cos65°sin55°; в) sin64°sin19° + cos64°cos19°; г) cos10°cos20° – sin20°sin10°.
587.a) (tg36° + tg24°) : (1 – tg36°tg24°); б) (tg70° – tg40°) : (1 + tg70°tg40°).
Доведіть тотожність (588–590).
588.а) sіn(α + β) + sіn(α – β) = 2sіnα cosβ; б) cos(α – β) – cos(α + β) = 2sіnα cosβ.
589.

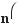



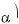





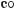
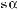

590.а) 

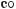
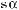

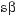
 б)
б) 

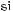

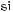
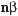

591.Обчисліть значення соs75°, tg75°, ctg75°. Обчисліть значення виразу (592–596).
592. |
а) sіn15°; |
б) соs15°; |
в) tg15°; |
г) ctg15°. |
593. |
а) sіn105°; |
б) соs105°; |
в) tg105°; |
г) ctg105°. |
128







 ,
,
 cos
cos  – sіn
– sіn



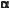

 (1 – соs2
(1 – соs2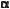 )
)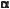

 (1 + соs2
(1 + соs2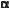 ).
).