matametika_bevz_standart_1 / matametika_bevz_standart

1 Ðîçäië

Властивості коренів n9го степеня:

1)	; 2)				; 3)	;
4)	;	5)				.

Степені з дробовими показниками: . Властивості. Якщо r і s – числа раціональні, то:

1)	; 2)					; 3)				;
	4)	; 5)								.

Степенева функція y = xα , x (0; +∞), α Q.

Властивості: функція монотонна, ні парна, ні непарна. При α > 0 функція зростаюча, при α < 0 – спадна. Графік функції проходить через точку М (1; 1).

y = xα, α > 0

M

y = xα, α < 0

M

Рівняння називають ірраціональним, якщо воно містить змінну під знаком кореня або в основі степеня з дробовим показником. Найзагальніший спосіб розв’язування ірраціональних рівнянь – піднесення обох його частин до однакових степенів з наступним відкиданням сторонніх розв’язків. Багато ірраціональних рівнянь зручно розв’язувати за допомогою заміни змінної.

82

Розумова праця на уроках математики – пробний камінь мислення.

В. О. Сухомлинський

§10. Синус, косинус, тангенс і котангенс кута

Ужитті ми часто стикаємося з процесами, які відбуваються

зпевною періодичністю. Скажімо, на зміну зимі приходить весна, на зміну весні – літо, на зміну літу – осінь, на зміну осені – зима, знову весна, і все повторюється з року в рік. Так само змінюються ранок, день, вечір і ніч. Періодичні процеси відбуваються в багатьох механізмах (рух поршня, маятника) і в живих організмах (пульсація серця, дихання).

	Мати справу з процесами, які періо-
	дично повторюються, доводиться ба-
	гатьом фахівцям. Моделювати такі
	процеси найзручніше за допомогою си-
	нуса, косинуса, тангенса і котангенса.
	Дещо про ці функції ви вже знаєте з
	уроків геометрії.
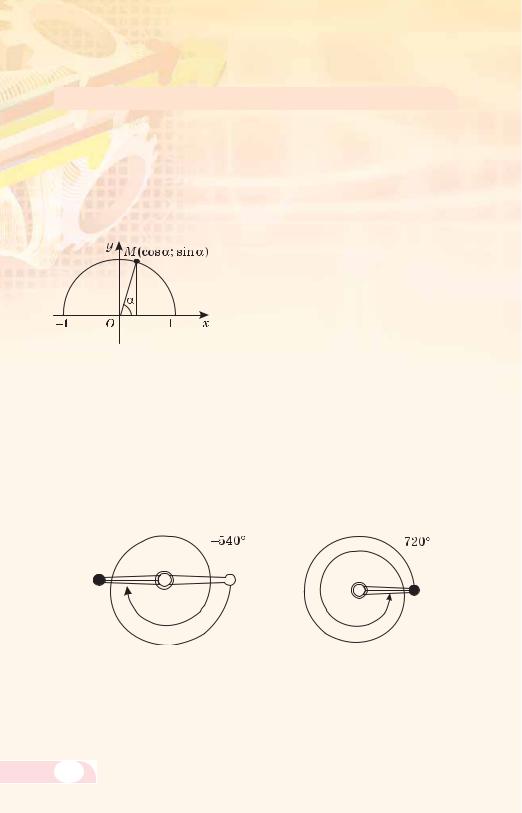
	Синус (косинус) гострого або тупого
Мал. 48	кута α – це ордината (абсциса) точки
одиничного півкола, яка відповідає куту α (мал. 48).
Зверніть увагу: в геометрії розглядають sinα, соsα, tgα, ctg α
за умови, що α – кут трикутника або опуклого многокутника,
тобто коли 0° < α < 180°. Досліджуючи ж періодичні процеси,
під α розуміють кут повороту (обертання). А він може бути і як
завгодно великим, і від’ємним. Повороти в напрямі руху го-
динникової стрілки домовилися вважати від’ємними, а в про-
тилежному напрямі – додатними. Наприклад, повернути корбу
на –540°, на 720° – це означає повернути її, як показано на
малюнках 49, а і б.

а)

б)

Мал. 49

Одному, двом, трьом, ..., n обертам відповідають кути 360°, 720°, 1080°, ..., 360° n.

Уведемо поняття синуса, косинуса, тангенса і котангенса будь?якого кута. Зробимо це за допомогою одиничного кола.

84

СИНУС, КОСИНУС, ТАНГЕНС І КОТАНГЕНС КУТА §10

Мал. 50

Мал. 51

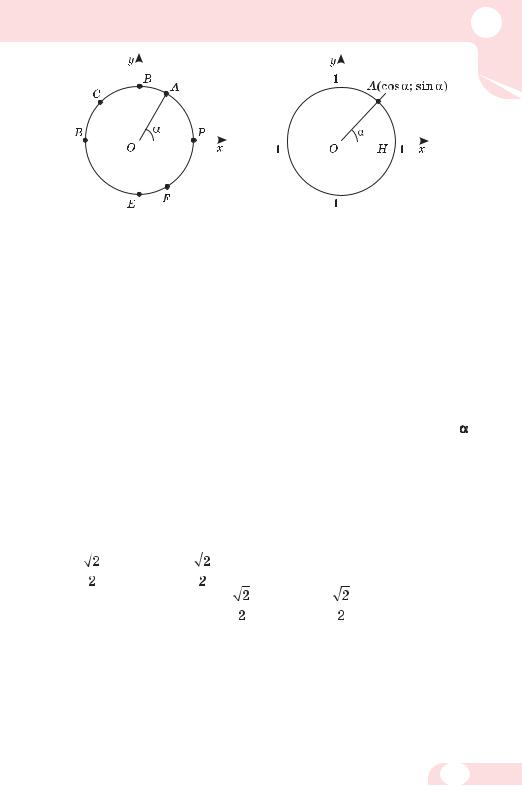
Якщо центром кола є початок координат, а його радіус дорівнює 1, то таке коло називають одиничним колом.

Нехай на координатній площині дано одиничне коло і його початковий радіус ОР (мал. 50). Кажуть, що точка А одиничного кола відповідає куту α, якщо РОА = α. Зображені на малюнку 50 точки Р, А, В, С, D, Е, F відповідають кутам 0°, 60°, 90°, 135°, 180°, 270°, 300° (у межах від 0° до 360°).

Синусом кута називається ордината точки одиничного кола, яка відповідає куту .

Косинусом кута називається абсциса точки одиничного кола, яка відповідає куту (мал. 51).

Тангенсом кута називається відношення синуса кута до його косинуса.

Котангенсом кута називається відношення косинуса кута до його синуса.

Синус, косинус, тангенс і котангенс кута α позначають відповідно символами sіnα, соsα, tgα, сtgα.

П р и к л а д и.

1. Куту 135° на одиничному колі відповідає точка С із абсци?

сою

і ординатою

(мал. 50). Тому

соs135° =

, sin135° =

,

tg135° = –1, ctg135° = –1.

2. Куту –90° на одиничному колі відповідає точка Е (0; –1).

Тому	соs(–90°) = 0, sіn (–90°) = –1,
	ctg(–90°) = 0, tg(–90°) не існує.

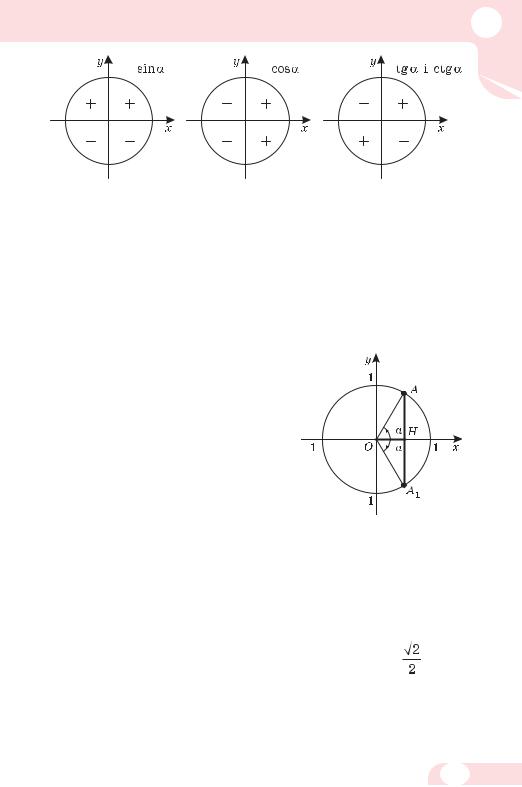
Тангенс кута α має значення (тобто існує) тоді і тільки тоді, коли соsα 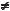0, адже ділити на 0 не можна. Котангенс кута α має значення тільки за умови, що sinα 0.

85

2 Ðîçäië

Значення sіn α, соs α, tg α, ctg α деяких кутів α наведено в таблиці.

	0°	30°	45°	60°	90°
sin	0				1
соs	1				0
tg	0		1		–
сtg	–		1		0

Наближені значення тригонометричних функцій можна знаходити за допомогою мікрокалькулятора або спеціальних таблиць (див. додатки на с. 261).

Кожному значенню кута α відповідає єдине значення sіn α (див. мал. 51). Значення sіn α залежить від значення α. Тому sinα – функція від α. Функціями від α є також соsα, tgα, ctgα. Детальніше ми розглянемо їх далі, а тут звернемо увагу тільки на найважливіші властивості цих функцій.

Нагадаємо, що sin α – це ордината

							точки А одиничного кола, яка від-
							повідає куту α (мал. 52). Якщо АН –
							перпендикуляр, опущений з точки А
							на вісь х, то довжина відрізка АН –
							синус кута α, а ОН – косинус кута α.
							Якщо точка А знаходиться у І або II
							координатній чверті, то sin α = АН;
							якщо точка А – у III або IV чверті, то
							sin α = –АН. Кажуть, що у І і II чвер-
							тях синус кута α додатний, а в III і IV
		Мал. 52					чвертях – від’ємний.
							Знаки тригонометричних функцій

кутів різних координатних чвертей показано на малюнку 53. Якщо кут α збільшується від 0° до 90°, то значення sin α

збільшується від 0 до 1. Якщо α збільшується від 90° до 180°, то значення sinα зменшується від 1 до 0. Якщо α збільшується від 180° до 270°, то значення sinα зменшується від 0 до –1. Якщо α збільшується від 270° до 360°, то значення sin α збільшується від –1 до 0. Отже, для будь?якого значення α:

–1 sinα 1 і –1 соsα 1.

Якщо кут α продовжувати збільшувати, то всі ці властивості повторяться, тобто завжди

sinα = sin(α + 360°) = sin(α – 360°) = sin(α + 720°) = ...

86

СИНУС, КОСИНУС, ТАНГЕНС І КОТАНГЕНС КУТА §10

Мал. 53

Узагалі, яким би не був кут α і ціле число n, то:

sin(α + 360° n) = sinα,	соs(α + 360° n) = соsα,
tg(α + 360° n) = tgα,	ctg(α + 360° n) = ctgα.

Ці співвідношення дають можливість звести знаходження значень синуса, косинуса, тангенса й котангенса будь?якого кута до знаходження їх значень для невід’ємного кута, меншого від 360°. Нехай, наприклад, треба обчислити соs 1860°. Поділивши 1860 на 360, дістанемо частку 5 і остачу 60. Отже,

соs1860° = соs(360° 5 + 60°) = соs60° = 0,5. Як видно з малюнка 54, косинуси

кутів 60° і –60° однакові, оскільки точки А і А1 симетричні відносно

осі х. Тому соs (–60°) = соs 60°. І взагалі, косинуси кутів α і –α завжди однакові. Тому, який би не був кут α, завжди соs(–α) = соsα.

Відрізки АН і А1Н мають одна-
кові довжини, але розміщені по різні
боки від осі х, тому їхні знаки різні.
Отже, sіn (–α) = –sіn α для кожного
значення α.
Таким чином, правильні тотож-			Мал. 54
ності:
соs(–α) = соsα,	sіn (–α) = –sіn α,
tg(–α) = –tgα,	ctg(–α) = –ctgα.

Користуючися ними, можна порівняно легко обчислювати значення тригонометричних функцій від’ємних кутів.

П р и к л а д и :

1. sіn (–30°) = –sіn 30° = –0,5;
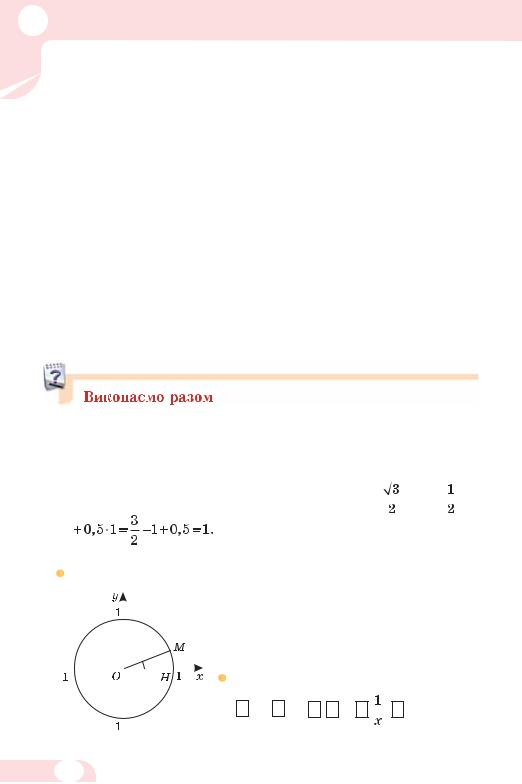
2. соs(–405°) = соs405° = соs(45° + 360°) = соs45° =	.

Синус, косинус, тангенс і котангенс разом називають тригонометричними функціями. Ця назва походить від назви давньої науки тригонометрії. Раніше тригонометрію найчастіше використовували для розв’язування трикутників, а з їх допомогою – розв’язування багатьох геометричних і геодезичних задач.

87

2Ðîçäië

У XX ст. такі задачі навчилися розв’язувати іншими способами й засобами, навіть простіше й точніше, тому тепер тригонометрія втратила попередню цінність і її не відносять до сучасних наук. Але поняття синус, косинус, тангенс і котангенс у різних науках продовжують відігравати важливу роль. Особливо, коли йдеться про різні обертальні рухи, періодичні процеси і явища.

ПЕРЕВІРТЕ СЕБЕ

1.Що таке синус кута α? Якого значення він може набувати?

2.Яких значень у виразі sin α може набувати α?

3.Сформулюйте означення косинуса кута.

4.За яких умов косинус кута додатний? А коли – від’ємний?

5.Що таке тангенс кута? А котангенс?

6.При яких значеннях α його тангенс не існує? А котангенс?

7.Як змінюється синус кута, якщо кут збільшується: а) від 0° до 90°; б) від 90° до 180°?

8.Як змінюється косинус кута, якщо кут збільшується: а) від 0° до 90°; б) від 90° до 180°?

9.Як змінюється тангенс кута, якщо кут збільшується: а) від 0° до 90°; б) від 90° до 180°?

1. Обчисліть:

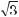
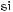
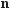
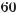
– 2sіn90° соs60° + 0,5tg45°.

Р о з в ’ я з а н н я. Відповідні значення синуса й косинуса знаходимо в таблиці (див. с. 86). Маємо:

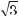
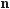
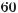
– 2sіn 90° соs 60° + 0,5tg 45° =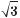

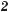
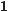
		2. Що більше: sіn 20° чи соs20°?
		Р о з в ’ я з а н н я. Якщо МОН = 20°, то								ОМН = 70°
							(мал. 55). Оскільки в трикутнику проти
							більшого кута лежить більша сторона,
							то ОН > МН. Отже, соs20° > sіn20°.
							3. Користуючися мікрокалькулято-
							ром, обчисліть ctg42°13′.
							Р о з в ’ я з а н н я.
							13 ÷ 60 + 42 = F tg F				= 1,1022016.
							Відповідь. ctg42°13′ ≈ 1,1022.
		Мал. 55

88

СИНУС, КОСИНУС, ТАНГЕНС І КОТАНГЕНС КУТА §10

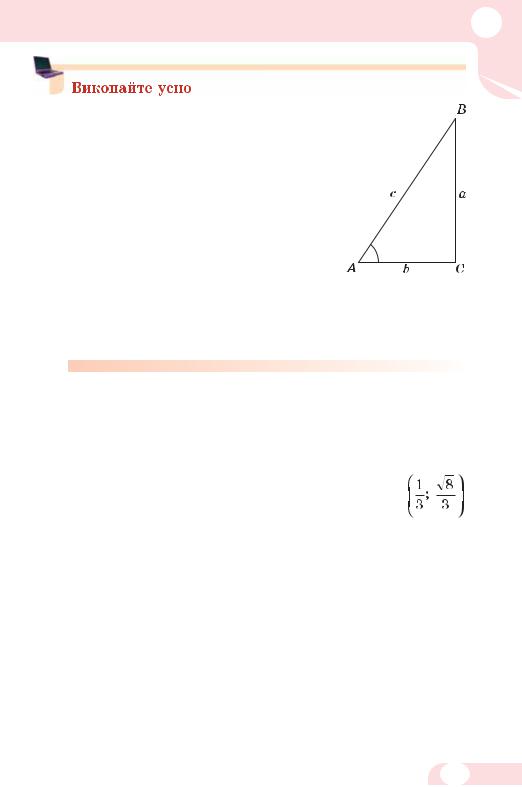
384. Дивлячися на прямокутний трикутник АВС (мал. 56), укажіть значення синуса, косинуса, тангенса й котангенса кутів А, В і С.

385.Чи може абсциса або ордината точки одиничного кола дорівнювати 2?

386.Чи може синус або косинус кута дорівнювати 2? А –2?

387.Чи може синус кута, меншого від 180°, бути числом від’ємним? А косинус?

388.Тангенс якого кута дорівнює 1?

А–1?

389.	Укажіть значення синуса, косинуса,	Мал. 56
тангенса й котангенса прямого кута і кута 45°.
390.	Якій чверті належить кут: 100°, 150°, 200°, 250°, 300°,
350°?

À

391.На скільки градусів повертається годинна стрілка протягом півдоби? А хвилинна стрілка?

392.Накресліть одиничне коло і позначте на ньому точки, які відповідають кутам: 30°, 90°, 120°, 180°, 270°, 360°, –30°, –300°.

393.Обчисліть значення кожної тригонометричної функції кутів, заданих у № 392.

394.Куту α на одиничному колі відповідає точка М .

Укажіть значення sinα, соsα, tgα, ctgα.

395.Куту β на одиничному колі відповідає точка з абсцисою 0,6. Укажіть значення sinβ, соsβ, tgβ, ctgβ.

396.Як змінюється sin α і соs α, якщо α збільшується від 0° до 360°?

397.Щo більше:

а) sin20°	чи	sin50°;	б) соs40°	чи соs10°;
в) sin20°	чи	sin160°;	г) соs10°	чи соs100°?
398. Обчисліть:
а) sin30° + соs30°;			б) соs60° – sіn 45°;
в) sin45° соs45°;			г) 2sin60° соs60°.

399.Знайдіть значення синуса, косинуса, тангенса, котангенса кута правильного: а) трикутника; б) чотирикутника; в) шестикутника.

400.Замість зірочки поставте знак > або <:

а) соs5° * соs7°; б) sіn82° * sіn79°; в) sіn178° * sіn108°;

89

2 Ðîçäië

г) соs113° * соs115°; ґ) tg29° * tg32°; д) tg97° * tg107°.

401.Обчисліть значення виразу:

а) sіn45° – соs60° соs90° + sіn120°; б) sіn30° соs150° – соs60° tg120°.

402.Визначте знак добутку:

а) sіn120° соs155° tg85°;	б) sіn320° соs55° ctg185°;
в) ctg124° соs115° tg35°;	г) ctg125° соs77° tg305°.

403. Обчисліть значення тригонометричних функцій за допомогою таблиць і перевірте результат, використовуючи калькулятор:

а) sіn12°, sіn33°, sіn72°, sіn50°; б) соs12°, соs33°, соs72°, соs50°; в) tg12°, tg33°, tg72°, tg50°;

г) ctg12°, ctg33°, ctg72°, ctg50°.

Á

Визначте знак добутку (404, 405).

404.а) соs30° sіn715° соs125° tg35°; б) sіn137° соs150° tg22° соs735°.

405.a) tg143° sіn565° tg87° соs126°; б) соs932° sіn132° соs135° tg92°.

406.Обчисліть значення виразу:

а) sіn30° соs60° – соs2120° + sіn135° соs90°;

б) tg30° tg60° – tg2135° + соs150°. Знайдіть значення виразів (407, 408).

407.а) соsα + 3sіnα, якщо α = 45°;

б) sіnβ + sіn2β + sіn3β, якщо β = 60°.

408.a) sіnγ + 2соsγ + 3tgγ, якщо γ = 30°;

б) sіnα + соs(α – β), якщо α = 90° і β = 30°.

409.Яке найбільше і найменше значення може мати вираз:

а) 3sіnх; б) – соsх; в) 1 + sіnх; г) sіnх – 1?

410. Чи може синус або косинус кута дорівнювати:

411.	а)	б)		в)			г)
	Користуючися мікрокалькулятором, обчисліть:
	а) sіn17°;			б) cos35,7°;			в) sin110°;
	г) tg39,8°;			ґ) 3соs25°;			д) 10tg38°;
412.	e) 2 + соs49°;			є) 3 + sіn47°.
	Обчисліть:
413.	а) ctg37,8°;			б) 2,7ctg63,7°;			в) 2 : sіn36,3°.
	Користуючися таблицею (додатки на с. 261), знайдіть:
	a) 1 + sіn25°;			б) sіn20° – соs70°;			в) 2sіn15°соs15°.
414.	Знайдіть міру гострого кута х, якщо:
	а) sinx = 0,5;			б) 2 cosx = .

90

ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ ЧИСЛОВОГО АРГУМЕНТУ §11

415. Знайдіть sіnα і соsα, якщо: а) tgα = 1; б) tgα = –1.

416.Знайдіть sіnα і tgα, якщо соsα = 0,5 (кут α гострий).

417.Знайдіть, користуючись одиничним колом:

sіn0°, sіn90°, соs90°, sіn180°, соs180°, sіn270°, соs270°.

418.Що більше:

а) sіn10° чи соs10°; б) соs45° чи sіn45°?

419.Який з кутів більший – α чи β, якщо:

а) sіnα = 0,75, sіnβ = 0,93; б) соsα = 0,5, соsβ = 0,6?

420.Яких значень при різних значеннях α може набувати

вираз:

sіn2 α, 1 – sіn2 α, sіn2α, 2sіnα?

421.Яких значень може набувати вираз:

tgα, tg2 α, tg2α, 2tgα, 1 + tgα?

422.Накресліть на міліметровому папері чверть кола раді-

уса 10 см, поділіть його на 30 рівних частин і складіть таблицю наближених значень синуса й косинуса кутів 3°, 6°, ... , 90°.

423.Знайдіть довжину кола й площу круга, радіус яких дорівнює:

а) 2 м; б) 12 см; в) 2,5 дм.

424.З а д а ч а С у н ь ? Ц з и . Знайдіть число, яке від ділення на 3 має в остачі 2, а від ділення на 5 має в остачі 3, нарешті від ділення на 7 – остача 2.

425.Побудуйте графік функції:

а) у = 4х–2; б) у = 4х–2 + 1; в) у = 6х–1; г) у = 6х–1 – 2.

§11. Тригонометричні функції числового аргументу

Досі ми розглядали тригонометричні функції кутів. При цьому вирази х + sіnх, соsх2 не мали змісту. Оскільки не можна до градусної міри кута додавати число. Не має змісту й квадрат міри кута. А розв’язування багатьох задач приводить до аналізу подібних виразів. Тому математики часто мають справу з виразами sіnα, соsα, tgα, ctgα, де α – не міра кута, а абстрактне число. Що ж розуміють під синусом, косинусом, тангенсом і котангенсом дійсного числа?

Спочатку згадаємо дещо про вимірювання кутів. Кути можна вимірювати градусами та їх меншими частками: мінутами і секундами. А ще можна вимірювати кути радіанами.

91