
- •1.2. Типичная функциональная схема и основные преобразования
- •Цифровой выход, mi Цифровой вход, mi
- •Цифровые и аналоговые критерии производительности
- •Спектральная плотность энергии
- •Различают два вида дискретных сигналов:
- •Функции приемника
- •Пример.
- •Пример.
- •Причины памяти реальных дискретных каналов.
- •Модель канала с памятью
- •Здесь p(ci/ci-1) – переходные вероятности состояний канала.
- •Пример.
- •Отношение — это естественный критерий качества
- •Импульсы Найквиста
- •Методы цифровой полосовой модуляции
- •Фазовая манипуляция
- •Амплитудная манипуляция
- •Амплитудно-фазовая манипуляция
- •Цифровой согласованный фильтр
- •Компромисс между полосой пропускания и мощностью
- •Абонентская линия isdn (цсис)
- •Технология xDsl
- •Расширенный код Голея
- •Коды бхч
- •Система с иос-ож.
- •Система с рос-ож
- •Система с рос-нп
- •Коды Лемпеля-Зива (zip)
- •Примеры кодирования источника
- •Аудиосжатие
- •Типичные значения параметров для трех классов аудиосигналов
- •Адаптивная дифференциальная импульсно-кодовая модуляция
- •Уровни I, II и III стандарта мреg
- •Дополнительная литература:
Модель канала с памятью
Пусть состояния канала различаются по вероятности ошибки в символе. Такой канал задается совокупностью переходных вероятностей вида
где
С – конечное множество состояний канала.
Это условная вероятность приема символа
bi
и перехода дискретного канала в состояние
ci
в i-й
момент времени, если передавался символ
ai
, а в предыдущий момент времени (i-1)
канал находился в состоянии сi-1
.
Если
предположить, что состояние канала в
i-й
момент времени сi
статистически не зависит от входных и
выходных символов, то при заданном
символе входного алфавита в i-й момент
времени ai
и известном состоянии канала в предыдущий
(i-1)-й момент сi-1
можно записать
Здесь p(ci/ci-1) – переходные вероятности состояний канала.
В каждом состоянии ci ошибки возникают независимо друг от друга с постоянной вероятностью.
Последовательность состояний ДК с памятью является простой цепью Маркова. Простая цепь Маркова – это случайная последовательность состояний (или символов и т.д.), в которой вероятность перехода в состояние ci полностью определяется состоянием ci-1 . Для описания простой цепи Маркова надо задать переходные вероятности вида P(ci/ci-1) . Переходные вероятности записываются в виде квадратной матрицы. Порядок матрицы переходных вероятностей равен числу состояний дискретного канала.
Модель двоичного симметричного канала с памятью, имеющего К состояний, задается матрицей переходных вероятностей
и
вероятностями ошибки в каждом состоянии
канала

Элементы
матрицы переходных вероятностей
удовлетворяют условию
Пример.
Канал может находиться в трех состояниях. Последовательность состояний является простой цепью Маркова. Какое число переходных вероятностей необходимо знать для задания модели канала? - 9.
Средняя
вероятность ошибочного приема двоичного
символа
в канале с К состояниями определяется
по формуле
Рi – финальные, то есть безусловные вероятности состояний канала в произвольный момент времени i. Финальные вероятности определяются из системы уравнений:
Тогда
средняя вероятность ошибки в двоичном
символе для такого канала равна Pe=P1
1+P2
2+…+Pk
k.
Средняя вероятность безошибочного приема двоичного символа равна
Q=1-Pe.
Модели дискретных каналов
Несоответствие принятого элемента сигнала данных переданному называется ошибкой.
С. целью аналитического моделирования систем ПДС проведены многочисленные исследования закономерности потоков ошибок и предложен ряд математических моделей дискретных каналов [5]. При этом к моделям источника ошибок предъявляются следующие требования: удобство аналитического моделирования систем ПДС, обеспечивающее достаточное соответствие модели систем и реальным объектам; простота оценки параметров модели в результате измерений.
Модель дискретных каналов может строиться двумя способами, Если при первом способе применяются существующие математическиe модели случайных процессов и экспериментально оценивается достаточно большое число их параметров, то при втором используются аппроксимационные способы представления потока ошибок. В случае, когда ошибки в каналах появляются независимо с вероятностью рош, вероятность появления в n-элементной комбинации t ошибок P(t,n) определяется биномиальным распределением!
р
(t,n)=
При этом вероятность приема неискаженной комбинации (t=0),
Р(0,n)= ,
,
а вероятность появления хотя бы одной ошибки (рис. 1.6)
 .
.
Вероятность появления т и более ошибок
![]()
Для
большинства каналов данная модель
приводит к недопустимым
погрешностям. В соответствии с моделью
Гильберта, учитывающей
группирование ошибок, канал может
находиться в одном
из двух состояний — «хорошем», когда
ошибки невозможны, и
«плохом»,
когда возникают независимые ошибки с
вероятностью
 . Канал
задается матрицей переходных вероятностей
. Канал
задается матрицей переходных вероятностей

(1.21)
и
вероятностью
 .
Вероятность ошибки в канале
.
Вероятность ошибки в канале
pош
=
 p10/(p01+p10).
(1.22)
p10/(p01+p10).
(1.22)
Вероятность возникновения пакета ошибок с данного элемента
pп == p01p10/(p01+p10).
Другой распространенной моделью является модель В. Беннета и Ф. Фройлиха, которая задается тремя параметрами:
вероятностью появления пакета рп, равной отношению чиcла пакетов к общему числу переданных бит; пакеты независимы; ; распределением вероятностей пакетов рп(l) различной длины l;
вероятностью ошибки в пакете рош.п.
Простейшей моделью, учитывающей группирование ошибок в пакеты, является модель Бергера — Мандельброта.
Обобщением модели Беннета-Фройлиха является модель Попова — Турина, которая предполагает существование в канале независимо возникающих цепочек пакетов ошибок. Распределение длин цепочек полагается геометрическим. Внутри цепочек независимо появляются пакеты ошибок, длины которых распределены по полигеометрическому закону. Внутри пакетов задается условная вероятность появления ошибок.
Задача
1.20.
Определить вероятность Р( 1,
n)
ошибочного
приема для каналов
с независимыми ошибками кодовой
последовательности длиной n=9
для
рош=1•10-3
и 1•10-5.
1,
n)
ошибочного
приема для каналов
с независимыми ошибками кодовой
последовательности длиной n=9
для
рош=1•10-3
и 1•10-5.
Решение.
Вероятность Р( 1,
n)
= 1—(1—Рош)n
1,
n)
= 1—(1—Рош)n
 npош
=
9•10-3
и 9•10-5
npош
=
9•10-3
и 9•10-5
Задача 1.21. Определить для тех же условий вероятности приема неискаженной комбинации P(Q, п), а также вероятности появления т=2, ..., 5 и более.
Рассмотрим двухпараметрическую модель дискретного канала Л. П. Пуртова [49, 71]. Вероятность появления искажений кодовой комбинации длиной п (см. рис. 1.6)
 при
пр
<<
1.
при
пр
<<
1.
При
а 0
имеем случай независимого появления
ошибок, а при а
0
имеем случай независимого появления
ошибок, а при а 1
— появления групповых ошибок (при а= 1
вероятность искажений
комбинации не зависит от n,
так как в каждой ошибочной комбинации
все элементы приняты с ошибкой). Поэтому
а является
показателем группирования. Для реальных
каналов а=0,3... ... 0,7, а р=10-3...
10-5.
Распределение ошибок суммарной кратности
в
комбинациях разной длины
1
— появления групповых ошибок (при а= 1
вероятность искажений
комбинации не зависит от n,
так как в каждой ошибочной комбинации
все элементы приняты с ошибкой). Поэтому
а является
показателем группирования. Для реальных
каналов а=0,3... ... 0,7, а р=10-3...
10-5.
Распределение ошибок суммарной кратности
в
комбинациях разной длины
 .
.
Задача 1.24. При передаче дискретных сообщений по KB радиотелеграфному каналу блоками длиной 127 элементов определить вероятность появления в блоке четырех и более ошибок, если известны р=1,31•10-2 и а=0,448.
Решение. Вероятность .

Рассмотренные модели источников ошибок не учитывают нестационарность потока ошибок в каналах {часовые, дневные и недельные вариации). Поэтому с точки зрения адекватности модели реальным каналам наиболее перспективной следует считать модель дискретного канала с переменными параметрами [5.35]
Дополнительная литература 2[ 58-66], 6 [73-80].
Контрольные вопросы:
-
Модель канала с памятью
-
Модель канала без памятью
-
Симметричный канал.
-
Модель Маркова.
-
Модель Гильберта.
Лекция №7 (2 час.)
Узкополосная передача.
Важнейший параметр систем цифровой связи — отношение сигнал/шум
Любой,
кто изучал аналоговую связь, знаком с
критерием качества, именуемым отношением
средней мощности сигнала к средней
мощности шума (S/N
или SNR).
В цифровой связи в качестве
критерия качества чаще используется
нормированная версия SNR,
 .
. —
это энергия
бита, и ее можно описать как мощность
сигнала S,
умноженную
на время передачи
бита
—
это энергия
бита, и ее можно описать как мощность
сигнала S,
умноженную
на время передачи
бита
 .
.
 —
это
спектральная плотность мощности шума,
и ее можно выразить как мощность шума
N,
деленную
на ширину полосы W.
Поскольку
время передачи бита и скорость
передачи битов
—
это
спектральная плотность мощности шума,
и ее можно выразить как мощность шума
N,
деленную
на ширину полосы W.
Поскольку
время передачи бита и скорость
передачи битов
 взаимно
обратим,
взаимно
обратим,
 можно
заменить на
можно
заменить на

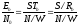 (7.1)
(7.1)
Еще
одним параметром, часто используемым
в цифровой связи, является скорость
передачи данных в битах в секунду. В
целях упрощения выражений, встречающихся
в книге, для представления скорости
передачи битов вместо записи
 будем
писать просто R.
С
учетом сказанного перепишем, выражение
(3.29) так, чтобы было явно видно, что
отношение
будем
писать просто R.
С
учетом сказанного перепишем, выражение
(3.29) так, чтобы было явно видно, что
отношение
 представляет
собой отношение S/N,
нормированное
на ширину полосы и скорость передачи
битов:
представляет
собой отношение S/N,
нормированное
на ширину полосы и скорость передачи
битов:
 (7.2)
(7.2)
Одной
из важнейших метрик качества в системах
цифровой связи является график
зависимости вероятности появления
ошибочного бита
 от
от
 .
На
рис. 7.6 показан "водопадоподобный"
вид большинства подобных кривых. При
.
На
рис. 7.6 показан "водопадоподобный"
вид большинства подобных кривых. При
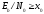 ,
,
 .
Безразмерное
отношение
.
Безразмерное
отношение
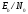 —
это
стандартная качественная мера
производительности систем цифровой
связи. Следовательно, необходимое
отношение
—
это
стандартная качественная мера
производительности систем цифровой
связи. Следовательно, необходимое
отношение
 можно рассматривать как метрику,
позволяющую сравнивать качество
различных систем; чем меньше требуемое
отношение
можно рассматривать как метрику,
позволяющую сравнивать качество
различных систем; чем меньше требуемое
отношение
 ,
тем
эффективнее процесс детектирования
при данной вероятности ошибки.
,
тем
эффективнее процесс детектирования
при данной вероятности ошибки.

для
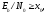


Рис.7.1.
Общий вид зависимости
 от
от

Низкочастотная демодуляция/детектирование
