3 Численные методы решения задач нелинейного программирования

3.1 Графический метод решения задач нелинейного программирования

Рассмотрим задачу нелинейного программирования, содержащую только две переменные, записанную в виде

,

…………….

(x)<,x= ().

Как уже отмечалось, функция f(x) называется целевой функцией, а неравенства,i= 1, ...,mназываются ограничениями задачи. Множество точек, удовлетворяющих ограничениям задачи, называется допустимым множеством задачи.

Решить задачу нелинейного программирования графически — значит найти такую точку из допустимого множества, через которую проходит

линия уровня f(,) = С, имеющая максимальное значение величины С из всех линий уровня, проходящих через допустимые точки задачи.

Как и в случае задач линейного программирования, для задач нелинейного программирования, содержащих только две переменные, возможна графическая интерпретация.

Наиболее существенное отличие задачи нелинейного программирования от линейных задач заключается в том, что оптимальное решение может находиться как на границе допустимого множества, так и являться его внутренней точкой.

Этапы графического решения задач нелинейного программирования

можно сформулировать следующим образом.

Этап 1. На плоскости наносятся геометрические места точек, соответствующих каждому уравнению из ограничений задачи (x) =,

i= 1, ...,m. Строится допустимое множество задачи. Если допустимое

множество задачи пусто, то задача не имеет решения.

Этап 2. Строятся линии уровня целевой функции f(,) = С при

различных значениях параметра С.

Этап 3. Определяется направление возрастания (для задачи максимизации) или убывания (для задачи минимизации) линий уровня целевой функции.

Этап 4. Определяется точка допустимого множества, через которую проходит линия уровня с максимальным (для задачи максимизации) или минимальным (для задачи минимизации) значением параметра С. Если целевая функция не ограничена сверху (для задачи максимизации) или не ограничена снизу (для задачи минимизации) на допустимом множестве, то задача не имеет решения.

Этап 5. Для найденной точки определяют ее координаты

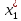=(,)и значение целевой функции в данной точкеf=(,)

Решим следующую задачу нелинейного программирования, используя геометрическую интерпретацию

,

.

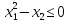Построим линии, соответствующие ограничениям задачи и вычислим область определения функции (рис. 3.1).

Рисунок 3.1 –Область определения функции

Рисунок 3.2 –Линия уровня функции

Линия уровня, соответствующая максимальному параметру С и проходящая через какую-либо точку допустимого множества, изображена на рисунке 3.2 АА’. Координаты оптимальной точки находятся из системы уравненийоткуда.

3.2 Метод множителей Лагранжа

Пусть требуется решить задачу нелинейного программирования следующего вида:

F(,

,

где функции fи,i=непрерывны, и непрерывны их частные производные по,l=.

Для решения поставленной задачи может быть применен метод множителей Лагранжа. Объясним идею метода на примере задачи нелинейного программирования, зависящей от двух переменных и имеющие только одно ограничение:

g=b.

Будем исходить из геометрической интерпретации задачи. А именно, заметим, что линия уровня с максимальным значением параметра С будет касаться линии границы в точке, являющейся оптимальным решением задачи (рис. 3.3).

Рисунок 3.3 –Геометрическая интерпретация задачи

Поскольку две гладкие линии (имеющие непрерывные частные производные) касаются друг друга в точке , то их векторы-нормали сонаправлены. Поскольку вектор-нормаль есть градиенты функций (вектор частных производных), то справедливо векторное соотношениеf’()=λg’(), гдеλесть некоторый коэффициент пропорциональности. Координаторами векторовf’() иg’(), являются значения частных производных функций f иgсоответственно в точке.

f’()=

g’()=

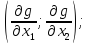
Из условия пропорциональности в точке имеем

;

.

Для определения значений ив которых функцияfдостигает максимума, к этим уравнениям надо добавить условие принадлежности точкиграфику функции g(,)=b.

Окончательно получаем систему уравнений, определяющую оптимальное решение поставленной задачи

Введем новую функцию

F

Тогда последняя система перепишется в виде

Функцию Fназьюают функцией Лагранжа.

Приведем ниже алгоритм метода множителей Лагранжа решения задач нелинейного программирования.

Этап 1. Составляют функцию Лагранжа

F()=f(.

Этап 2. Находят частные производные функции Лагранжа по и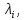

i=1,n;j=1,mи приравнивают их к нулю

.

Этап З. Решают систему и определяют точки, в которых функция может иметь экстремум.

Этап 4. Проверяют полученные на этапе 3 точки на экстремум и определяют экстремальное значение функции fнайденной точки.

Рассмотрим применение изученных методов на примере решения задачи оптимальной реализации продукции, в частности для расчета экономико-математической модели при нелинейных затратах на производство. Фирма реализует автомобили двумя способами: через магазин и через торговых агентов. При реализации автомобилей через магазин расходы на реализацию составляют 4усл. ед., а при продажеавтомобилей через торговых агентов расходы составляютусл. ед. Найти оптимальный способ реализации автомобилей, минимизирующий суммарные расходы, если общее число предназначенных для продажи автомобилей составляет 200 шт.

Составим математическую модель задачи. Целью является

минимизация суммарных расходов R=4.

Управляющие переменные- это число автомобилей, реализуемых первым и вторым способом: исоответственно (200 шт.).

Окончательно математическая модель имеет следующий вид:

R=4,

Для ее расчета применим метод множителей Лагранжа. Функция Лагранжа имеет вид

F(4+λ(200-.

Найдем частные производные функции Fпо,иλи приравняем их к нулю.

Получим следующую систему уравнений:

Решая систему, найдем 99,= 101,= 202,f() = 20 398.

Таким образом, для получения минимальных расходов, нужно реализовать 99 автомобилей через магазин и 101 автомобиль через торговых агентов. При этом расходы на реализацию составят 20 398 усл. ед.