
- •19 Экстремум функции. Необходимое усл.
- •20. Исследование функции.
- •21. Первообр. Функции и неопр. Интеграл. Св-ва неопр. Инт. Таблица неопр. Интегр.
- •31. Линии уровня. Градиент.
- •22. Интегрирование по частям и замена переменных в неопределённом интеграле.
- •23. Опред. Интеграл. Осн. Свойства опред. Интеграла.
- •24 Теорема Ньютона-Лейбница.
- •25.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной
- •26.Площадь плоской фигуры. Объем тела вращения.
- •27. Несобственныеинт. 1го и 2го порядка.
- •28. Среднее значение ф-и на отрезке. Теорема о среднем значении ф-и.
- •30. Экстремум ф-и нескольких переменных. Необходимое усл-е эктремума.
- •29. Ф-и нескольких переменных.
- •32. Частные производные ф-й 2-х переменных.
- •33. Полный дифференциал ф-й 2-х переменных.
- •34. Частные производные высших порядков.
- •35. Независимость частных производных от порядка дифференцирования.
- •36. Метод наименьших квадратов.
- •37. Числовые ряды, частные суммы числовых рядов.
- •38. Признаки сходимости ряда
- •39. Теоремы о сходимости числовых рядов.
- •40. Эталонные ряды для установления сходимости
- •41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена
- •42.Теорема Абеля о сходимости степенного ряда:
- •43.Разложение основных элементарных функций.
- •44. Показательная и тригонометрическая функция комплексной переменной, их связь
- •45. Ряд Фурье. Коэффициенты ряда Фурье. Сходимость рядов Фурье.
- •46. Дифференциальные уравнения (основные понятия)
- •47. Дифференциальныеур-я 1-го порядка с разделяющимися переменными:
- •48. Однородные дифференциальные уравнения
- •49. Линейные дифференциальные уравнения с постоянными коэффициентами
22. Интегрирование по частям и замена переменных в неопределённом интеграле.
Интег. по частям — один из способов
нахожд. интеграла. Суть метода: если
подынтегральная функция может быть
представлена в виде произвед. двух непр.
и гладких функций (каждая из которых
может быть как элементарной функцией,
так и композицией), то справедлива
следующая формула для неопределённого
интеграла:
![]()
Для упрощения вычисления интеграла
часто удобно выполнить замену переменной.
Переход от x к новой переменной u
описывается выражением
![]()
где x = g (u) - подстановка. Соответственно, обратная функция u = g −1(x) описывает зависимость новой переменной от старой.
дифф. dx должен быть заменен на дифф. новой переменной du. Для опред. инт., необход. также измен.пределы интегр-ния.
23. Опред. Интеграл. Осн. Свойства опред. Интеграла.
Определенный интеграл - это функция,
производная от которой дает подынтегральную
функцию. ОИ ф-цииy=f(x)
на отрезке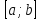 наз-ся предел инт-ых сумм.
наз-ся предел инт-ых сумм.
Свойства:
Свойства определённого интеграла:
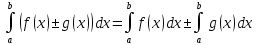
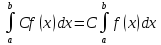

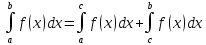
 ,
то
,
то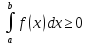
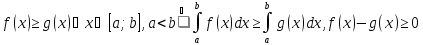
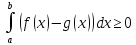
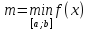 ,
,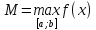 ,
то
,
то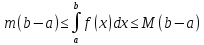
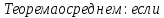 ф-я
ф-я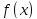 непрерывна на отрезке
непрерывна на отрезке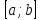 ,
,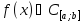 ,то
на этом отрезке сущ. хотя бы одна точка
,то
на этом отрезке сущ. хотя бы одна точка ,
,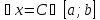 такая,
что
такая,
что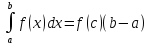
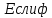 −я
−я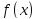 непрерывна
и
непрерывна
и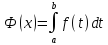 ,то
имеет место равенство
,то
имеет место равенство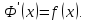 Ф-я
Ф-я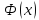 наз.
определённым интегралом с переменным
верхним пределом.
наз.
определённым интегралом с переменным
верхним пределом.
24 Теорема Ньютона-Лейбница.
Теорема: Опред. интеграл от непрерывной
ф-ции равен разности значений любой ее
первообразной для верхнего и нижнего
предела интегрирования. Формула
Ньютона-Лейбница связывает неопред и
опред интегралы. Если ф-цияy=f(x)
непрерывна на отрезке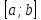 ,а
ф-цияF(x)-какая-либо
ее первообразная (т.е.F’(x)=f(x)),
то
,а
ф-цияF(x)-какая-либо
ее первообразная (т.е.F’(x)=f(x)),
то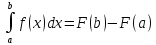 .
Эта формула сводит нахождение опрединтегр
к нахождению неопрединтегр. РазностьF(b)-F(a)
обозначаетсяF
.
Эта формула сводит нахождение опрединтегр
к нахождению неопрединтегр. РазностьF(b)-F(a)
обозначаетсяF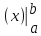 .
.
25.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной
Пусть функция у = f(х)
непрерывна на отрезке [a,b], а функцияx=φ(t),
определена на отрезке [α, β] и имеют на
нем непрерывную производную, причем φ
(α) = а, φ (β) =bи для всех .
Тогда
.
Тогда

Метод интегрирования по частям
Если функции u=u(x),v=v(x) имеют непрерывные производные на отрезке [a,b], то справедлива формула
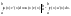 Доказательство.
Доказательство.
Поскольку функция u(x)v(x) – первообразная для функцииu’(x)v(x) +u(x)v’(x), то

откуда и следует формула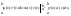 которую
можно записать в виде
которую
можно записать в виде
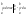
Формула интегрирования по частям для
определённого интеграла. Если u(x), v(x) -
непрерывно дифференцируемые функции,
то
![]() .
.
Необходимое условие интегрируемости.
Если функция интегрируема на отрезке, то она ограничена на нем.
Необходимое и дост. усл. интегрируемости.
Для того, чтобы ограниченная на некотором отрезке функция была интегрируема на нем необходимо и достаточно, чтобы lim∣τ∣→0(Sτ−sτ)=0
26.Площадь плоской фигуры. Объем тела вращения.
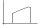
площадь Sкриволинейной
трапецииabAB, ограниченной
кривойy=f(x),f(x) 0
0
осью Oxи двумя прямымиx=ax=b,
вычисляется по формуле
y
y=f(x)
а
b
x
A
B
Если плоская фигура ABCDограничена прямымиx=a,x=b(a<b)
и кривымиy=f(x)y=φ(x), причем
φ(x)≤f(x),a≤x≤b,то
ее площадь вычисляется по формуле
y

x
A
B
C
D
y=φ(x)
y=f(x)
Объем тела, образованного вращением кривой y=f(x), ограниченной прямыми х = а,x=bприa<x<bвокруг оси Ох, вычисляется по формуле:
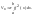
Объем тела, образованного вашей кривой у = φ(у), ограниченной прямымиy=c,y=dприc<y<dвокруг осиOy, вычисляется по формуле:
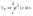
Центральный угол — это угол, образованный двумя радиусами. Длина дуги, описываемой концом радиуса, пропорциональна величине соответствующего центрального угла. Центральный угол дуги измеряется градусами. Для измерения градусами - целая окружность имеет 360°. Длина дуги
p=2π r n\360=π r n\180
