
- •19 Экстремум функции. Необходимое усл.
- •20. Исследование функции.
- •21. Первообр. Функции и неопр. Интеграл. Св-ва неопр. Инт. Таблица неопр. Интегр.
- •31. Линии уровня. Градиент.
- •22. Интегрирование по частям и замена переменных в неопределённом интеграле.
- •23. Опред. Интеграл. Осн. Свойства опред. Интеграла.
- •24 Теорема Ньютона-Лейбница.
- •25.Замена переменной и интегрирование по частям в определенном интеграле. Метод замены переменной
- •26.Площадь плоской фигуры. Объем тела вращения.
- •27. Несобственныеинт. 1го и 2го порядка.
- •28. Среднее значение ф-и на отрезке. Теорема о среднем значении ф-и.
- •30. Экстремум ф-и нескольких переменных. Необходимое усл-е эктремума.
- •29. Ф-и нескольких переменных.
- •32. Частные производные ф-й 2-х переменных.
- •33. Полный дифференциал ф-й 2-х переменных.
- •34. Частные производные высших порядков.
- •35. Независимость частных производных от порядка дифференцирования.
- •36. Метод наименьших квадратов.
- •37. Числовые ряды, частные суммы числовых рядов.
- •38. Признаки сходимости ряда
- •39. Теоремы о сходимости числовых рядов.
- •40. Эталонные ряды для установления сходимости
- •41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена
- •42.Теорема Абеля о сходимости степенного ряда:
- •43.Разложение основных элементарных функций.
- •44. Показательная и тригонометрическая функция комплексной переменной, их связь
- •45. Ряд Фурье. Коэффициенты ряда Фурье. Сходимость рядов Фурье.
- •46. Дифференциальные уравнения (основные понятия)
- •47. Дифференциальныеур-я 1-го порядка с разделяющимися переменными:
- •48. Однородные дифференциальные уравнения
- •49. Линейные дифференциальные уравнения с постоянными коэффициентами
27. Несобственныеинт. 1го и 2го порядка.
Инт-лы 1-го рода.
Предположим,
что функция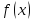 задана
на бесконечном промежутке вида
задана
на бесконечном промежутке вида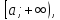 и интегрируема на любом конечном отрезке
и интегрируема на любом конечном отрезке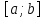 ,
где
,
где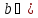 .
Таким образом, мы можем рассмотреть
функцию
.
Таким образом, мы можем рассмотреть
функцию ,
Если эта ф-ция имеетlim
,
Если эта ф-ция имеетlim![]() то числоIназ-ся значением
несобственного инт. 1го рода.
то числоIназ-ся значением
несобственного инт. 1го рода.![]() ,
а сам инт-л
,
а сам инт-л![]() называетсясходящимся.Если
же предела
называетсясходящимся.Если
же предела ![]() не
существует (например, если
не
существует (например, если ![]() при
при ![]() ),
то интеграл
),
то интеграл ![]() называется расходящимсяи
не имеет никакого числового значения.
называется расходящимсяи
не имеет никакого числового значения.
Несобств. инт-л 1-го рода – это инт-л, у кот.хотя бы 1 из пределов нтегрир-я = - или + ∞
Инт-лы 2го рода.
Пусть
функция f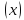 удовлетворяет указанным выше условиям
на [a;b).
Несобственным интегралом второго
рода назовём тогда интеграл
удовлетворяет указанным выше условиям
на [a;b).
Несобственным интегралом второго
рода назовём тогда интеграл![]() ,
значениеI которого
равняется левостороннему пределу
,
значениеI которого
равняется левостороннему пределу
![]() .Если этот предел
существует, то несобственный интеграл
называется сходящимся,
а если предела не существует,
то расходящимся.
Расходящемуся интегралу не приписывается
никакого числового значения; в этом
случае будем условно писать
.Если этот предел
существует, то несобственный интеграл
называется сходящимся,
а если предела не существует,
то расходящимся.
Расходящемуся интегралу не приписывается
никакого числового значения; в этом
случае будем условно писать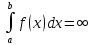 .
.
28. Среднее значение ф-и на отрезке. Теорема о среднем значении ф-и.
Средн. знач-е ф-и на отр-ке от а
до bназ. число:
С=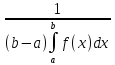 ;
;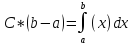
Теорема:Ср. знач-е ф-и на отрезке находится между миним. и макс-м значением ф-и. Т.е.m≤C≤M.
Док-во:когда ф-я положителна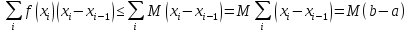

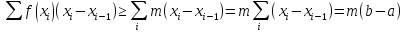

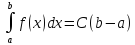
m≤C≤M
30. Экстремум ф-и нескольких переменных. Необходимое усл-е эктремума.
Глоб. максимум(наиб. значение ф-и в некот. обл-ти)-то ее знач-е, кот. больше любого др. знач-я в этой же обл-ти.
Глоб. минимум(наим. знач. ф-и в некот. обл-ти)-такое знач-е, кот-е меньше люб. др. знач-я в этой же обл-ти.
У глоб. макс. и мин-ов есть общ-е название-экстремумы ф-и.
Необх. усл-е:ф-я многих переменных может иметь экстремум только в точках, в кот.все её частные произв-ые=0. Такие точки назыв. критическими.
29. Ф-и нескольких переменных.
Ф-я 2х переменных– правило, кот.одному элементу из множестваxиyэлемент множестваz.
Для ф-и неск. переменных областью определениякаждого из аргументов наз. множество всех значений аргументов, для кот.имеет смысл заданная ф-я.
1)Определение. Если каждой паре (x,y) значений двух независимых переменных из области W ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y).
z=f(x,y)
2)Геометрическое изображение функции двух переменных - поверхность.
3)Частное и полное приращение функции.
Полное приращение функции
Dz=f(x+Dx, y+Dy)-f(x,y)
Частное приращение функции
Dx z=f(x+Dx)-f(x,y)
Dy z=f(x,y+Dy)-f(x,y)
Вообще, полное приращение функции не равно сумме частных приращений. Пример. z=xy.
Dx z=(x+Dx)y-xy=yDx
Dy z=x(y+Dy)-xy=xDy
Dz=(x+Dx)(y+Dy)-xy=yDx+xDy+DyDx № Dyz+Dx z.
4)Непрерывность функции нескольких переменных
Предел функции.
Пусть z=f(x,y) определена в некоторой окрестности A(x0,y0).
Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству |AP| < d, имеет место неравенство |f(x,y)-b| < e.
5)Непрерывная функция
6)Частные производные
32. Частные производные ф-й 2-х переменных.
Пусть задана функция f(x, y). Тогда
каждая из ее частных
производных![]() и
и![]() ,
которые называются также частными
производными первого порядка, снова
являются функцией независимых
переменных x, y и может, следовательно
также иметь частные производные. Частная
производная
,
которые называются также частными
производными первого порядка, снова
являются функцией независимых
переменных x, y и может, следовательно
также иметь частные производные. Частная
производная![]() обозначается
через
обозначается
через![]() или
или![]() ,
а
,
а![]() через
через![]() или
или![]() .
Таким образом,
.
Таким образом,
![]() ,
,![]()
и, аналогично,
![]() ,
,![]() .
.
Производные ![]() и
и![]() называются частными
производными второго порядка. Определение:Частной
производной второго порядкаот функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможныечастные
производные третьего порядка:
называются частными
производными второго порядка. Определение:Частной
производной второго порядкаот функции
z=f(x;y) дифференцируемой в области
D,называется первая производная от
соответствующей частной производной.
Рассматривая частные производные от
них, получим всевозможныечастные
производные третьего порядка:![]() ,
,![]() ,
,![]() и т. д.
и т. д.
Производные второго и более высокого порядков наз. произв-ми высших порядков.
