Студентам ИТ / 2 УПП_ИТ / Основн_литература / ИТ (Excel) / ИТ_автоматич_управл

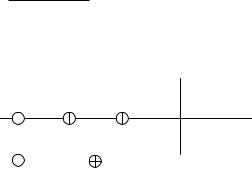
	(s 3) y0
Y(s) =	(s 1)(s 2) .	(1.3.10)

Положение полюсов и нуля этой функции на s-плоскости показано на рис. 1.3.1, где s = + j

				j
-3	-2	-1	0

- нуль, - полюс

Рис. 1.3.1

В общем случае, разложив (1.3.9) на элементарные дроби, получим

Y(s) =	k1		k2		,	(1.3.11)
	s s		s s
	1			2

где k1 и k2 – коэффициенты разложения, называемые вычетами. Теперь применим к (1.3.11) обратное преобразование

Лапласа

y(t) = L-1{

k1

k2

}= L-1{

k1

}+L-1{

k2

}.

s s

s

s

2

s s

s s

2

1

1

(1.3.12)

С помощью таблицы 1.3.1 находим решение

y(t) = k1exp(s1 t) + k2 k1exp(s2 t)

(1.3.13)

уравнения (2.1.3) в отсутствии входного воздействия, т.е., так называемое, свободное движение системы.

Часто бывает необходимо определить установившееся,

или конечное, значение y(t). Теорема о конечном значении

гласит, что:
lim y(t) limsY(s)		(1.3.14)
t	s 0

где допускается наличие простого полюса Y(s) в начале координат s-плоскости (см. рис. 1.3.1), но не допускается наличие полюсов на мнимой оси и в правой полуплоскости, а также – кратных полюсов в начале координат.

21

Для примера 1.3.1 lim y(t) limsY(s) =0. Тем самым, сво-

t

s 0

бодное движение стремится к конечному значению y(t) = 0. Передаточные функции линейных систем.

Передаточная функция линейной системы определяется как отношение преобразования Лапласа выходной переменной к преобразованию Лапласа входной переменной при условии, что все начальные значения равны нулю.

Передаточная функция существует только для линейных стационарных (с постоянными параметрами) систем и однозначно описывает динамическую связь между выходными и входными переменными.

Передаточная функция системы (2.1.3) получается, если в исходном уравнении (1.3.5) все начальные значения положить равными нулю

	Bs2Y(s) + CsY(s) + DY(s) = X(s).								(1.3.15)
	Отсюда находим передаточную функцию
	G(s)	Выход		Y (s)			1		(1.3.16)
		Вход		X (s)		Bs 2	Cs D

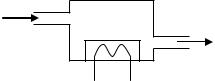
Пример 1.3.2. Передаточная функция RC цепи, изображенной на рис. 1.3.2, получается путем записи в операторной форме уравнений Кирхгофа для напряжений

U1(s) = [R +1/Cs] I(s),

(1.3.17)

U2(s) = I(s) / Cs.

u1(t)

u2(t)

i(t)

R

C

Рис. 1.3.2

Тогда из (1.3.17) следует, что

Выход U2

(s)

1

1

1/

,

(1.3.18)

Вход

U1

(s)

RCs 1

s 1

s 1/

где = RC есть постоянная времени цепи.

22

Пример 1.3.3. Пусть на вход цепи, изображенной на рис. 1.3.1, подано ступенчатое напряжение c амплитудой U0 (t), где(t) – функция Хевисайда. Как будет изменяться напряжение на выходе цепи?

Так как U1(s) = U0/s (см. таблицу 1.3.1), то согласно (1.3.18)

U2(s) = U1(s)	1/	= U0	1 1/			= U0[	1		1	].
	s 1/
			s s 1/				s s 1/

В результате обратного преобразования Лапласа получим

u2(t) = U0 [1– exp(– t/ )].

(1.3.19)

Рассмотрим теперь поведение системы высокого порядка и найдем ее реакцию на входной сигнал после затухания собственного (свободного) движения.

Пример 1.3.4. Пусть дифференциальное уравнение движения системы имеет вид

y(n) + qn-1 y(n-1) +…+q0 y = pn-1 x(n-1) + pn-2 x(n-2) +…+p0 x, (1.3.20)

где y(t) есть реакция системы, а x(t) – возмущающая функция. Если все начальные значения равны нулю, то вместо диф-

ференциального уравнения (1.3.20) системы запишем его образ

по Лапласу
snY(s) + qn-1 sn-1Y(s) +…+ q0 =	(1.3.21)
= pn-1 sn-1X(s) + pn-2 sn-2X(s) +…+ p0 X(s).

Тогда реакция системы состоит из свободного движения, определяемого начальными условиями, и вынужденного движения, обусловленного входным возмущением

	Y(s) =	o(s)		p(s)	X (s) ,	(1.3.22)
		q(s)		q(s)

где o(s) есть полином системы, учитывающий начальные условия, а

q(s) = sn + qn-1 sn-1 +…+ q0,	(1.3.23)
p(s) = pn-1 sn-1 + pn-2 sn-2 +…+ p0.

Если представить изображение по Лапласу входного возмущения дробно-рациональной функцией

X(s) = m(s) , d (s)

то вместо (1.3.22) можно записать

23

Y(s) =

o(s)

p(s) m(s)

o(s)

(s)

(s)

=

(1.3.24)

q(s)

q(s) d (s)

q(s)

q(s)

d (s)

= Y1(s) + Y2(s) + Y3(s).

Обратное преобразование Лапласа дает

y(t) = y1(t) + y2(t) + y3(t),

(1.3.25)

где составляющие y1(t) и y2(t) обуславливают переходной процесс в системе, а составляющая y3(t) – установившееся движение системы.

Пример 1.3.5. Пусть нагревательная система, изображенная на рис. 1.3.3, имеет следующие параметры:

T1 – температура входного потока жидкости;

T2 – температура выходного потока жидкости;

T(s) = T2 – T1 – разность температур; С0 – удельная теплоемкость воды;

С1 – теплоемкость жидкости; Q – расход жидкости;

P(s) – тепловая мощность нагревательного элемента; R – тепловое сопротивление изоляции;

G(s) – передаточная функция системы, задаваемая соотношением

G(s) = T (s)		1		.
P(s)		C s (QC 1/ R)
		1	0

Требуется найти время переходного процесса системы – время остывания, а также вид динамики процесса.

T1

T2

Нагревательный

элемент

Рис. 1.3.3

Решение. По аналогии с примером 1.3.2 преобразуем передаточную функцию системы к виду

24

G(s) = T (s)			1/ C1			1/ C1	,	(1.3.26)
P(s)		s QC / C 1/ RC				s 1/
	0		1	1

где = RC1/(1+RC0Q). Таким образом, динамика процесса остывания будет иметь вид T(t) exp(-t/ ).

Структурные схемы.

Для описания системы с несколькими управляемыми переменными используется структурная схема с перекрестными связями. Например, в системе на рис. 1.3.4 имеются две входных и две выходных переменных.

	X1(s)		Y1(s)
		Система
	X2(s)		Y2(s)
		Рис. 1.3.4

С помощью передаточных функций можно связать выходы и входы

Y1(s) = G11	X1(s) + G12	X2(s),	(1.3.27)
Y2(s) = G21 X1(s) + G22 X2(s),

где Gkm – передаточная функция от m-го входа к k-му выходу. Структурная схема, отражающая зависимости (1.3.27) приведена на рис. 1.3.5.

			+
	G11(s)			Y1(s)
X1(s)			+
	G12(s)
	G12(s)
X2(s)			+	Y2(s)
	G22(s)
			+
	Рис. 1.3.5
	25

Методы преобразования структурных схем основаны на рассмотрении алгебраических соотношений между отдельными переменными. Например, рассмотрим структурную схему отрицательной обратной связи, изображенную на рис. 1.3.6.

X(s) +		E(s)					Y(s)
					G(s)
-
					R(s)
		Z(s)
							Y(s)

Рис. 1.3.6.

Очевидно, что

E(s) = X(s) – Z(s) = X(s) – R(s) Y(s), Y(s) = G(s) E(s).

	Тогда		Y (s)		G(s)	.	(1.3.28)
		П(s) X (s)			1 G(s)R(s)

Выражение (1.3.28) представляет собой передаточную функцию замкнутой системы регулирования.

Структурные схемы дают гораздо лучшее представление о системах управления, чем описывающие их дифференциальные уравнения.

Пример 1.3.6. Пусть замкнутая система регулирования имеет большой коэффициент усиления G(s) R(s) > 1. Тогда передаточная функция системы полностью определяется передаточной функцией R(s) обратной связи и не зависит от передаточной функции G(s) объекта управления

	Y (s)		G(s)		G(s)		1	.	(1.3.29)
	X (s) 1 G(s)R(s)				G(s)R(s)		R(s)

С другой стороны, если необходимо синтезировать такую передаточную функцию R(s) отрицательной обратной связи, чтобы выход системы всегда воспроизводил ее вход, т.е. Y(s) = = X(s), необходимо, как следует из (1.3.28), чтобы

R(s) = 1–1/ G(s).

(1.3.29)

26

1.4. Модели линейных систем в виде сигнальных графов.

Для линейных систем достаточно сложной конфигурации Мейсоном предложен альтернативный метод взаимосвязи между переменными системы.

Сигнальный граф представляет собой диаграмму, состоящую из узлов, соединенных между собой отдельными направленными ветвями. Например, сигнальный граф, соответствующий уравнениям (1.3.27) и структурной схеме рис. 1.3.5 изображен на рис. 1.4.1.

G11(s)

X1(s) Y1(s)

	G21(s)
	G12(s)
X2(s)		Y2(s)
	G22(s)

Рис. 1.4.1.

Преобразование каждой переменной охарактеризовано надписью около направленной стрелки. Все ветви, выходящие из узла (кружок), передают сигнал другому (выходному) узлу каждой ветви. Сумма всех сигналов, входящих в узел, образует соответствующую этому узлу переменную. Путь – это ветвь или последовательность ветвей, которые могут быть проведены от одного узла к другому. Контур – это замкнутый путь, который начинается и заканчивается в одном и том же узле, причем, вдоль этого пути ни один другой узел не встречается дважды. Некасающимися называются такие контуры, которые не имеют общего узла. Два касающихся контура имеют один или более общих узлов.

Сигнальный граф – это просто наглядный метод записи системы алгебраических уравнений, показывающий взаимосвязь переменных. Например, рассмотрим следующую систему алгебраических уравнений

a11	x1	+ a12	x2	+ u1	= x1,	(1.4.1)
a21 x1 + a22 x2 + u2 = x2.

27

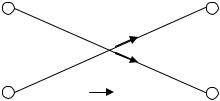
Здесь u1 и u2 – входные переменные, а x1 и x2 – выходные. Сигнальный граф, соответствующий уравнениям (1.4.1), изображен на рис. 1.4.2.

a11

1

u1 x1

a21 a12

1

u2 x2

a22

Рис. 1.4.2.

Записывая систему уравнений (1.4.1) в каноническом виде

(1- a11) x1 - a12 x2 = u1,

(1.4.2)

-a21 x1 + (1- a22) x2 = u2

ирешая ее по правилу Крамера, получим

x1 =	1 a22				u			a12		u			,	(1.4.3)
												2
				1
x2 =	a21		u			1 a11			u				,
											2
				1
где определитель системы уравнений
= 1 – a11 – a22 – a12 a21 + a11 a22.														(1.4.4)

Вданном случае определитель равен единице минус коэф-

фициенты передачи a11, a22 и a12 a21 отдельных контуров плюс произведение коэффициентов передачи двух некасающихся кон-

туров a11 и a22. Заметим, что контуры a11 и a21 a12 являются касающимися, также как, как и контуры a22 и a12 a21.

Врешении для x1 по отношению ко входу u1 числитель (1.4.3) равен значению определителя (1.4.4) не касающегося пу-

ти от u1 к x1. В решении для x1 по отношению ко входу u2 числитель (1.4.3) просто равен a12, т.к. этот путь касается всех контуров.

Вобщем случае передаточная функция П от входа X(s) к выходу Y(s) определяется формулой Мейсона

28

	Y (s)		K	Пk k
П(s)			k		,	(1.4.4)
	X (s)

где Пk – коэффициент передачи пути определяется как непрерывная последовательность ветвей, простирающихся в направлении, указанном стрелками, причем ни один узел не встречает-

ся в этой цепи более одного раза; – определитель графа; k – дополнительный множитель определителя для k-го пути. Причем,

= 1 – (сумма коэффициентов передачи всех отдельных контуров) + (сумма произведений всех возможных комбинаций из 2 некасающихся контуров) – (сумма произведений всех возможных комбинаций из 3 некасающихся контуров) + … .

Пример 1.4.1. На рис. 1.4.3 изображен сигнальный граф с двумя параллельными путями. Примером системы управления, граф которой имеет несколько путей, может служить распараллеленный конвейер. От входа X(s) к выходу Y(s) ведут следующие пути: путь 1 – П1 = G1G2G3G4 и путь 2 – П2 = G5G6G7G8.

	R2	R3
	L1	L2
G1	G2	G3	G4
X(s)			Y(s)
G5	G6	G7	G8
	L3	L4
	R6	R7

Рис. 1.4.3

Граф содержит четыре контура:

L1 = G2 R2, L2 = G3 R3, L3 = G6 R6, L4 = G7 R7.

Так как контуры L1 и L2 не касаются контуров L3 и L4, то

= 1 – (L1 + L2 + L3 + L4) + (L1L3 + L1L4 + L2L3 + L2L4).

Дополнительный множитель определителя для пути 1(2)

вычисляется в результате удаления из контуров, касающихся пути 1(2)

29

1 = 1 – (L3 + L4), 2 = 1 – (L1 + L2).

Таким образом

П(s) Y (s) П1 1 П2 2

X (s)

G1G2G3G4 (1 G6 R6 G7 R7 ) G5G6G7G8 (1 G2 R2 G3 R3 ) .

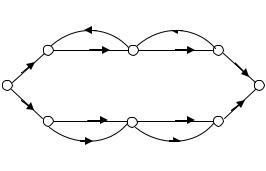
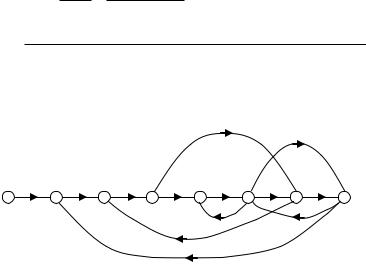
Пример 1.4.2. Сигнальный граф сложной системы с несколькими контурами и прямыми путями изображен на рис.

1.4.4.

				G7		G8
1	G1	G2	G3	G4	G5	G6
X(s)				-R4		Y(s)
						-R1
			-R2

-R3

Рис. 1.4.4

Прямые пути следующие:

П1 = G1G2G3G4 G5G6, П2 = G1G2G7G6, П3 = G1G2G3G4G8.

Кроме того имеются следующие контуры:

L1 = -G2G3G4G5G6R2, L2 = -G5G6R1, L3 = -G8R1, L4 = -G7R2G2, L5 = -G4R4, L6 = - G1G2G3G4G5G6R3, = -G1G2G7G6R3,

L8 = -G1G2G3G4G8R3.

Контур L5 не касается контура L4 или контура L7; контур L3 не касается контура L4; все остальные контуры являются касающимися. Поэтому определитель графа:

= 1 – (L1+L2+L3+L4+L5+L6+L7+L8) + (L5L7+L5L4+L3L4).

Дополнительные множители:

1 = 3 = 1 и 2= 1 – L5 = 1 + G4R4.

Следовательно,	Y (s)		П1 П2 2 П3
П(s) X (s)				.
	30