Студентам ИТ / 2 УПП_ИТ / Основн_литература / ИТ (Excel) / ИТ_автоматич_управл

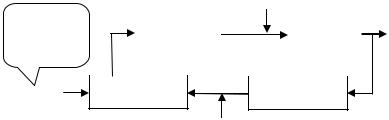
1.6.1 показана система регулирования, в которой присутствует как возмущение v(t), приложенное ко входу ТО, так и шум n(t)

измерительного устройства (датчика).
	e(t)			u(t)	v(t)
Желаемое
		Регулятор				ТО / ТП
значение
выхода
			y(t)
x(t)
	Сравнение				Измерение

Выход

n(t)

Рис. 1.6.1

Если передаточная функция ТО – GТО(s), передаточная функция датчика – GИ(s), передаточная функция регулятора – GР(s), а передаточная функция устройства сравнения – GУС(s), то к выходному сигналу y(t) системы добавляются сигналы, образы Лапласа которых имеют вид

Y		(s)			GУС (s)GР (s)GТО (s)					N (s) ,	(1.6.3)
	N				GУС
		[1				(s)GР (s)GТО	(s)GИ	(s)]
Y		(s)				GТО (s)				V (s) ,
	М
			[1 GУС			(s)GР (s)GТО	(s)GИ	(s)]

где N(s) и V(s) – образы Лапласа шума датчика и возмущения. Для достаточно большого коэффициента усиления регулятора будет выполняться условие GУС(s) GР(s) GТО(s) GИ(s) >> 1. Тогда,

Y		(s)	1				N (s) ,			(1.6.4)
	N
			GИ		(s)
Y		(s)				1		V (s)	1	V (s) , GУС 1.
	М
				GУС		(s)GР (s)GИ (s)			GР (s)GИ (s)

Для сигнала ошибки будем иметь в соответствии с (1.5.9)

		X (s)		V (s)		N (s)	.
	E(s)	GР (s)GТО (s)GИ (s) GР (s) GР (s)GТО (s)GИ (s)

(1.6.5)

41

Из (1.6.4) следует, что необходимо стремиться к увеличению передаточной функция датчика GИ(s), что эквивалентно максимизации отношения сигнал/шум на его выходе. Одновременно необходимо обеспечить большое значение коэффициента усиления обратной связи, т.е. GР(s) GИ(s) >> 1, чтобы снизить влияние возмущения на выходной сигнал.

Внимание! Следует помнить, что увеличение коэффициента усиления обратной связи может привести к нежелательному эффекту неустойчивости системы управления, или ухудшению ее качества.

Поэтому при синтезе систем управления необходимо обеспечить следующие цели:

1.Передаточную функцию П(s) с широкой полосой s пропускания и правильным воспроизведением входного эталонного сигнала x(t).

2.Контур обратной связи с большим усилением, чтобы минимизировать чувствительность Ч(s).

3.Большое усиление в контуре обратной связи за счет GР(s) GИ(s) т.е. регулятора и датчика.

Для этих целей синтезируют, так называемые, робастные системы управления. Робастная система управления должна обладать требуемым качеством несмотря на существенную неопределенность характеристик объекта управления.

Из рассмотренных в разделе 1.5 регуляторов лишь только ПИД-регулятор обладает свойствами, позволяющими настроить его на робастное управление.

В силу (1.5.5) ПИД-регулятор имеет передаточную функ-

цию

GР(s) = K1 + K2 / s + K3 s,

(1.6.6)

где K1 = k, K2 = k / TИ , K3 = k TД .

Для применения ПИД-регулятора к конкретному объекту управления надо настроить три коэффициента K1, K2 и K3.

ПИД-регуляторы особенно полезны для уменьшений установившейся ошибки и улучшения вида переходной характеристики, когда объект управления может быть аппроксимирован моделью второго порядка. Так, например, для ступенчатого входного воздействия X(s) = 1/s и N(s) = N0/s2 при s 0 (фликер-

шума) из (1.6.5) и (1.6.6) получим

e		N0	, т.е. e 0 для N0	0.	(1.6.7)
	K2GТО	(0)GИ (0)
			42

Переходные характеристики.

Типичная переходная функция системы второго порядка изображена на рис. 1.6.8.

y(t)
	M		1+d
1			C
0,9
			1+d
0,1
0	Tr	Tp	t
			Ts
			Рис. 1.6.8

Для описания данной функции используются следующие переходные характеристики:

-время нарастания Tr – время, необходимое для изменения переходной функции от 10% до 90% от ее установившегося значения, как показано на рис. 1.6.8;

-максимальное значение M переходной функции;

-время Tp достижения максимума;

-С – установившееся значение;

-максимальное относительное перерегулирование

(M–C)/C;

-время Ts установления – время, необходимое для того, чтобы выходной сигнал вошел в определенную зону, прилегающую к установившемуся значению, и далее оставался в пределах этой зоны. Ширину зоны 2d обычно принимают равной 10% или 4 % от установившегося значения C.

У системы второго порядка переходная функция обычно

входит в d = 2% зону за четыре постоянных времени , т.е. Ts = = 4 .

Пример 1.6.1. Стандартная форма передаточной функции системы второго порядка имеет вид

2
G(s) s2 2 s 2 ,	(1.6.8)

где – собственная частота колебаний при отсутствии затухания, – безразмерный коэффициент затухания.

43

Реакция системы (переходная функция) на единичное ступенчатое воздействие равна

	2		1	.	(1.6.9)
Y (s) s2 2 s 2 s

Обратное преобразование Лапласа дает (см. 1.3.13)

y(t) = 1 – (1/ ) exp(– t/ ) sin( t + ),

(1.6.10)

где = 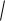1 2 , = arctg( / ), = 1/ – постоянная времени.

Используя результаты примера 1.6.1, можно показать, что для систем второго порядка важнейшие переходные характеристики определяются через физические параметры систем следующим образом

T					, M 1 exp(				) .	(1.6.11)
	p
				1 2		1 2

Частотные характеристики систем.

Предположим, что на вход системы с передаточной функцией G(s) подан синусоидальный сигнал

x(t) = A cos( t).	(1.6.12)
Тогда

X (s)	As	и
	s2 2

					As				As
	Y (s) G(s)						G(s)			.	(1.6.13)
			s2		2				(s j )(s j )
	Это выражение можно разложить на простые дроби
	Y (s)	k1				k2		G* (s) ,			(1.6.14)
		s j				s j

где G*(s) является функцией G(s) и обуславливает переходные процессы в системе в отсутствии внешнего воздействия. Поэтому установившееся движение определяется только двумя первыми членами выражения (1.6.14). Это означает, что в установившемся режиме реакция системы на синусоидальное воздействие также будет синусоидой той же частоты, т.е. при s = j

44

Y(j ) = k1 = G( j )	Aj		1		AG( j ) ,			(1.6.15)
	2 j
		2
Y(– j ) = k2 = G( j ) Aj						1	AG( j ) .
	2 j				2
Функция G(j ) является комплексной и называется ча-
стотной характеристикой системы
G(j ) = G(j ) exp(j ).								(1.6.16)

В соответствии с обратным преобразованием Лапласа выражения (1.6.14) реакция системы в установившемся режиме будет равна

Y(t) = k1 exp(j t) + k2 exp(–j t) =

=(A/2) G(j ) exp(j ) exp(j t) + + (A/2) G(–j ) exp(–j ) exp(–j t) =

=(A/2) G(j ) {exp[j( t+ )] + exp[–j( t+ )]} =

=A G(j ) cos( t + ),

поскольку G(–j ) = G(j ) .

Вопросы для самопроверки к главе 1.

1.В чем смысл отрицательной обратной связи? Что такое система регулирования?

2.Чем отличается автоматическая система управления от автоматизированной?

3.Перечислите и объясните основные этапы синтеза систем управления. Какой основной принцип управления заложен в процесс синтеза?

4.Изложите алгоритм исследования динамики физической системы.

5.В чем заключается принцип подобия при моделировании физических систем?

6.Динамика каких систем описывается дифференциальными, а каких разностными уравнениями? Приведите примеры.

7.Каким свойствам удовлетворяет линейная система? Объясните эти свойства.

8.В чем смысл преобразований Лапласа для линейных систем?

45

9.Как определяется установившееся значение выхода линейной системы?

10.Дайте определение передаточной функции линейной системы. Приведите пример.

11.Что такое структурная схема линейной системы?

12.Что такое сигнальный граф линейной системы? Приведите пример структуры и соответствующего сигнального графа. Зачем нужны сигнальные графы?

13.Объясните смысл формулы Мейсона для передаточной функции линейной системы.

14.Что такое регуляторы плавного действия? Приведите пример.

15.Что такое релейные регуляторы? Зачем они нужны?

16.Что такое закон регулирования? Перечислите известные Вам законы и объясните их.

17.В чем основные преимущества ПИД-регуляторов?

18.Изобразите графически отклик регуляторов на возмущение.

19.Какие критерии качества регулирования Вы знаете? Объясните их смысл.

20.Что такое робастное управление? Приведите пример робастной системы управления.

21.Какими переходными характеристиками описывается переходная функция систем второго порядка? Приведите примеры.

22.Как связаны переходные характеристики системы второго порядка с ее физическими параметрами.

23.Как определяется частотная характеристика

системы?

24. Kакова реакция линейной системы на синусоидальное воздействие? Чему равен коэффициент усиления гармонического сигнала?

25.Как связаны между собой аргумент s преобразования Лапласа и аргумент частотной характеристики линейной системы?

46

Глава 2. Цифровые системы управления

2.1. Дискретные сигналы и их z-преобразование.

Ниже на рис. 2.1.1 приведена функциональная схема одноконтурной цифровой системы управления. Компьютер в этой системе по определенной программе обрабатывает представленную в цифровой форме информацию и выдает на выходе сигнал также в цифровой форме. Программа может быть написана так, что качество системы в целом будет равно или очень близко к заданному. Многие компьютеры способны принимать и обрабатывать несколько входных сигналов, поэтому цифровые системы управления часто бывают многомерными.

ЦАП		Компьютер		АЦП
Датчик		ТП / ТО		ИУ

Рис. 2.1.1

Компьютер получает и обрабатывает сигнал в цифровом (численном) дискретном виде, а не в виде непрерывной переменной. В цифровой системе управления обязательно присутствует компьютер, входной и выходной сигнал которого представлены в виде числового кода. Преобразование непрерывного сигнала в цифровую форму осуществляет аналого-цифровой преобразователь (АЦП). Выходной сигнал компьютера (цифровой) преобразуется в непрерывную форму с помощью цифро-аналогового преобразователя (ЦАП). В результате любой непрерывный сигнал x(t) будет представляет собой

последовательность дискретных значений x(k t), где k = 0, 1, 2 целые числа.

Данные, получаемые о переменных системы только в дис-

кретные моменты времени и обозначаемые как x(k t), называются квантованными данными или дискретным сигналом.

Любое устройство, преобразующее непрерывный сигнал в дискретный, можно рассматривать как квантователь или ключ, ко-

торый замыкается каждые t секунд на бесконечно малый отрезок времени. Рассмотрим идеальный квантователь, изображенный на рис. 2.1.2. Его входной сигнал обозначен как x(t) а выходной – x*(t) =

= x(k t) (t – k t), где k t есть текущий момент замыкания, а (t) – единичная импульсная дельта-функция (Дирака).

47

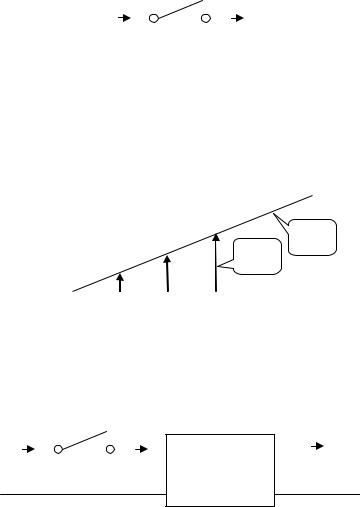
x(t)					x*(t)
Непрерывный			Дискретный
	сигнал			сигнал

Рис. 2.1.2

Предположим, что мы квантуем сигнал x(t), как показано на рис. 2.1.3, и получаем x*(t). Тогда дискретный сигнал x*(t) можно представить в виде последовательности импульсов (условно обозначенных вертикальными стрелками), начинающихся при t = 0, разделенных интервалами в t секунд и имеющих амплитуды x(k t).

x(t)		x*(t)
						x(3 t)				x(t)
		x( t)		x(2 t)				x*(t)
0		t		2 t		3 t		.		t

Рис. 2.1.3

Цифроаналоговый преобразователь – это устройство, которое преобразует дискретный сигнал x*(t) в непрерывный сигнал p(t). Обычно его можно представить в виде фиксатора (экстраполятора нулевого порядка, ЭПО), как показано на рис. 2.1.4.

			Экстраполятор
		x*(t)	нулевого
x(t)			порядка	p(t)

G0(s)

Рис. 2.1.4

Экстраполятор воспринимает значение x(k t) и сохраняет его постоянным на интервале k t < t < (k+1) t, как проиллюстрировано на рис. 2.1.5 для k = 0. Таким образом, значение x(k t) имеет место на выходе экстраполятора в течение всего периода квантования. Рис. 2.1.5 соответствует реакции экстраполяторнулевого порядка на единичный входной сигнал. При этом, передаточная функция экстраполя-

48

тора равна

G0 (s)	1 exp( s t)			.	(2.1.1)
		s
1

p(t)

0

t

2 t

3 t

.

t

Рис. 2.1.5

Квантователь и фиксатор могут достаточно точно воспроизводить входной сигнал, если только он незначительно изменяется за время, равное периоду квантования t. Реакция квантователя и фиксатора на линейный входной сигнал изображена ни рис. 2.1.6.

x(t) p(t)

x(t)

p(t)

0

t

2 t

3 t

.

t

Рис. 2.1.6

Z-преобразование дискретных сигналов.

Выходной сигнал x*(t) идеального квантователя представляет собой последовательность импульсов с амплитудами x(k t)

x* (t)	x(k t) (t k t) .		(2.1.2)
k 0
Преобразовав (2.6.2) по Лапласу (см.			1.3.1 стр. 19), полу-
чим
L{x* (t)}		x(k t)e ks t .	(2.1.3)
	k 0
		49

Это выражение представляет собой бесконечный ряд по

степеням члена es t. Введем переменную z = es t, возможно определить новое преобразование, называемое z-преобразованием

Z{x(t)} Z{x* (t)}			x(k t)z k .				(2.1.4)
		k 0
Пример 2.6.1. Найдем z-преобразование единичной сту-
пенчатой функции Xевисайда (t)
Z{x* (t)}	(k t)z	k		z k	z	.	(2.1.5)
k 0			k 0		z 1
В общем случае z-преобразование функции f(t) определя-
ется как
		f (k t)z k .					(2.1.6)
Z{ f (t)} F(z)
	k 0

Таблица 2.1.1 содержит z-преобразования часто встречающихся функций, а таблица 2.1.2 – его свойства. С более полной таблицей 2.1.1 можно познакомиться на сайте MCS.

				Таблица 2.1.1
x(t)		X(s)		X(z)
Ступенчатая функ-		1/s		z / (z–1)
ция Хевисайда,	(t)
Импульсная функция		1		1
Дирака
(t)
(t–k t)		exp(–k t)		z-k
t		1/s2		t z / (z–1)2
exp(– at)		1/(s + a)		z / [z–exp(–a t)]
1 – exp(– at)		1/s(s + a)		z [1– exp(–a t)] /
				(z-1)[z–exp(–a t)]
		2	2	z sin( t) /
sin( t)		/(s +	)	[z2–2zcos( t)+1]
cos( t)		s /(s2 + 2)		z [z – cos( t)] /
				[z2–2zcos( t)+1]
				z exp(–a t)sin( t) /
exp(-at) sin( t)		/[(s2 + a2) + 2]		[z2–2z exp(–a t)*
				*cos( t)+exp(–2a t)]
				z2 – z exp(–a t)*
exp(-at) cos( t)		(s + a)/[(s2 + a2) + 2]		*cos( t)/
				[z2–2z exp(–a t)*
				*cos( t)+exp(–2a t)]
		50