3. Методические указания к выполнению контрольной работы

Выполнение контрольных работ служит решению задачи получения студентами необходимых практических навыков по решению заданий из курса математики. Выполнение контрольных работ нацелено на получение студентами необходимых практических навыков решения задач из курса математического анализа. Прежде чем приступить к их выполнению, необходимо внимательно изучить соответствующие разделы Методических указаний, попробовав самостоятельно решить разобранные примеры.

В случае возникновения затруднений, а также при необходимости более глубокого изучения вопроса, следует обратиться к рекомендованной учебно-методической литературе.

Процесс работы над контрольной работой является важным этапом подготовки к зачету.

Номер выполняемой работы определяется путем деления шифра (номера зачетной книжки) на 20 и равен остатку, получающемуся при делении. Например, для зачетной книжки №1972 это вариант №12.

4. Контрольная работа №2Указания к заданию 1. Тема 1. Предел функции

Областью определения функции называют те значения, для которых данное выражение имеет смысл и значенияконечны.

Пусть функция определена в некоторой окрестности точки. Если для любого> 0 найдется такое число> 0, что при всех, удовлетворяющих неравенству, будет выполнено неравенство

, то число называютпределом функции в точке, то естьA=.

Число называетсялевосторонним пределом функции в точке, если для любого> 0 найдется такое число> 0, что при всех, удовлетворяющих неравенству, будет выполнено неравенство

. Левосторонний предел обозначают следующим образом: =.

Аналогично, число называетсяправосторонним пределом функции в точке, если для любого> 0 существует> 0, такое, что из неравенстваследуети =.

Например, для функции в точкеимеет смысл говорить только о левостороннем пределе, а для функциив точке─ только о правостороннем.

Можно доказать, что для существования предела функции в точкенеобходимо и достаточно, чтобы существовали и были равны левосторонний и правосторонний пределы в этой точке.

Если для любого существует> 0, такое, что при всехиз─ окрестностибудет выполнено условие, то предел функциив точкеравен бесконечности:.

Если же для любого существует, такое, что при всех, тоявляется пределом функциипри, стремящемся к бесконечности:.

Важным частным случаем последнего определения является предел числовой последовательности. Если функция задана на множестве натуральных чисел, то такую функцию называют числовой последовательностью(=), а ее предел ─ пределом последовательности Таким образом, число являетсяпределом последовательности, если для любогосуществует, такое, что привыполняется неравенство.

Отметим следующие свойства пределов:

1. Если существует, то он единственный.

2. (постоянное число);

3.

4.

5. ().

Дадим несколько определений, важных для дальнейшего.

Функция называетсябесконечно малой в окрестности точки , если. Функция называетсябесконечно большой в окрестности точки , если. Функция называетсяограниченной в окрестности точки , еслисуществует число , такое, чтопри всехиз этой окрестности.

Для вычисления пределов важны следующие свойства бесконечно малых величин. Пусть и─ бесконечно малые, а─ ограниченная функция в окрестности точки. Тогда верны утверждения:

1.─ бесконечно малая величина в окрестности точки;

2.─ бесконечно малая величина в окрестности точки;

3. ─ бесконечно малая величина в окрестности точки;

4. Если существует, то это равносильно тому, что в окрестности точки , где─ бесконечно малая величина в окрестности этой точки;

5. Для монотонно возрастающей функции (при) или монотонно убывающей (при) в окрестности точкивсегда существует, который конечен, если ограничена в окрестности точки.

Рассмотрим две бесконечно малые величины ив окрестности точки. Если, то говорят, что ─ величина более высокого порядка малости, чем. Записывают это следующим образом:. Если, то иназываютэквивалентными бесконечно малыми величинами в окрестности точки , то есть~.

Рассмотрим несколько примеров.

Пример1. Вычислить предел.

Решение. Очевидно, что числитель дроби при стремится к.Аналогично знаменатель стремится к .Тогда вся дробь будет стремиться к .Таким образом, .

Здесь мы использовали свойства пределов, о которых говорилось выше.

Пример2. Вычислить предел.

Решение. Очевидно, , апри. Таким образом, дробь будет стремиться к бесконечности, так как знаменатель ─ бесконечно малая величина, а обратная ей величина ─ бесконечно большая.

Поскольку числитель в окрестности точки ограничен, получаем:.

Пример3. Вычислить предел.

Решение. Если подставить в рассматриваемую функцию, получим ноль в числителе и знаменателе. Без дополнительных преобразований трудно сказать, к чему будет стремиться подобное выражение. Поэтому такие выражения называют неопределенностью вида. Встречаются также неопределенности вида,,,, для каждой из которых существуют свои способы вычисления пределов, то есть раскрытия неопределенности.

Вернемся к примеру. Разложим числитель на множители:

.

Рассмотрим , где и─ многочлены степении:

Пусть Разделим числитель и знаменатель почленно на

Нетрудно видеть, что при все слагаемые числителя, кроме последнего, стремятся к нулю, а в знаменателе все слагаемые стремятся к нулю. Таким образом, по аналогии с примером 2.

Если , то, а дробь в знаменателе имеет уже степень числителя большую, чем степень знаменателя и, согласно только что рассмотренному случаю, стремится к бесконечности. Тогда имеем:

так как величина, обратная бесконечно большой, есть бесконечно малая величина.

Рассмотрим теперь случай Поделив числитель и знаменатель почленно на, получим:

Таким образом,

Рассмотрим два предела: и .

С помощью несложных оценок можно показать, что Вычисление второго предела требует бóльших усилий, но можно доказать, что он равен числу (основанию натурального логарифма):. Доказательства можно найти в учебниках по математическому анализу.

В силу важности этих пределов их называют замечательными пределами. Используя замечательные пределы, можно получить следующие результаты:

;; ;

; .

Поэтому можно утверждать, что при ~, ~, ~, ~, ~, где знак ~ означает эквивалентность соответствующих бесконечно малых величин. При вычислении пределов можно использовать эти соотношения эквивалентности, заменяя, например, отношения бесконечно малых на отношения эквивалентных им бесконечно малых величин.

Пример 4. Вычислить предел:

.

Решение.

Очевидно, что все подкоренные выражения при стремятся к единице, а вторые слагаемые в скобках ─ к нулю. Поэтому последний предел равен следующему:

Пример 5. Вычислить предел .

Решение. Подставив в заданную функцию , убеждаемся, что имеем дело с неопределенностью вида. Известно, что если─ корень многочлена, то, где─ многочлен степени .

Следовательно, . Проще всего узнать вид многочлена, разделивна. Это можно сделать, выполнив деление «столбиком», как делят числа:

0

Следовательно, . Тогда, разлагая на множители разность кубов в знаменателе, получим:

Пример 6. Вычислить предел .

Решение. Это неопределенность вида . Домножим функцию, стоящую под знаком предела, на сопряженную сумму:

Пример7. Вычислить предел .

Решение.В данном случае имеем дело с неопределенностью вида. Преобразуем выражение в скобках, выделив единицу и бесконечно малую функцию:

Тогда

Так как при ─ бесконечно малая величина,

то

Поскольку , получаем:

Пример 8. Найти предел

Решение.Прирассматриваемая функция имеет неопределенность вида. Введем новую переменную. Когда переменная, переменная. Тогда рассматриваемый предел принимает вид:

так как ~, а.

Пример 9. Найти предел

Решение.Неопределенность вида. При~. Поэтому~.

Далее, ~ .

Поэтому

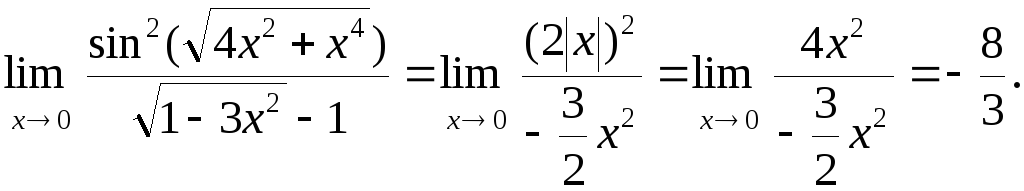
Пример10. Найти предел .

Решение.Неопределенность вида. Введем новую переменнуюТогда получим:

Здесь учтено, что ~при.

Контрольные задания

Найти следующие пределы.

1.1 а) б)

1.2. а) б)

1.3. а)б)

1.4. а) б)

1.5. а)б)

1.6. а) б)

1.7. а)б)

1.8. а) б)

1.9. а)б)

1.10. а) б)

1.11. а)б)

1.12. а) б)

1.13. а)б)

1.14. а) б)

1.15. а)б)

1.16. а) б)

1.17. а)б)

1.18. а) б)

1.19. а)б)

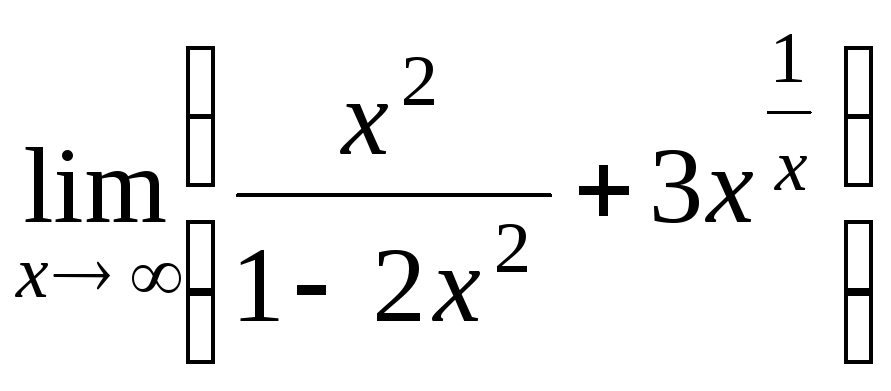1.20. а) б)

Указания к заданию 2. ТЕМА 2. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ

Пусть на интервале задана функция. Возьмем некоторое числои придадим аргументуприращение. Тогда значение функции получит приращение. Рассмотрим отношение. Если присуществует конечный предел дроби, то этот предел называютпроизводной функции в точкеи обозначают символом(или):

.

Нахождение производной называют дифференцированием функции.

Функцию называютдифференцируемой в точке , если в окрестности этой точки ее приращение может быть представлено в виде:

.

Можно доказать, что для дифференцируемости функции необходимо и достаточно, чтобы существовала и была конечной ее производная, при этом .

Выражение называютдифференциалом функции и обозначают . Приращение аргументаназывают дифференциалом независимой переменной и обозначают. Таким образом,.

Геометрически дифференциал есть приращение касательной, проведенной к графику функции в точке, и может быть как меньше, так и больше приращения функции. Для линейной функции

Если производная существует для всех из интервала, то тем самым производная определена как функцияв этом интервале, и можно говорить о производной от этой функции, называемой второй производной функции:Аналогично вводится понятие высших производных (производные, начиная со второй, называются производными высшего порядка).

Для освоения техники дифференцирования, то есть нахождения производных, необходимо использовать правила дифференцирования и таблицу производных наиболее часто встречающихся функций.

Основные правила дифференцирования

1. .

2. (– постоянная).

3.

4. .

5. Производная сложной функции: если , то, где производные функций в правой части равенства берутся по аргументамисоответственно.

Приведем таблицу производных наиболее часто используемых функций:

1. (– постоянная)

2.

3.

4. (– постоянная)

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

Логарифмической производной функции называется производная от логарифма этой функции: , при y > 0. Нахождение производных от многих функций значительно упрощается, если эти функции предварительно прологарифмировать, а затем воспользоваться логарифмической производной. При этом логарифмическую производную применяют формально, не учитывая, что формула имеет смысл лишь при y > 0.

Функция y(x) называется неявной, если зависимость между х и у выражена уравнением F(x,y)=0, неразрешенным относительно у.

Чтобы найти производную от неявной функции, надо данное уравнение продифференцировать, считая у функцией от х, а затем полученное уравнение решить относительно производной .

Рассмотрим примеры вычисления производных.

Пример 1. Найти производную функции .

Решение. Применяя правила 4,1 и таблицу производных, получим:

.

Пример 2. Найти , если.

Решение. Последовательно применяя правило дифференцирования сложной функции, получим:

Пример 3. Найти производную функции .

Решение. Применим логарифмическую производную:

Пример4. Найти производную функции .

Решение. В случае произведения нескольких сомножителей применение логарифмической производной также эффективно:

EMBED Equation.3 _.

Пример 5. Найти производную функции , если.

Решение. Применим правило дифференцирования неявной функции:

Контрольные задания

Найти производные функций, заданных в явном и неявном виде.

2.1.

2.2.

2.3.

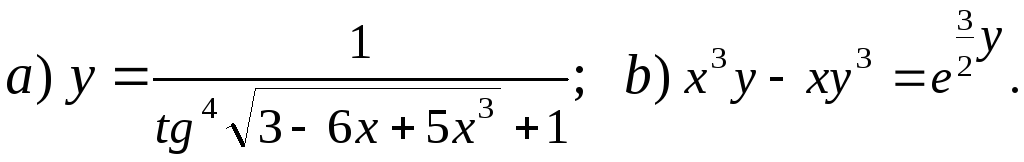
2.4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

2.11.

2.12.

2.13.

2.14.

2.15.

2.16.

2.17.

2.18.

2.19.

2.20.

Указания к заданию 3. ТЕМА 3. ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ГРАФИКА

Внутренняя точка интерваланазывается точкоймаксимума (минимума) функции , если существует такое, что для всехиз интервала, содержащегося внутри интервала, выполняется неравенство(). Точки максимума и минимума называютточками экстремума (локального экстремума) функции. Точки, в которых производная обращается в ноль, называют стационарными точками.

Приведем формулировки теорем, используемых при исследовании функций.

Достаточное условие строгого возрастания (убывания) функции.

Если () в интервале, тострого возрастает (убывает) в этом интервале.

Промежутки, в которых функция возрастает (убывает), называются промежутками монотонности функции. Чтобы найти промежутки монотонности функции необходимо:

1. найти область определения функции;

2. найти производную функции;

3. приравнять производную к нулю и определить ее корни (стационарные точки), а также найти точки, в которых производная не существует, а функция определена;

4. определить знак производной в каждом из промежутков, на которые разбивается полученными точками область определения функции.

Необходимое условие экстремума функции

Если функция дифференцируема в точкеи достигает в этой точке максимума (минимума), то.

Точками экстремума могут быть только те точки, в которых производная равна нулю, либо не существует. Точки, в которых производная равна нулю или не существует, на­зывают точками, подозрительными на экстремум, или критическими точками.

Достаточные условия экстремума функции

Если при переходе через точку , подозрительную на экстремум, производная меняет знак, то точкаявляется точкой экстремума. При этом если в некоторой окрестности точкидляидля, тоявляется точкой максимума. Если же в этой окрестностидляидля, то– точка минимума.

Другим достаточным признаком существования экстремума в стационарной точке является условие(тогда это точка максимума) и(тогда это точка минимума). При этом считается, чтоимеет непрерывную вторую производную в некоторой окрестности точки.

График функции называется выпуклым (или выпуклым вверх) в интервале , если он расположен не выше касательной проведенной в любой точке этого интервала (рис.1).

График функции называетсявогнутым (или выпуклым вниз) в интервале , если он расположен не ниже касательной, проведенной в любой точке этого интервала (рис. 1).

Рис. 1

Достаточные условия выпуклости (вогнутости) графика функции

Если в интервале, то график функции является выпуклым в этом интервале; если же , то в интервале график функции вогнутый.

Точка графика функции, отделяющая его выпуклую часть от вогнутой, называетсяточкой перегиба. Если ─ абсцисса точки перегиба графика функции , то вторая производная равна нулю или не существует в этой точке. Точки, в которых илине существует, называютсякритическими точками второго рода.

Если при переходе через критическую точку второго рода вторая производная меняет знак, то точкаесть точка перегиба.

Прямая l называется асимптотой кривой y = f(x), если расстояние точки М(х,у) на кривой от прямой l стремится к нулю при неограниченном удалении этой точки по кривой от начала координат, (т.е. при стремлении хотя бы одной из координат точки к бесконечности).

Прямая является вертикальной асимптотой кривой y = f(x), если:

или .

Прямая является горизонтальной асимптотой кривой y = f (x), если существует или .

Прямая является наклонной асимптотой кривой y = f(x), если существуют пределы:

или .

При исследовании функции и построении ее графика удобно придерживаться следующего плана.

1. Найти область определения функции.

2. Определить четность (нечетность), периодичность функции.

3. Найти точки разрыва.

4. Определить точки пересечения графика с осями координат.

5. Найти точки экстремума и вычислить значения функции в этих точках.

6. Определить интервалы возрастания и убывания функции.

7. Найти точки перегиба, интервалы выпуклости и вогнутости.

8. Определить асимптоты.

9. Найти предельные значения функции при аргументе, стремящемся к границам области определения.

В процессе исследования функции не обязательно строго придерживаться приведенной схемы.

Пример. Исследовать функцию и построить ее график.

Решение.

1. Данная функция определена и непрерывна на всей оси ОХ, за исключением точки , где она терпит бесконечный разрыв. Область определения функции

2. Поскольку и, то рассматриваемая функция не является ни четной, ни нечетной, то есть это функция общего вида. Функция непериодична.

3. Точка х=-1 является точкой разрыва.

4. Точка (0;0) является точкой пересечения функции с осями координат.

5. Точки экстремума.

Вычислим производную: .

Производная обращается в нуль при и.

Производная не существует при х=-1.

Точка ─максимум, а точка─минимум функции.

Построим интервалы монотонности (рис. 2):

Рис. 2

6. Функция возрастает при и убывает при.

7. Найдем вторую производную:

.

Вторая производная в нуль нигде не обращается, но при переходе через точку меняет свой знак с минуса на плюс. Следовательно, в интервалеграфик функции выпуклый, а в интервале ─ вогнутый. Точек перегиба функция не имеет.

8. Асимптоты функции.

Выясним, имеет ли функция наклонные асимптоты. ,

.

Следовательно, прямая является наклонной асимптотой при . Легко проверить, что эта же прямая является наклонной асимптотой при .

Построим график исследуемой функции (рис. 3):

Рис. 3

Контрольные задания

Исследовать функцию методами дифференциального исчисления и построить ее график.

3.1.. 3.2.

3.3. 3.4.

3.5. 3.6.

3.7. 3.8.

3.9. 3.10.

3.11. 3.12.

3.13. 3.14.

3.15. 3.16. .

3.17.. 3.18.

3.19. 3.20.

Указания к заданию 4. ТЕМА 4. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Рассмотрим функцию двух переменных , определенную в некоторой области, являющейся частью плоскостиЧастной производной от функции по независимой переменной х называется производная

вычисленная при постоянном у.

Частной производной по у называется производная

вычисленная при постоянном х.

Для частных производных справедливы обычные правила и формулы дифференцирования.

При изменении ичастные производные сами являются функциями, и можно вычислять частные производные от этих функций. Частные производные второго порядка обозначают следующим образом:

Последнюю из трех частных производных второго порядка называют смешанной производной. Если частные производные второго порядка непрерывны в точке , тогда, то есть не важно, в какой последовательности вычисляется смешанная производная.

Градиентом функции в точкеназывается вектор, составленный из частных производных:

Этот вектор указывает в точке М₀ направление наискорейшего роста функции .

Для функции двух переменных вводится понятие производной по направлению, аналогичное понятию частной производной, когда приращение аргумента задается вдоль данного направления. Для любого направления, задаваемого вектором , производная функциив точке по направлению этого вектора может быть выражена следующим образом:

где знак модуля означает длину вектора градиента в точке , а ─ угол между градиентом и направлением .

Пример. Найти градиент функции в точке.

Решение. Рассматривая у как постоянную величину, дифференцируем функцию по переменной х.

.

Аналогично, рассматривая х как постоянную величину, получаем:

.

Находим значения частных производных в точке :

,

Таким образом,

Контрольные задания

Найти градиент функции Z в точке М.

4.1 .

4.2

4.3

4.4

4.5

4.6

4.7

4.8

4.9

4.10

4.11

4.12

4.13

4.14

4.15

4.16

4.17

4.18

4.19

4.20

Указания к заданию 5. ТЕМА 5. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Функция называетсяпервообразной для функциина некотором промежутке, если для всех значенийиз этого промежутка выполняется равенство.

Например, функция является первообразной для функции, так как при любом.

Можно заметить, что первообразной дляявляется не только,но и функция+ С, где С ─ любая постоянная. Это справедливо для любой функции, имеющей первообразную.

Теорема.Пустьявляется первообразной для функциив некотором интервале; тогда функция, где С ─ любая постоянная, также будет первообразной для.

Из теоремы следует, что любые две первообразные для одной и той же функции могут отличаться друг от друга только на постоянное слагаемое.

Если ─ первообразная для функции, то совокупность всех первообразных, где С ─ произвольная постоянная, называетсянеопределенным интеграломот функциии обозначается символом. Таким образом,=.

Функция называется подынтегральной функцией, произведение─ подынтегральным выражением, переменная- переменной интегрирования, а символ- знаком интеграла.

Операция нахождения неопределенного интеграла от данной функции называется интегрированиемфункции_.Операция интегрирования является обратной к операции дифференцирования.