
- •«Рівняння з частинними похідними»
- •Перелік практичних занять
- •Завдання до теми
- •Завдання до теми
- •Завдання до теми
- •Завдання для перевірки знань:
- •Завдання до теми
- •Завдання до теми
- •Завдання до теми
- •Завдання для перевірки знань
- •Контрольні питання
- •Практичне заняття № 11
- •Короткі теоретичні відомості
- •Завдання до теми
- •Завдання до теми
- •Завдання для перевірки знань
- •Контрольні питання
- •Список літератури
- •39600, М. Кременчук, вул. Першотравнева, 20
Перелік практичних занять
Практичне заняття № 1
Тема Диференціальні рівняння в частинних похідних (ДРЧП) 1-го порядку. Загальний розв’язок
Мета: сформулювати уявлення про ДРЧП 1-го поряду, про лінійне і квазілінійне ДРЧП 1-го поряду, загальний розв’язок ДРЧП 1-го порядку. Навчитися знаходити загальний розв’язок ДРЧП 1-го порядку.
Короткі теоретичні відомості
Рівняння вигляду
![]() , (1)
, (1)
де
![]() – невідома функція, називається ДРЧП
1-го поряду.
– невідома функція, називається ДРЧП
1-го поряду.
Рівняння
![]() ,
(2)
,
(2)
де
a, b, c – неперервні функції в деякій
області G і задовольняють у ній умову
![]() ,
називається напівлінійним.
,
називається напівлінійним.
Щоб розв’язати рівняння (2) необхідно скласти та розв’язати систему звичайних диференціальних рівнянь (ЗДР)
![]() .
(3)
.
(3)
Загальним розв’язком рівняння (2) є функція
 ,
де
,
де ,
, – два лінійно незалежних інтеґрала
системи (3).
– два лінійно незалежних інтеґрала
системи (3).Завдання до теми
Знайти загальний розв’язок рівняння
![]() .
.
Розв’язування.
Запишемо систему рівнянь
![]() .
Скориставшись властивістю пропорції,
представимо рівняння
.
Скориставшись властивістю пропорції,
представимо рівняння![]() у вигляді
у вигляді
![]()
![]()
![]() .
.
Інтеґруючи, отримуємо
![]()
![]()
![]() .
.
Друге
рівняння системи
![]()
![]()
![]() .
.
Загальний розв’язок даного рівняння має вигляд:
![]() .
.
Завдання для перевірки знань
Знайти загальний розв’язок рівняння:
 .
Відповідь:
.
Відповідь:
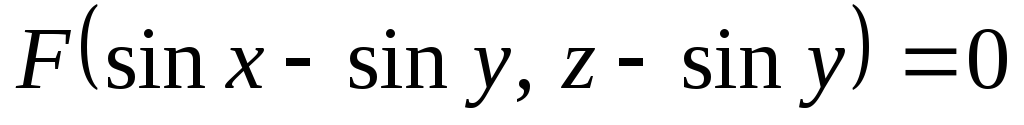 .
. .
Відповідь:
.
Відповідь:
 .
. .
Відповідь:
.
Відповідь:
 .
. .
Відповідь:
.
Відповідь:
 .
. .
Відповідь:
.
Відповідь:
 .
.
Контрольні питання
З якому випадку рівняння (1) називається квазілінійним?
Що таке пучки та вісі Монжа?
Які криві називають характеристичними?
Чи відрізняється загальний розв’язок ДРЧП 1-го порядку від загального розв’язку ЗДР?
Література: [1-5].
Практичне заняття № 2
Тема ДРЧП 1-го порядку. Задача Коші.
Мета: дати уявлення про задачу Коші для ДРЧП 1-го порядку, навчитися знаходити поверхню, яка задовольняє рівняння та проходить через лінію.
Короткі теоретичні відомості
Щоб
знайти поверхню
![]() ,
яка задовольняє рівнянню
,
яка задовольняє рівнянню
![]() (1)
(1)
та проходить через лінію
![]() (2)
(2)
спочатку необхідно знайти загальний розв’язок рівняння (1), тобто два лінійно незалежних інтеґрала
![]() і
і
![]() .
(3)
.
(3)
Потім у (3) необхідно підставити (2) та отримати систему рівнянь у вигляді
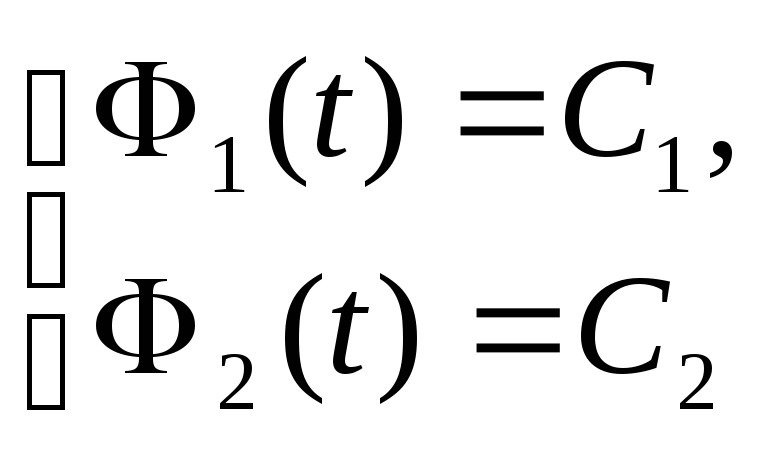 (4)
(4)
Систему
(4) можна переписати так:
![]() =0.
Підставивши в останнє рівняння замість
=0.
Підставивши в останнє рівняння замість![]() і
і![]() ліві частини виразів (3), ми отримуємо
розв’язок задачі Коші.
ліві частини виразів (3), ми отримуємо
розв’язок задачі Коші.
Завдання до теми
Знайти інтеґральну поверхню, яка задовольняє рівняння
![]()
та
проходить через криву
![]() .
.
Розв’язування.
Запишемо систему рівнянь
![]() та знайдемо
її перші інтеґрали:
та знайдемо
її перші інтеґрали:
![]() ,
,![]() .
.
Щоб
знайти інтеґральну поверхню, яка
проходить через криву
![]() ,
запишемо цю криву у параметричному
вигляді. Наприклад, візьмемо
,
запишемо цю криву у параметричному
вигляді. Наприклад, візьмемо![]() як параметр:
як параметр:![]() .
Підставляючи ці вирази у перші інтеґрали,
отримуємо
.
Підставляючи ці вирази у перші інтеґрали,
отримуємо![]() ,
,![]() .
Виключаючи
.
Виключаючи![]() ,
отримуємо
,
отримуємо![]() .
Підставляючи замість
.
Підставляючи замість![]() і
і![]() ліві частини перших інтеґралів, знайдемо
розв'язок даної задачі:
ліві частини перших інтеґралів, знайдемо
розв'язок даної задачі:
![]() .
.
Завдання для перевірки знань
Знайти розв’язок задачі Коші для ДРЧП 1-го порядку та зробити його перевірку.
 ,
,  ,
, .
.
Відповідь:
![]() .
.
 ,
,  ,
, .
.
Відповідь:
![]() .
.
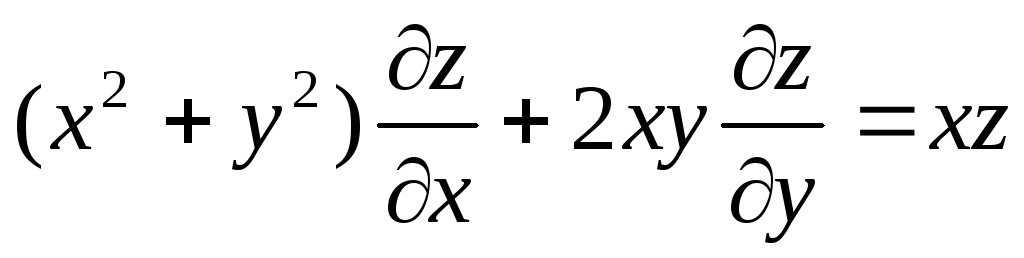 ,
,  ,
, .
.
Відповідь:
![]() .
.
 ,
,  ,
, .
.
Відповідь:
![]() .
.
Контрольні питання
Сформулюйте задачу Коші для ДРЧП 1-го порядку.
У якому випадку задача Коші має один і тільки один розв'язок?
У якому випадку задача Коші має нескінченну множину розв'язків?
Література: [1, 6].
Практичне заняття № 3
Тема Класифікація ДРЧП 2-го порядку та зведення до канонічного вигляду
Мета: засвоїти поняття про ДРЧП 2-го порядку, умови приналежності ДРЧП 2-го порядку до еліптичного, параболічного або гіперболічного типу. Виробити навички зведення ДРЧП 2-го порядку до канонічного вигляду.
Короткі теоретичні відомості
Диференціальним рівнянням у частинних похідних другого порядку з двома невідомими змінними називаються співвідношення між невідомою функцією u(x,y) та її частинними похідними до другого порядку включно, тобто
![]() .
.
ДРЧП 2-го порядку називається лінійним, якщо воно має вигляд:
![]() (1)
(1)
Уведемо нові змінні
 ,
, .
Перетворюючи похідні до нових змінних,
одержуємо:
.
Перетворюючи похідні до нових змінних,
одержуємо:
 (2)
(2)
 (3)
(3)
Рівняння (3) називається характеристичним для рівняння (1), а його інтеґрали – характеристиками.
Рівняння (3) – квадратне відносно похідної, тоді:
 (4)
(4)
 називається
дискримінантом
рівняння
(4).
називається
дискримінантом
рівняння
(4).Рівняння (1) називається рівнянням гіперболічного типу, якщо D>0; еліптичного, якщо D<0; параболічного, якщо D=0.
Рівняння
 та
та називаються відповідно першою і другою
канонічними формами гіперболічного
рівняння.
називаються відповідно першою і другою
канонічними формами гіперболічного
рівняння.Рівняння
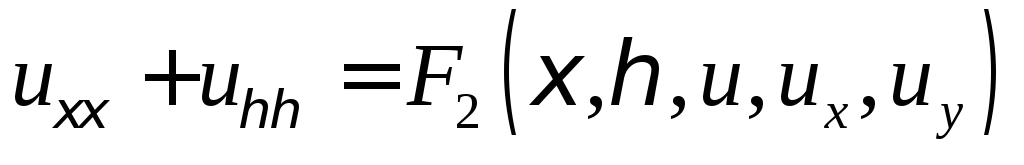 називається канонічною формою
еліптичного рівняння.
називається канонічною формою
еліптичного рівняння.Рівняння
 називається канонічною формою
параболічного рівняння.
називається канонічною формою
параболічного рівняння.
