2.1 Знаходження найкоротшого шляху між двома вершинами графа індексним методом

Серед індексних методів розглянемо метод Форда та його інтерпретацію для машинної реалізації – алгоритм Дейкстри.

Приклад 2.1 Граф G поданий графічно. Необхідно, використовуючи метод Форда, знайти найкоротшу відстань від вершини х₀ до вершини х₇ і довжину цього ланцюга.

Розв'язок. V0=0, V1=…=V₇=...

Розглядаємо всі вершини, суміжні з фіксованою, і вибираємо для розгляду індексу ту, довжина ребра якої має меншу вагу. Це вершина x1.

.

Далі варто розглянути вершину х₂.

.

.

.

.

У результаті одержали, що з вершини х₀ у вершину х₇ існують три найкоротших ланцюги, довжина яких дорівнює 18.

Приклад 2.2 Знайдемо розв'язок попереднього прикладу за допомогою алгоритму Дейкстри.

Рішення. Запишемо вихідні дані у матричному вигляді. Побудуємо матрицю суміжності ваг . Кожний крок відповідає побудові трьох векторів розмірностіn, де n – кількість вершин графа:

А – логічний вектор, елемент а_і=1, якщо вершина х_і розглянута (на початку це вершина відправлення х₀ ) і а_і=0, якщо не розглянута;

В – поточне значення індексів вершин графа, тобто довжина найкоротших шляхів між вершинами х₀ та х_і (на початку елементи вектора В відповідають нульовому рядку матриці Д, оскільки вершина х₀ є початковою, за винятком елемента в₀, який дорівнює 0);

С- містить номери попередніх вершин,тобто с_і – номер вершини, яка стоїть перед і-ю у найкоротшому шляху в і-ту вершину( на початку всі елементи с_і=0, оскільки початкова вершина х₀ і її номер дорівнює 0).

і	0	1	2	3	4	5	6	7	Серед елементів ві вибираємо найменший для нерозглянутих вершин (яким відповідає аі=0). Це елемент в1=4.
Аі	1	0	0	0	0	0	0	0
Ві	0	4	5	9				
Сі	0	0	0	0	0	0	0	0

Таким чином, вершина 1 стає поточною і головною для виконання всіх перетворень даного кроку.

Виконуємо такі перетворення:

а₁=1;

для кожного елемента в_і, який відповідає а_і=0, перевіряємо наявність більш короткого шляху в і-ту вершину з 0-ї через першу, тобто перевіряємо умову в_і<в₁+д_1і . У разі її невиконання замінюємо існуюче значення в_і на в₁+д_1і, а існуюче с_і - на 1.

Для елементів в₂ та в₃ збігаються значення, що порівнюються, тому елементам с₂ та с₃ припишемо два значення 0,1.

і	0	1	2	3	4	5	6	7	Знову серед елементів ві вибираємо найменший для нерозглянутих вершин (яким відповідає аі=0). Це елемент в2=5. Вершина 2 – поточна.
Аі	1	1	0	0	0	0	0	0
Ві	0	4	5	9		6		
Сі	0	0	0,1	0,1	0	1	0	0
2-й єтап									Поточна вершина 5.
Аі	1	1	1	0	0	0	0	0
Ві	0	4	5	9		6	16	
Сі	0	0	0,1	0,1	0	1	2	0
3-й єтап									Поточна вершина 5.
Аі	1	1	1	0	0	1	0	0
Ві	0	4	5	9	14	6	16	21
Сі	0	0	0,1	0,1	5	1	2,5	5
4-й єтап									Поточна вершина 4.
Аі	1	1	1	1	0	1	0	0
Ві	0	4	5	9	14	6	16	21
Сі	0	0	0,1	0,1	5	1	2,5	5
5-й єтап									Поточна вершина 6.
Аі	1	1	1	1	1	1	0	0
Ві	0	4	5	9	14	6	16	21
Сі	0	0	0,1	0,1	5	1	2,5	5
6-й єтап									Для розгляду залишилась одна вершина х7. Її вибір не змінить отриманих результатів, тобто алгоритм перерахунку завершено.
Аі	1	1	1	1	1	1	1	0
Ві	0	4	5	9	14	6	16	18
Сі	0	0	0,1	0,1	5	1	2,5	6

Остання таблиця містить інформацію про довжину найкоротшого шляху від початкової вершини х₀ до будь-якої х_і. Сам шлях можна відтворити за елементами вектора С. Випишемо результат для вершини х₇.

L_min(x₀, x₇)=18,

Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

Завдання №3

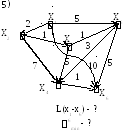
L(x₁-x₅) - ?

⁵_min -?

19)

21)