Завдання №5

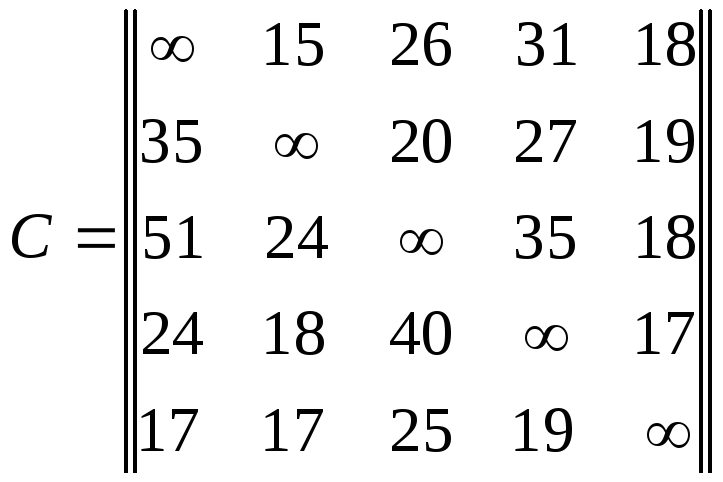
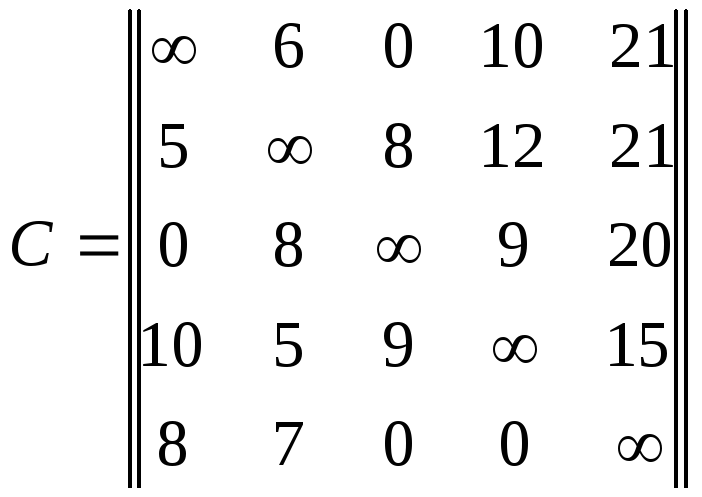
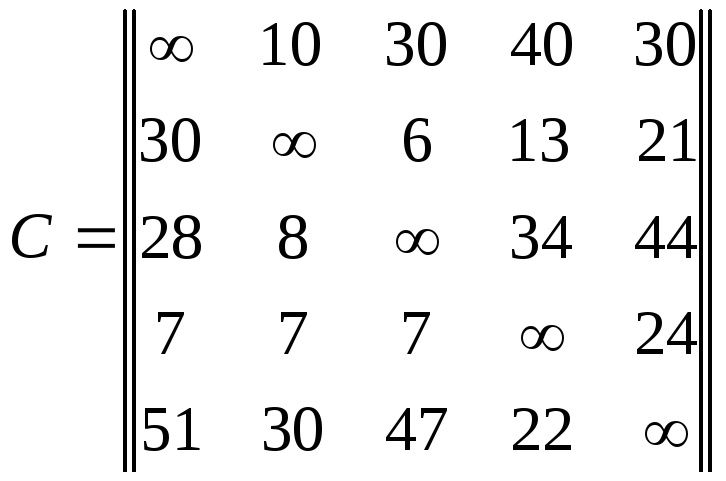
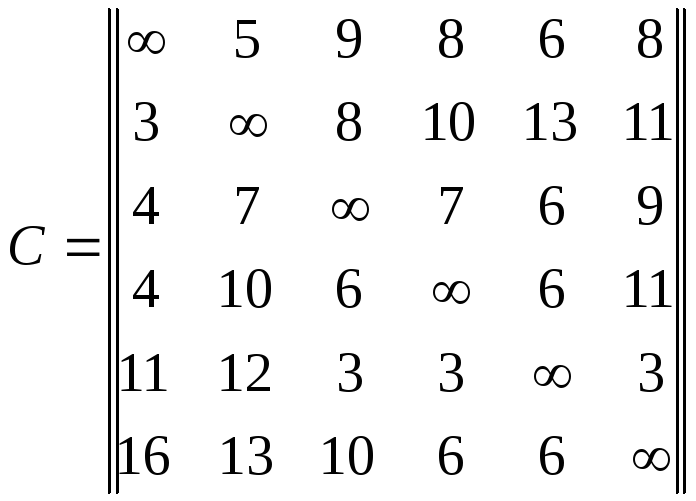
Комівояжерові (торгівельному аґентові) необхідно проїхати через n міст, відвідавши кожне із них тільки раз, і повернутися у вихідне місто. Знайти маршрут комівояжера, що мінімізує сумарні витрати на час проїзду. Час, необхідний комівояжерові для проїзду з кожного i -ого міста в кожне j -те дорівнює cij і зазначено в матриці витрат С. Матриці витрат відповідно до номера варіанту наведено нижче. Розв'язати задачу комівояжера методом гілок і меж.

1. 2. 3.

4. 5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.

2.4 Задача про максимальний потік у транспортній мережі

Транспортною мережею (s/t-мережі) назвемо зв`язний орієнтований граф без петель, у якого є дві особливі вершини s (джерело) та t (стік). Причому:

з вершини s дуги тільки виходять, а у вершину t – тільки заходять; кожній дузі транспортної мережі приписана невід`ємна величина, яка називається пропускною спроможністю дуги і позначається c_ij.

Зафіксуємо деяку вершину s/t-мережі х_к. Для поняття потоку транспортної мережі розглянемо дві множини А-множина всіх вершин s/t-мережі, з яких виходить дуга та заходить у вершину х_к, та В – множина всіх вершин s/t-мережі, які безпосередньо йдують за вершиною х_к. Тоді потоком у s/t-мережі будемо називати невід`ємну величину _ij (для деякої дуги u_ij)=v, якщо виконуються наступні умови:

_ij  c_ij , для будь-якої дуги графа;

Перша умова говорить, що для будь-якої дуги транспортної мережі потік не перевищує пропускну спроможність транспортної мережі, а друга про те, що для будь-якої вершини транспортної мережі сумарний потік, що входить у вершину, дорівнює сумарному потоку, що виходить з вершини, тобто потік неподільний.

Нехай Х – множина всіх вершин s/t-мережі. Розіб`ємо її на дві підмножини Х₁ та Х₂ таким чином, щоб:

Тоді розтином s/t-мережі назвемо множину всіх дуг, що йдують з множини вершин Х₁ до множини вершин Х₂, позначимо (Х₁, Х₂). Величина розтину дорівнює сумі пропускних спроможностей дуг, що створюють розтин, та позначається v(X₁, X₂).

Задача про визначення максимального потоку в транспортній мережі є основною задачею оптимізації на графах. Її розв'язок базується на наступній теоремі Форда-Фалкерсона: максимальний потік у транспортній мережі дорівнює величині найменшого розтину в ній.

Розглянемо розв`язання подібної задачі на прикладі 2.5.

Транспортну мережу задано графічно. Необхідно знайти максимальний потік у s/t-мережі.

Розв`язок. Кожній дузі графа припишемо пару чисел c<sub>ij</sub>, <sub>ij</sub>. На початку в s/t-мережі розподілимо нульовий потік, тобто <sub>ij</sub>=0. Далі для розмітки будь-якої к-ї вершини будемо використовувати позначення к(і<sup>+</sup>, (к)) або к(і<sup>-</sup>, (к)), де і- номер вершини, з якої ми потрапили до вершини к, ‘+’ – по прямій дузі, ‘-‘ – по зворотній дузі, (к) – невід`ємна величина, на яку можна збільшити потік (для прямої дуги) або зменшити (для зворотної дуги). Вершина s завжди має особливу помітку (s⁺, ). Помічати вершини по прямих дугах можна, якщо на цих дугах потік можливо збільшити ( c_ij-_ij >0), а по зворотніх – якщо потік можливо зменшити (_ij >0). Для вершини к(і⁺, (к)) (к)=min((i), c_ik-_ik), а для вершини к(і^-, (к)) (к)=min((i), _ik). Перший крок будь-якого етапу полягає у розставленні поміток вершин мережі, доки або не буде помічено вершину t , тоді переходимо на другий крок, або переконаємося, що вершину t помітити неможливо (задачу розв'язано).

1-й етап. 1-й крок. S(s⁺,). Далі помічаємо вершини суміжні з s. 1(s⁺, min(,10-0) , тобто 1(s⁺,10). Аналогічно 2(s⁺,15), 3(s⁺,15). Тепер вершина s розглянута. Для подальшого розгляду вибираємо будь-яку із суміжних помічених вершин. Наприклад, вершину 3. Помічаємо вершини, суміжні з третьою: 2(3⁺, min(15, 10-0)=10), t(3⁺, min(15,8-0)=8) Помітили вершину t – переходимо до друго кроку 1-го етапу.

2-й крок. За допомогою поміток вершин будуємо ланцюг, який приводить з вершини s до вершини t: t3s. На прямих дугах ланцюга потік збільшуємо на величину (t), а на зворотній – зменшуємо на цю саму величину. На рисунку показано розподіл потоку після виконання першого етапу. Переходимо до другого етапу, який виконуємо аналогічно першому.

2-й етап

S(s^+,)

1(s^+,10) 2(s^+,15) 3(s^+,7)

t(2^+,15) t2s (t)=15

3-й етап

S(s^+,)

1(s^+,10) 3(s^+,7)

4(1^+,7) t(1^+,7) t1s (t)=7

Після 2-го та 3-го етапів розподіл потоку у мережі показано на рисунку.

4-й етап

S(s^+,)

1(s^+,3) 3(s^+,7)

2(3^+,7)

t(2^+,5) t23s (t)=5

5-й етап.

S(s^+,)

1(s^+,3) 3(s^+,2)

4(1^+,3)

t(4^+,3) t41s (t)=3

6-й етап.

S(s^+,)

3(s^+,2)

2(3^+,2)

S(2^-,2)

На 1-му кроці 6-го етапу прийшли до побудови контуру навколо вершиниs, а до вершини t так і не потрапили. Це свідчить про те, що потік у мережі збільшити неможливо. Будуємо розтин мережі: віднесемо до множини Х₁ усі вершини, що помічені на 6-му кроці, а до множини Х₂ – ті, що не помічені. Х₁={s, 2, 3}, X₂={1, 4, t}, (X₁, X₂)={u_s1, u_2t, u_3t}, v(X₁, X₂)=c_s1+c_2t+c_3t=10+20+8=38. Перевірка: якщо просумувати всі значення (t): 8+15+7+5+3=38, то це число збігається з величиною побудованого розтину.

Візьмемо вихідний граф і лінією відокремимо множину вершин Х₁ від множини вершин Х₂. Ті дуги, які перетинають отриману лінію і мають напрямок від вершин з множини Х₁ до вершин з множини Х₂ і є дугами розтину.

На рисунку також показано результуючий розподіл потоку у мережі.