Розділ 4. Похідна та її застосування. Інтеграл

Приклад 4.1. Знайти рівняння прямої, яка проходить через точку з координатами 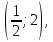дотикається графіка функціїі перетинає у двох різних точках графік функції

Позначимо через х=х₀,у=у₀ координати точки, в якій пряма дотикається графіка функції .

Оскільки то її рівняння можна записати у вигляді:

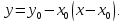
За умовою , точка належить цій прямій, а точка (х₀;у₀) – графіку функції . Звідси:

Отже, дотичні до графіка функції в точках

Мають рівняння

Залишилося розв’язати дві системи:

Відповідь:.

Приклад 4.2. Довести, що для функції виконується нерівність

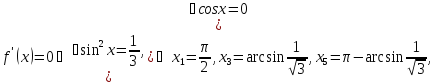
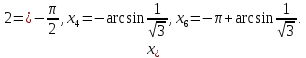
Приклад 4.3. знайти найменшу відстань від точки М(0;-2) до кривої

Нехай точка N(х;у) належить графіку функції

Знайдемо найменше значення функції на множині

Оскільки 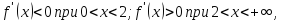то найменше значення функціїна множинідорівнює.

Відповідь:

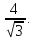
Приклад 4.4. Точки М і N лежать на параболах у=х², у=-(х-6)² відповідно. Знайти найменше значення М N.

Оскільки параболи симетричні відносно точки С(3;0), то і найближчі точки цих парабол М і N відповідно теж симетричні відносно точки С.

Тоді М N=МС+С N=2МС

Відповідь:

Приклад 4.5. Знайти сторону рівностороннього трикутника найбільшої площі, дві вершини якого лежать на прямій а третя вершина належить фігурі, обмеженій лініями у=х²-2х, у=2х-1.

Використовуючи геометричні образи заданих рівнянь, покажіть, що в силу опуклості тієї частини границі заданої фігури, яка співпадає з частиною параболи у=х²-2х, найвіддаленішою від прямої точкою заданої фігури є точка А(х₀;у₀), у якій дотична до параболи у=х²-2х паралельна прямій . Відстань d між цією дотичною і прямою у=2х-1 і є висотою трикутника максимальної площі.

Відповідь: .

Приклад 4.6. Знайти всі точки прямої, сума відстаней від кожної з яких до точок A(0), B(5), C(7), D(10) буде найменшою.

Нехай М(х) – шукана точка. Необхідно знайти всі значення хєR при яких функція

досягає мінімуму.

Відповідь: хє[5;7].

Приклад 4.7. Знайти всі значення параметра а, при кожному з яких функція

має додатну точку максимуму.

Показати, що задача зводиться до того, щоб знайти всі а, при кожному з яких менший корінь, а отже, і обидва корені рівняння додатні. За теоремою Вієта:

Відповідь:

Приклад 4.8. Знайти всі значення параметра а, при кожному з яких функція

зростає і не має критичних точок для хєR.

Якщо для всіх хєR виконується нерівність у’(х)>0, то функція у(х) не має критичних точок і зростає.

При х=0 маємо

Якщо і для всіх хєR маємо:

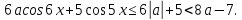
Відповідь: ає(6;+

Приклад 4.9. Знайти всі значення параметра а, при кожному з яких функція

Зростає для всіх значень хєR і при цьому не має критичних точок.

Задачу можна перефразувати так: знайти всі значення параметра а, при кожному з яких для довільного хєR виконується нерівність

або найменше значення функції на відрізку [-1;1] додатне:

Найменше значення m функції g(t) на відрізку [-1;1] дорівнює:

Відповідь:

Приклад 4.10. Знайти всі значення параметра а, при кожному з яких функція

Має на відрізку не менше двох критичних точок.

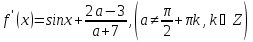Задача зводиться (в силу періодичності y=sinx) до знаходження всіх значень a, при кожному з яких рівняння має розв’язки на відрізку

На цьому відрізку sinx<0, причому .

З системи

Відповідь:

Приклад 4.11. Знайти всі значення параметра а, при кожному з яких хорда параболи дотикається до кривої у точці з абсцисою х=2 і ділиться цією точкою навпіл.

Отже у=х-3 – рівняння дотичної, проведеної до графіка функції з абсцисою у точці х=2. Нехай х₁ і х₂ – абсциси кінців хорди (розв’язки рівняння ). Якщо корені існують, то їх сума дорівнює .

Отже, задача звелася до розв’язання змішаної системи:

Відповідь: а=1.

Приклад 4.12. Знайти значення параметрів p і m, при яких мінімум функції

не менше 1 і досягається при х=1.

+.

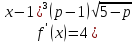Для того, щоб х=1 була точкою мінімуму, необхідно виконання умови

Оскільки (2)

Якщо х=1 точка мінімуму, то при наприклад:

Із (1)-(3) випливає, що .

Функція

Має точку мінімуму х=1 і цей мінімум не менше 1, якщо:

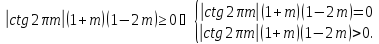
Відповідь:

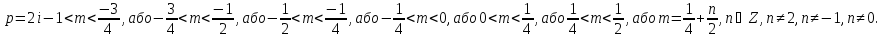
Приклад 4.13. Знайти всі значення параметра а, при кожному з яких площа фігури яка належить півплощині х≥0, і обмежена прямими у=1, у=2 і кривими буде найбільшою. Знайти цю площу.

Розв’язуючи відповідні системи рівнянь, знаходимо абсциси координат точок A, B, C, D:

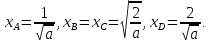
Тоді площа криволінійної трапеції

Функція в області vмонотонно спадає.

Отже,

Відповідь: