
- •Завдання для самостійної роботи.
- •Завдання з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
- •Завдання з теми «Диференціальне числення функції однієї змінної».
- •Завдання з теми «Невизначений та визначений інтеграли».
- •Завдання з теми «Диференціальні рівняння та системи».
- •Завдання з теми «Ряди».
- •Зразки виконання завдань.
- •Розв’язання завдань з теми «Лінійна та векторна алгебри. Елементи аналітичної геометрії».
- •Розв’язання завдань з теми «Диференціальне числення функції однієї змінної».
- •Розв’язання завдань з теми «Невизначений та визначений інтеграли».
- •Розв’язання завдань з теми «Диференціальні рівняння та системи».
- •Розв’язання завдань з теми «Ряди».
- •Література
Розв’язання завдань з теми «Диференціальне числення функції однієї змінної».
Завдання 1.
Знайти границі функцій, не користуючись правилом Лопіталя.
а)
 .
.
Розв’язання.
При
 чисельник і знаменник дробу прямують
до нескінченності. Маємо невизначеність
чисельник і знаменник дробу прямують
до нескінченності. Маємо невизначеність .
Щоб розкрити її, поділимо чисельник і
знаменник дробу на найвищу степінь
.
Щоб розкрити її, поділимо чисельник і
знаменник дробу на найвищу степінь ,
що зустрічається у членів дробу, тобто
на
,
що зустрічається у членів дробу, тобто
на :
:

 .
.
Відповідь. 0.
б)
 .
.
Розв’язання.
При
 чисельник і знаменник дробу прямують
до нуля. Отже, маємо невизначеність
чисельник і знаменник дробу прямують
до нуля. Отже, маємо невизначеність .
Для її розкриття позбавимось
ірраціональності в чисельнику: помножимо
чисельник і знаменник на
.
Для її розкриття позбавимось
ірраціональності в чисельнику: помножимо
чисельник і знаменник на і скористаємось формулою
і скористаємось формулою .
Знаменник розкладемо на множники за
формулою
.
Знаменник розкладемо на множники за
формулою ,
де
,
де і
і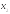 - корені квадратного тричлена. Знайдемо
їх:
- корені квадратного тричлена. Знайдемо
їх:
 ;
;
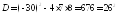 ;
; ;
;
 ,
,
 .
.
Отже,
 .
Таким чином,
.
Таким чином,


 .
.
Відповідь.
 .
.
в)
 .
.
Розв’язання.
При обчисленні цієї границі маємо
невизначеність
 .
Розкриваючи її, розкладемо знаменник
на множники за формулою
.
Розкриваючи її, розкладемо знаменник
на множники за формулою :
: і перепишемо границю так:
і перепишемо границю так:

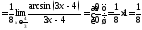 .
.
До останньої границі був застосований наслідок з першої важливої границі.
Відповідь.
 .
.
г)
 .
.
Розв’язання.
При
 вираз у дужках прямує до 1, а показник
степеня до
вираз у дужках прямує до 1, а показник
степеня до .
Маємо невизначеність
.
Маємо невизначеність .
Щоб розкрити її, перетворимо границю
так:
.
Щоб розкрити її, перетворимо границю
так:

 .
.
Відповідь.
 .
.
Завдання 2.
Знайти похідні функцій.
а)
 .
.
Розв’язання.
За правилом диференціювання складеної
функції
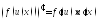 маємо
маємо


 .
.
При цьому
використовувались наступні формули
диференціювання:
 ,
,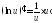 ,
, ,
, ,
, .
.
Відповідь.
 .
.
б)
 .
.
Розв’язання.
Це рівняння задає функцію
 неявно. Щоб знайти похідну, продиференціюємо
обидві його частини, пам’ятаючи, що
неявно. Щоб знайти похідну, продиференціюємо
обидві його частини, пам’ятаючи, що є функція змінної
є функція змінної :
:
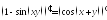 ,
,
 ,
,
 .
.
Отримане
рівняння розв’яжемо відносно
 :
:
 ,
,
 ,
,
 ,
,
 .
.
Відповідь.
 .
.
в)
 .
.
Розв’язання.
Для обчислення похідної такої функції
(так званої степенево-показникової)
використаємо логарифмічне диференціювання:
прологарифмуємо обидві частини рівності
 .
Отримаємо
.
Отримаємо
 .
.
Тепер,
продиференціювавши ліву і праву частини
останньої рівності, враховуючи, що
 ,
знаходимо
,
знаходимо
 ,
,
 ,
,
 .
.
Звідки
 або
або
 .
.
Відповідь.
 .
.
г)

 ,
,
Розв’язання.
Функція задана параметрично. Її похідна
обчислюється за формулою
 .
.
Знайдемо
 та
та
 .
Отже,
.
Отже,
 .
.
Друга
похідна функції, заданої параметрично,
знаходиться за формулою
 .
Диференціюємо отриману похідну за
змінною
.
Диференціюємо отриману похідну за
змінною :
:
 .
.
За допомогою наведеної вище формули дістанемо
 .
.
Відповідь.
 ;
; .
.
Завдання 3.
Визначити
диференціал
 функції
функції ,
якщо
,
якщо .
.
Розв’язання.
Диференціал функції
 обчислюється за формулою
обчислюється за формулою .
.

 .
.
 .
.
Відповідь.
 .
.
Завдання 4.
Методами
диференціального числення дослідити
функцію
 і за результатами дослідження побудувати
її графік.
і за результатами дослідження побудувати
її графік.
Розв’язання.
Задана функція дробово-раціональна.
Отже, вона визначена при всіх
 ,
крім точок
,
крім точок і
і .
Дослідимо поведінку функції в їх околі.
Для цього обчислимо односторонні границі
при
.
Дослідимо поведінку функції в їх околі.
Для цього обчислимо односторонні границі
при і при
і при :
:
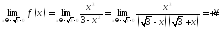 ;
;
 ;
;
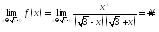 ;
;
 .
.
Знайдені
границі говорять про те, що обидві точки
є точками розриву другого роду і
визначають вертикальні асимптоти,
рівняння яких
 і
і .
.
На
інтервалах
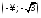 ,
, ,
, функція неперервна.
функція неперервна.
Знайдемо точки перетину графіка з осями координат:
а)
з віссю
 :
якщо
:
якщо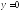 ,
то
,
то ;
;
б)
з віссю
 :
якщо
:
якщо ,
то
,
то .
.
Отже,
графік функції перетинає координатні
осі в точці
 ,
тобто проходить через початок координат.
,
тобто проходить через початок координат.
Знайдемо
інтервали знакосталості функції.
Розв’яжемо нерівність
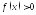 :
: :
:

+
--


Таким
чином,
 на інтервалах
на інтервалах і
і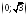 ;
; на інтервалах
на інтервалах і
і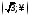 .
На інтервалах
.
На інтервалах![]() і
і![]() графік функції розташований вище осі
графік функції розташований вище осі ,
а на інтервалах
,
а на інтервалах![]() і
і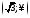 нижче осі
нижче осі .
.
Функція непарна, оскільки
 ,
тому її графік симетричний відносно
початку координат. Подальше дослідження
можна проводити для
,
тому її графік симетричний відносно
початку координат. Подальше дослідження
можна проводити для
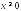 .
.
З’ясуємо
поведінку функції при
 :
:
 .
Отже, горизонтальна асимптота відсутня.
.
Отже, горизонтальна асимптота відсутня.
Похилу
асимптоту будемо шукати у вигляді
 :
:
 ,
,
 Отже,
Отже,
 - рівняння похилої асимптоти.
- рівняння похилої асимптоти.
Дослідимо функцію на монотонність та екстремум:

 .
.
З рівняння
 знайдемо критичні точки першого роду:
знайдемо критичні точки першого роду:
 ⇔
⇔ ⇒
⇒
Враховуючи непарність функції, встановимо знак першої похідної на інтервалах
 ,
, ,
,
 .
.

0

3
Таким
чином, функція зростає на інтервалах
 ,
, ;
спадає на інтервалі
;
спадає на інтервалі .
В
точці
.
В
точці
 функція має максимум, рівний
функція має максимум, рівний .
.
Знайдемо інтервали опуклості графіка функції і точки перегину:


 .
.
Розв’язуючи рівняння
 ,
знайдемо критичні точки другого роду:
,
знайдемо критичні точки другого роду:
 ⇔
⇔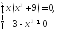 ⇒
⇒
Знак другої похідної встановимо на інтервалах
 ,
, .
.

Таким
чином, на інтервалі
![]() графік функції вгнутий, а на інтервалі
графік функції вгнутий, а на інтервалі![]() - опуклий.
- опуклий.
Враховуючи
непарну симетрію кривої, точка
 є точкою перегину. Точка
є точкою перегину. Точка - точка розриву і не може бути точкою
перегину.
- точка розриву і не може бути точкою
перегину.
За
результатами дослідження будуємо графік
функції для
 .
Частина графіка для
.
Частина графіка для відображається за принципом непарної
функції (поворотом на
відображається за принципом непарної
функції (поворотом на відносно початку координат).
відносно початку координат).



