2. Розв’язання завдань з теми «Невизначений та визначений інтеграли».

Завдання 1.

Знайти невизначені інтеграли. У завданнях а), б), в), г) результати перевірити диференціюванням.

а) .

Розв’язання. Нехай , тодіабо. Отже, маємо:

.

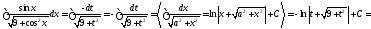
Перевірка.

.

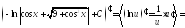
Відповідь. .

б) .

Розв’язання. Оскільки , то зробимо заміну. Тоді, і

.

Перевірка.

.

Відповідь. .

в) .

Розв’язання. До заданого інтеграла застосуємо метод інтегрування частинами, скориставшись формулою . Покладемо, а. Тоді, а. За формулою інтегрування частинами маємо:

.

Перевірка.

.

Відповідь. .

г) .

Розв’язання. Підінтегральний раціональний дріб неправильний. Виділимо з нього цілу частину діленням чисельника на знаменник:

Маємо . Розкладемо тепер дрібна елементарні:

1. знайдемо корені квадратного тричлена :

;

; ,.

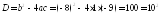2. за формулою маємо

.

3. . Знайдемо невизначені коефіцієнти і:. З рівності дробів з однаковими знаменниками маємо.

Якщо , то,.

Якщо , то,.

Отже, , а підінтегральний дріб матиме вигляд. Інтегруємо цей вираз

.

Перевірка.

.

Відповідь. .

д) .

Розв’язання. Перетворимо підкореневий вираз:

.

Нехай , тоді,, і заданий інтеграл матиме вигляд:

. Обчислимо кожний із отриманих інтегралів окремо.

. Скористаємось формулою .

.

.

Таким чином, , де.

Відповідь. .

е) .

Розв’язання. Перетворимо добуток тригонометричних функцій у суму за формулою 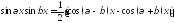, а потім проінтегруємо одержаний вираз за відомими формулами з таблиці інтегралів і з використанням властивостей інтегралів:

.

Відповідь. .

є) .

Розв’язання. До поданого інтеграла застосуємо підстановку . Тоді, а;,. Одержимо

.

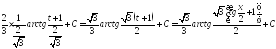Відповідь. .

ж) .

Розв’язання. Зведемо заданий інтеграл до інтеграла від раціональної функції за допомогою підстановки . Тоді, а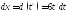. Дістанемо

.

Повертаючись до змінної , одержуємо

.

Відповідь. .

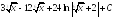Завдання 2.

Знайти площу фігури, обмеженої параболою і прямою.

Розв’язання. Побудуємо фігуру, площу якої треба обчислити. Для цього знайдемо координати вершини параболи:

; .

Таким чином, .

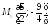Вісь парабола перетинає в точці, а вісьв точкахі, координати яких знайдено з рівняння.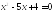

Координати точок перетину параболи і прямої знайдемо, розв’язавши систему рівнянь:

; ;;;.

Одержали ,. Абсциси цих точок є границями інтегрування при обчисленні площі побудованої фігури. Таким чином,

.

Відповідь. .

Завдання 3.

Знайти об’єм тіла обертання відносно горизонтальної асимптоти для кривої ,.

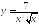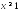Розв’язання. Для кривої горизонтальною асимптотою є вісь, оскільки. Об’єм тіла, утвореного обертанням кривоїнавколо осі, обчислюється за формулою

,

де за умовою задачі ,,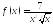. Отже, маємо

.

Відповідь. .

Завдання 4.

Знайти довжину дуги кривої між точками її перетину з віссю.

Розв’язання. Знайдемо абсциси точок перетину даної кривої з віссю . Для цього розв’яжемо рівняння:

: ,.

Довжину дуги кривої між точками з абсцисами іобчислимо за формулою. Складемо вираз.

.

.

. Знайдемо невизначений інтеграл

. Отже, .

Відповідь. .

2. Розв’язання завдань з теми «Диференціальні рівняння та системи».

Завдання 1.

а) Знайти загальний розв’язок диференціального рівняння

.

Розв’язання. Подане рівняння – це диференціальне рівняння першого порядку з відокремлюваними змінними. Поділимо обидві його частини на добуток :

.

Одержимо рівняння

,

яке проінтегруємо

.

Знайдемо окремо кожний інтеграл:

1. ;

2. .

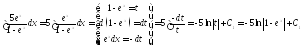Отже, маємо

,

.

Праву частину отриманого виразу зручно подати як натуральний логарифм сталої , тобто.

Таким чином,

або

,

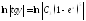звідки

,

а - це загальний розв’язок заданого рівняння.

Відповідь. .

б) Знайти загальний розв’язок або загальний інтеграл диференціального рівняння

.

Розв’язання. Перепишемо задане рівняння у вигляді

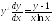
і помножимо його на :

.

В отриманому рівнянні відокремимо змінні. Для цього поділимо обидві частини на :

.

Одержимо

.

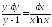Тепер проінтегруємо:

.

Знайдемо кожний інтеграл окремо:

1. 

;

2. .

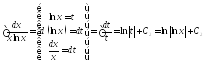Остаточно маємо:

або , де,, і

Отримали загальний інтеграл заданого диференціального рівняння.

Відповідь. ,.

Завдання 2.

Знайти загальний інтеграл диференціального рівняння

.

Розв’язання. Перетворимо задане рівняння

;

.

Отримали рівняння вигляду . Це означає, що задане диференціальне рівняння однорідне (нелінійне). Рзвя’жемо його за допомогою підстановки . Тоді,.

Отже, маємо

,

,

.

В отриманому рівнянні відокремимо змінні

і проінтегруємо

.

Знайдемо окремо кожний інтеграл:

1. 

, ;

2. , .

Таким чином,

,

, де ,

,

, .

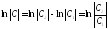- загальний інтеграл заданого рівняння.

Відповідь. .

Завдання 3.

Знайти розв’язок задачі Коші для диференціального рівняння першого порядку

, .

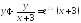Розв’язання. За умовою маємо лінійне рівняння вигляду , де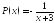,. Розв’яжемо його за допомогою підстановки, де,- невідомі функції змінної, причому одна з них довільна. Похідна цієї функції дорівнює. Підставимо цей вираз і виразу задане рівняння:

,

.

Знайдемо функцію такою, щоб

, тоді .

Розв’яжемо ці два рівняння.

1. . Перепишемо його у вигляді і відокремимо у ньому змінні:

.

Проінтегруємо це рівняння

,

і одержуємо . Довільну сталу ми опустили, оскільки досить отримати частинний розв’язок рівняння .

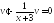Підставимо тепер вираз у рівнянняі розв’яжемо його:

2. , .

Це рівняння також є рівнянням з відокремлюваними змінними:

,

,

.

Підставимо знайдені вирази іу формулу. Отримаємо загальний розв’язок заданого диференціального рівняння

.

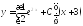Виділимо з цього розв’язку частинний, що задовольняє початкову умову , тобто розв’яжемо задачу Коші:

,

.

Таким чином, розв’язок задачі Коші

.

Відповідь. .

Завдання 4.

Знайти загальний розв’язок або загальний інтеграл диференціального рівняння

.

Розв’язання. Задане рівняння не містить явно змінну , тобто це рівняння вигляду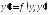. Покладемо в ньому, тоді. Отримаємо диференціальне рівняння першого порядку

або

.

Звідки або.

Якщо , то. Ця функція є розв’язком заданого рівняння, оскільки перетворює його на тотожність (,).

Розв’яжемо рівняння , яке є рівнянням з відокремлюваними змінними:

,

,

, ,

,

,

,

.

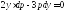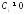Виконуючи обернену заміну , отримаємо рівняння

,

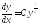в якому відокремимо змінні та проінтегруємо :

,

,

,

,

,

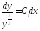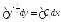або .

Отримали загальний розв’язок даного рівняння.

Відповідь. ,.

Завдання 5.

Знайти загальний розв’язок диференціального рівняння

.

Розв’язання. Задане диференціальне рівняння неоднорідне другого порядку зі сталими коефіцієнтами і правою частиною спеціального вигляду. Йому відповідає однорідне рівняння

.

Його характеристичне рівняння

має корені: ,().

Оскільки корені характеристичного рівняння комплексні, то загальний розв’язок однорідного рівняння матиме вигляд

,

тобто

.

Частинний розв’язок неоднорідного рівняння будемо шукати в залежності від вигляду правої частини даного рівняння, тобто

,

де 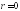, оскільки серед коренів характеристичного рівняння нема рівних нулю.

.

Знайдемо і:

, .

Підставимо іу дане рівняння:

,

.

Порівняємо коефіцієнти при однакових степенях :

; ,.

Підставимо знайдені значення коефіцієнтів у формулу частинного розв’язку:

.

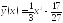Загальний розв’язок лінійного неоднорідного рівняння має вигляд

,

а заданого рівняння

.

Відповідь. .

Завдання 6.

Знайти загальний розв’язок системи лінійних диференціальних рівнянь зі сталими коефіцієнтами

методом характеристичного рівняння.

Розв’язання. Для заданої системи лінійних диференціальних рівнянь запишемо характеристичне рівняння

і розв’яжемо його

,

,

,

, .

Частинні розв’язки системи будемо шукати у вигляді:

, ;,.

Щоб знайти і, складемо систему лінійних алгебраїчних рівнянь

.

При маємо систему

.

Система має нескінченну множину розв’язків. Знайдемо один з них. Нехай , тоді, і частинні розв’язки системи будуть:

, .

При маємо систему

.

В цьому випадку покладемо , тоді, і частинні розв’язки матимуть вигляд

, .

Загальний розв’язок системи знайдемо за формулою

.

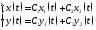Отже, маємо

.

Відповідь. .

Завдання 7.

Розв’язати методом виключення невідомих систему диференціальних рівнянь, що задовольняють нульовим початковим умовам

.

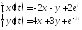Розв’язання. Продиференціюємо перше рівняння системи

,

в яке замість 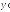підставимо вираз для нього з другого рівняння заданої системи:

.

В цьому рівнянні замінимо виразом, який знайдемо з першого рівняння системи:

. (1)

Отримаємо

або

. (2)

Це диференціальне рівняння другого порядку зі сталими коефіцієнтами. Відповідне однорідне рівняння має вигляд

. (3)

Його характеристичне рівняння

має корені ,- дійсні та різні. Отже, загальний розв’язок однорідного рівняння (3) має вигляд

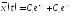. (4)

Частинний розв’язок неоднорідного рівняння (2) будемо шукати у відповідності з правою частиною цього рівняння у вигляді

. (5)

Знайдемо першу та другу похідні функції :

, (6)

. (7)

Підставимо в рівняння (2) замість ,,відповідні вирази з формул (5), (6), (7):

або

.

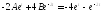Порівнюючи коефіцієнти при і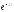, дістанемо систему рівнянь:

,

з якої ,.

Таким чином, частинний розв’язок неоднорідного рівняння (2) такий

,

а загальний розв’язок має вигляд

. (8)

Знайдемо :

.

Підставимо вирази для іу формулу (1):

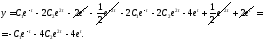(9)

Таким чином, маємо загальний розв’язок заданої системи:

Тепер розв’яжемо задачу Коші, використовуючи знайдені розв’язки і нульові початкові умови. Побудуємо систему рівнянь:

або

.

Підставляємо знайдені значення довільних сталих в рівності (8) і (9) і одержуємо розв’язок задачі Коші у вигляді:

.

Відповідь. .