1. Найдём вероятности :

Зная, что , имеем:+=1 - (0,2+0,1+0,2)=0,5;

;

;

; ;

.

2. Дисперсию найдём по формуле:

Ответ: 1. ;.

2.

Задача 7­­­-5. Плотность распределения непрерывной случайной величины Х имеет вид:

Найти:

а) параметр ;

б) функцию распределения ;

в) вероятность попадания случайной величины Х в интервал (4;6);

г) математическое ожидание M (X) и дисперсию D (X);

д) построить графики функций f(x) и F(x).

Решение:

а) Найдём параметр .

Из условия, что и значения данной случайной величины заключены в промежутке, то

, откуда ;

б) Найдём функцию распределения .

Из свойства функции плотности имеем: .

Рассмотрим три интервала.

При .

.

При .

.

При .

Таким образом,

в) Найдём вероятность попадания случайной величиныв интервал

(4; 6).

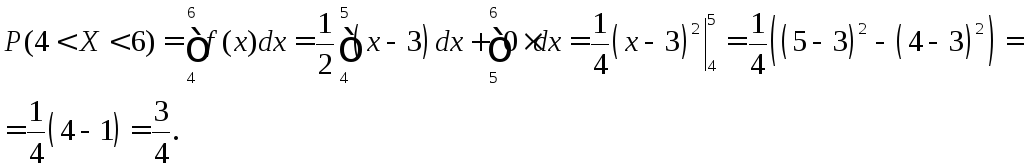
г) Найдём математическое ожидание M (X) и дисперсию D (X):

д) построим графики функций f(x) и F(x).

Ответ: а). б)

в) г)

Задача 8-6. Случайная величина имеет биномиальное распределение. Найти вероятность, если математическое ожидание, а дисперсия.

Решение:

Для биномиального закона распределения имеем: ;.

Зная из условия, что математическое ожидание , а дисперсия

. Найдем из системы уравнений: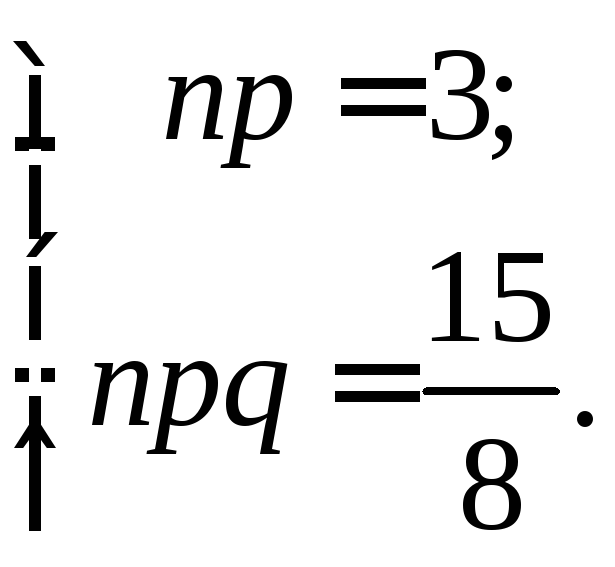

Делим одно уравнение на другое, получаем:

; а ; тогда.

Вероятность: .

По формуле Бернулли: .

Таким образом, получим:

Окончательно, имеем:

Ответ:

Задача 7. Случайные величины имеют равномерное, показательное и нормальное распределения соответственно. Найти вероятности, если у этих случайных величин математические ожидания и средние квадратические отклонения равны 3.

Решение:

1. Закон равномерного распределения имеет вид:

Найдём параметры ииз условия:

; .

Зная, что математические ожидания и средние квадратические отклонения равны 3, найдем :

Решим систему уравнений: , получим:

Так как предполагается, что , то.

Определяем искомую вероятность:

2. Показательное распределение имеет вид:

Для показательного распределения: ; . Тогда.

3. Вероятность попадания в заданный интервал нормального распределённой случайной величины определяется как:

.

Здесь . Тогда

где функция Лапласа определяется по таблицам.

Ответ:

1.

2.

3.

Задача 10-9. Выборка Х объемом измерений задана таблицей:

	5	13			19	10	3

результаты измерений;частоты, с которыми встречаются значения;.

а) Построить полигон относительных частот ;

б) вычислить среднее выборочное , выборочную дисперсиюи среднее квадратическое отклонение;

в) по критерию проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости.

Решение:

а) Построить полигон относительных частот .

	5	13			19	10	3

Вычисляя относительные частоты: , получаем:

	0,6	1,2	1,8	2,4	3	3,6	4,2
			25	25
	0,05	0,13	0,25	0,25	0,19	0,10	0,03

Построим полигон относительных частот.