nст = FFкр = 1710,4800 = 2,14.

Перевіряємо умову стійкості (5.7). За табл. 5.2. визначаємо відповідний гнучкості λ=100,33 коефіцієнт

ϕ = 0,6 − 0,6 10−0,52 (100,33 −100)= 0,5974,

допустиме напруження на стійкість [σст] = φ[σ–] = 0,5974·160=95,58 МПа і перевіряємо умову стійкості (5.7)

	800 103	2
σ =		=91,45·10 Н/м =91,45 МПа<95,58 МПа
	0,75 0,1082

на ε = 95,58 −91,45 100 =4,32% <5%, 95,58

що допустимо.

Приклад 5.2. Підібрати номер двотавра для сталевої стійки (рис. 5.3), якщо [σ–]=160 МПа.

При доборі перерізів стиснутих стержнів із прокатних профілів більш зручно прагнути до виконання умови стійкості, а не збігу коефіцієнтів ϕn і ϕn′.

Задаємо ϕ 1 = 0,6 і обчислюємо площу поперечного перерізу за формулою

(5.8)

	Aбр=	1000 103	=1,042 10−2 м2 =104,2 см2.
		0,6 160 106

За сортаментом знаходимо двотавр № 50 з найближчою площею

A=100 см2 і imin = iy =3,23 см.

Далі обчислюємо за формулою (5.2) гнучкість стійки

λ= 0,03230,5 8 =123,84

іза табл. 5.2 визначаємо відповідне їй значення коефіцієнта

ϕ1′ = 0,45 − 0,45 −0,40 (123,84 −120)= 0,4308; 10

допустиме напруження на стійкість

[σст] = φ[σ ]=0,4308·160=68,93 Мпа і перевіряємо умову стійкості (5.7)

137

	F		1000 103	6	2
σ =		=	100 10−4 =100·10		н/м =100 МПа>[ σст]
	A
	бр

на ε =100 −68,93 100 =45,07% >5%, тому спробуємо взяти двотавр № 55: 68,93

Aбр = 118 см2, imin = 3,39 см.

Для цього двотавра

λ= 0,03390,5 8 =117,99; φ2 = 0,4641; [σст]=0,4641·160=74,26 МПа,

σ=1000 10−3 =84,75·106 Н/м2 =84,75 МПа >74,26 МПа на 14,13% . 118 10 4

Тому спробуємо двотавр № 60:

Aбр=138 см2, imin = 3,54 см, Jmin = 1725 см4.

Для цього двотавра обчислюємо

λ= 0,03540,5 8 =112,99; φ3 = 0,4991, [σст] = 0,4991·160 = 79,86 Мпа і перевіряємо умову стійкості (5.7)

=1000 103 = 6 2 σ − 72,46·10 Н/м =72,46 МПа<[ σст]=79,86 Мпа

138 10 4

на ε	=	79,86 −72,46	100 =9,26%,
		79,86

тобто стійка недовантажена на 9,26%, але зменшити це недовантаження неможливо, тому що найближчий менший номер двотавра, як було встановлено раніше, недостатній.

Обчислимо коефіцієнт запасу стійкості nст. Оскільки λ=112,99>λгр=100, то для визначення критичної сили використовуємо формулу Ейлера (5.4)

Fкр= 3,142 2 105 1062 1725 1−8 = 2126 103 Н = 2126кН, (0,5 8)

nст= FFкр = 10002126 = 2,13.

138

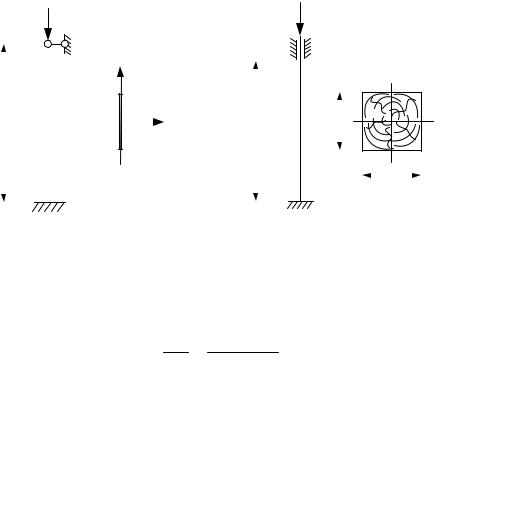
Приклад 5.3. Визначити номер двотавра стиснутої сталевої стійки (рис. 5.4), якщо коефіцієнт запасу стійкості її nст =2,7.

l = 2м

l = 4м

Рис. 5.4

Рис. 5.5

Скористаємося для визначення критичної сили формулою Ейлера (5.4). При цьому умова стійкості (5.1) приймає вигляд

F≤ Fкр = π2E Jmin . nст (νl)2nст

Звідси знайдемо необхідний мінімальний момент інерції поперечного перерізу стійки

Jmin ≥

F n (νl)2

160 103 2,7(0,7 2)2

= 4,294 10

−7

= 42,94 см

4

.

ст

=

3,142 2 1011

π2 E

За сортаментом знаходимо двотавр № 14:

( J

min

= J

y

= 41,9 см4 , i

= i

y

=1,55см,

А =17,4 см2 )

min

бр

і обчислюємо гнучкість стійки

	λ =	νl	=		0,7 2	=90,32 <λ	гp	=100 ,
		i		1,55 102
		min

тому формулу Ейлера застосовувати не можна. Треба виконати перерахунок за формулою Ясинського:

[F] =	Fкр	=	Aбр	(a −bλ) =	17,4 10−4	( 310 −1,14 90,32 ) 10	6	=133,42кН< F
	n		n		2,7
	ст		ст

на ε =160 −133,42 100% =16,6% >5%, що недопустимо. 160

139

Спробуємо наступний найближчий двотавр № 16: (Aбр=20,2 см2, Jmin =Jy= =58,6 см4, imin =iy =1,70 см).

Для цього двотавра маємо

		λ=	νl		=	0,7 2		=82,35<λгр=100,
			i
					1,7 10−2
			min
тому [F] =	A	(a −bλ) =		20,2 10−4			(310 −1,14 82,35) 10		6	=161,69 кН > F
	n				2,7
	ст

на ε=1.06 % < 5 %, що допустимо. Приймаємо двотавр № 16.

Приклад 5.4. Перевірити стійкість дерев’яної стійки (рис. 5.5), якщо допустиме напруження на стискання [σ–]=10 МПа.

Через те що коефіцієнт запасу стійкості не заданий, розрахунок виконуємо за коефіцієнтом φ – зниження основних допустимих напружень. Визначаємо геометричні характеристики поперечного перерізу стійки і її гнучкість:

A

= a2 ; J

min

= a4

; i

=

Jmin

=

a

=

12

= 3,46 см.

бр

12

min

Aбр

12

12

λ =

νl

=

0,5 4

= 58 .

i

3,46 10−2

min

За табл. 5.2 знаходимо φ=0,73 і обчислюємо допустиме напруження на стійкість [σст]=φ[σ–]=0,73·10=7,3 МПа.

Тепер перевіряємо, чи виконується умова стійкості (5.7):

σ =

F

=

100 103

= 6,94 10

6

H/м

2

= 6,94MПа <[σ

ст

] = 7,3MПа

A

122

10−4

бр

на ε = 7,3 −6,94 100% = 4,93% . 7,3

Стійка недовантажена на 4,93% <5%, що допустимо.

Визначимо коефіцієнт запасу стійкості. Оскільки λ = 58 < λгр = 110 (див. табл. 5.1), то

Fкр = Aбр(a −bλ) = 0,122 (29,3 −0,194 58) 106 = 2,599 105 Н = 259,9кН,

nст = FFкр = 259,9100 ≈ 2,6 ,

140

тобто близький до нормативного.

Приклад 5.5. Визначити допустиме значення осьової сили F для центрально стиснутого стержня з сталі Ст.5 (рис. 5.6), якщо nст = 4, а Е= 2,1·105 МПа.

У даному випадку закріплення кінців стержня в головних площинах інерції є різними, тому втрата стійкості його відбудеться відносно тієї головної осі, відносно якої гнучкість буде більшою.

Визначимо геометричні характеристики перерізу відносно головних осей інерції (рис. 5.6, а).

l = 2.5м

72мм

l = 2.5м

l = 6м

a

100×100×10

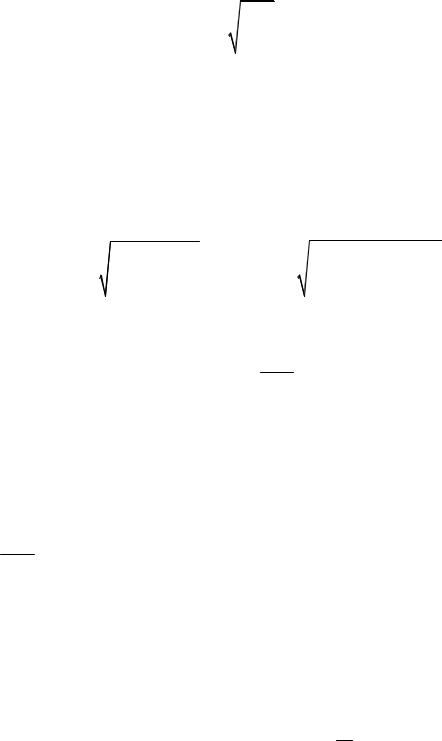
Рис. 5.6 Рис. 5.7

A = bh ; J

z

=

bh3

;i

z

=

J

z

=

h

=

7,2

= 2,08см,i

y

=

b

=

3,8

=1,10см.

бр

12

Aбр

12

12

12

12

Далі обчислюємо гнучкості стержня відносно головних осей інерції

λz

=

ν

l

=

1 2,5

=120,19

і λy =

νyl

=

0,5 2,5

=113,64 .

z

iz

2,08 10−2

iy

1,1 10−2

Оскільки λz>λy>100, то втрата стійкості стержня відбудеться внаслідок випучення відносно осі z, а для визначення допустимої стискаючої сили треба використати формулу Ейлера (5.4)

F ≤	π 2 EJz		=	3,142 2,1 1011 0,038 0,0723	=97890Н.
				(1 2,5)2 4
	(ν	l)2 n
	z	ст

[F]=97,9кH.

Приклад 5.6. Визначити розмір сторони a поперечного перерізу стійки (рис. 5.7) і довжину вільної гілки (відстань між з’єднуючими планками). Матеріал стійки – сталь Ст.3; [σ–]=160 МПа.

Випишемо із сортаменту необхідні геометричні характеристики кутників 100×100×10 (рис. 5.7).

A1=19,2 см2; Jz1 =179 см4; imin=1,96 см; z0=2,83 см.

Далі з умови стійкості (5.7) визначаємо необхідне значення коефіцієнта ϕ :

141

	ϕ ≥	F			=	1000 103	= 0,814.
		A [σ	−	]		4 19,2 10−4 160 106
		бр

За табл. 5.2 знаходимо відповідну цьому значенню φ гнучкість стійки λ=69,2. Врахуємо, що

λ =	νl	=	νl				J			νl 2
	imin							min	=	.
				Jmin			Aбр
										λ

Aбр

Виразимо Jmin через геометричні характеристики перерізу:

a

2

= 4A1 .

Jmin = 4 Jz1

+ A1

− z0

; Aбр

2

Jz

a

2

νl 2

Тепер маємо

1

+

− z0

=

. Звідси знаходимо

A1

2

λ

νl 2

Jz

1

1600 2

179

a = 2

z0 +

−

1

=

2

2,83

+

−

= 21,89см.

λ

A1

69,2

19,2

Довжину вільної гілки визначимо з умови

λв =νiввminlв = λ .

Якщо прийняти νв =1 і врахувати, що iв min =i1 min, то lв = λ i1min = 69,2 1,96 =135,6 см.

При цьому треба поставити n =	l	+1=5,42 пл. Приймаємо n=6, тоді
	lв

lв = n l−1 =120 см, тобто з’єднуючі планки треба поставити через 120 см.

5.3. Приклади для самостійного розв’язання

Приклад 5.7. Визначити діаметр d контрштока компресора (рис. 5.8), якщо nст = 3. Матеріал – сталь Ст.5; Е =2·105 МПа.

Приклад 5.8. Для стержня (рис. 5.9) потрібно визначити розміри поперечного перерізу в двох варіантах:

а) кільцевий переріз із відношенням α = Dd =0,75;

142

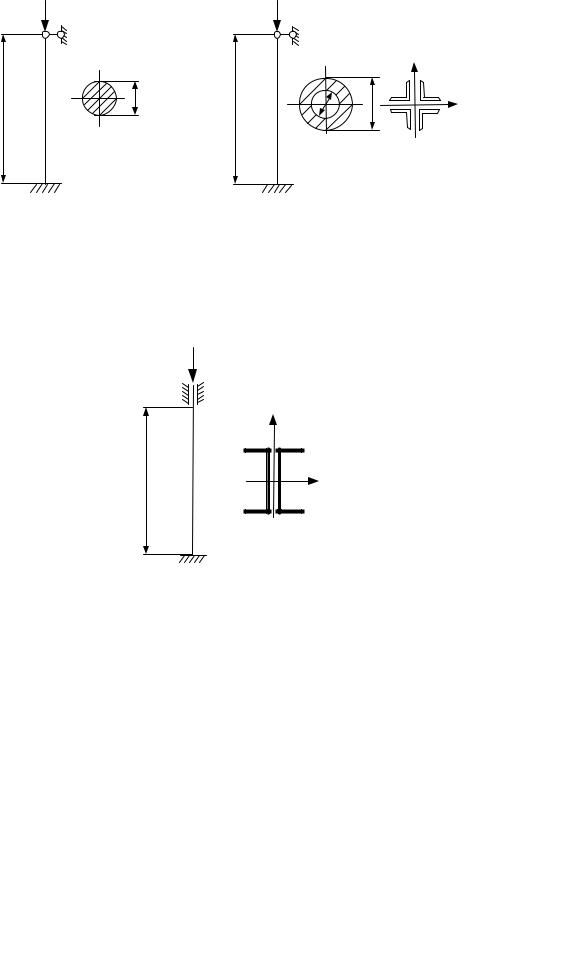
б) із чотирьох рівнобічних кутників, зварених по всій довжині. Матеріал – сталь Ст.3, [σ–]=160 МПа.

l = 0.5м

l = 3.4м

Рис. 5.8

Рис. 5.9

Приклад 5.9. Визначити допустиме навантаження для стійки (рис. 5.10), що складається з двох жорстко сполучених між собою швелерів № 10. Матеріал – сталь Ст.3; [σ–]=160 МПа.

l = 4м

Рис. 5.10

Приклад 5.10. Перевірити стійкість чавунної колони висотою ℓ=6 м, стиснутою силою F=450 кH. Переріз колони – кільце із зовнішнім діаметром D = 250 мм і товщиною стінки δ = 20 мм. Кінці колони шарнірно закріплені. Основне допустиме напруження на стискання чавуну [σ–]= 100 MПа.

143

РОЗДІЛ 6. РОЗРАХУНКИ НА МІЦНІСТЬ ПРИ НАПРУЖЕННЯХ, ЩО ЦИКЛІЧНО ЗМІНЮЮТЬСЯ У ЧАСІ

6.1. Основні відомості з теорії

Зміна напружень у деталях машин і елементах конструкцій у часі може бути хаотичною або закономірною – циклічною. Для деталей машин характерною є циклічна зміна напружень у часі, що звичайно задається функцією

σ =σc +σα sinωt .

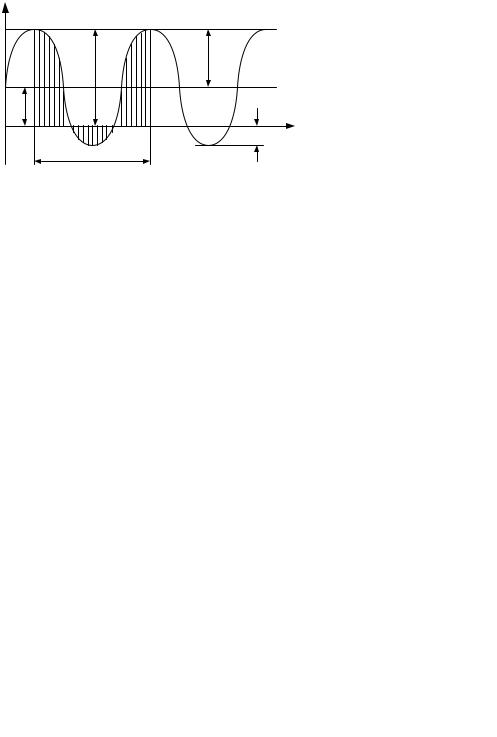
Графік функції (6.1) наведений на рис. 6.1.

σ

	a
max	σ
σ

σ c

σ min

Рис. 6.1

(6.1)

t

Проміжок часу Т, через який напруження в даній точці приймають ті саме значення, називається періодом.

Сукупність усіх напружень за один період називається циклом зміни напружень.

σmax і σmin – максимальне і мінімальне напруження циклу;

σс і σα – середнє напруження та амплітуда циклу.

Зрис. 6.1 видно, що

		σmax = σс +σα ; σmin = σс −σα ;								(6.2)
σ	с	=	σmax +σmin	;	σ	=		σmax −σmin	.	(6.3)
		2			α	2
Відношення					σmin
			r =							(6.4)
					σmax

144

називається коефіцієнтом асиметрії циклу. Він змінюється в межах від −∞ до +∞.

При r = −1 цикл називається симетричним. При r ≠ −1 цикл називається асиметричним.

Цикли, що мають однакові коефіцієнти асиметрії, називаються подібними.

Процес руйнування матеріалу при дії повторно-змінних напружень називається втомленістю, а здатність його чинити опір таким напру-женням – витривалістю.

Практика показує, що при дії повторно-змінних напружень деталі машин руйнуються при σmax < σв або навіть при σmax < σT . Проте для чорних металів (сталі, чавуну і т.п.) існує таке найбільше максимальне напруження циклу, при якому матеріал витримує, не руйнуючись, необмежену кількість циклів. Це напруження називається межею витривалості σr . Його визначають

дослідним шляхом, у результаті випробувань матеріалу на витривалість (утому). Досліди показують, що зразок із чорних металів, що витримав 107 циклів, не руйнується вже при як завгодно великій кількості циклів. Ця кількість циклів 107 називається базовою. Для кольорових металів і сплавів (міді, алюмінію, бронзи та ін.) не існує дійсної базової кількості циклів, а отже, і межі витривалості. Для них приймають за умовну базову кількість циклів 108, а під межею витривалості розуміють найбільше максимальне напруження циклу, при якому зразок витримує базову кількість циклів 108.

Для орієнтовного визначення межі витривалості чорних металів при симетричному циклі і розтяганні-стисканні σ0−1 , згинанні σзг−1 і крученні τ−1 можна скористатися відомими [1] емпіричними залежностями:

σ0−1 = 0,28σв , σ−зг1 = 0,4σв , τ−1 = 0,22σв .

(6.5)

Для кольорових металів і сплавів ці залежності менш стійкі, наприклад, для σзг−1 формула має вигляд

σ−зг1 = (0,24 + 0,5)σв .

(6.6)

Межа витривалості залежить не тільки від властивостей матеріалу, з якого виготовлена деталь, але і від коефіцієнта асиметрії циклу r, концентрації напружень, чистоти обробки поверхні, абсолютних розмірів деталі та інших менш значних факторів (середовище випробувань, тренувань зразка, пауз у випробуваннях та ін.).

Вплив коефіцієнта асиметрії циклу r на межу витривалості матеріалу визначають у практичних розрахунках за схематизованою діаграмою втомлюваної міцності (рис. 6.2).

145

Пряма СЕ відтинає на координатних осях відрізки, які дорівнюють межі текучості матеріалу σт. Тому рівняння її можна записати у вигляді

σс	+	σα = 1.	(6.7)
σт		σт

З(6.7) випливає, що на СЕ σс + σα = σт або, відповідно до формули (6.2),

σmax = σт . Вище прямої СЕ σmax > σт , тому вона відтинає від діаграми зону

великих пластичних деформацій ВDЕ. Чотирикутник, що залишився, ОАDЕ – зона безпечних циклів по втомленості і текучості.

Для визначення межі витривалості матеріалу σr при циклі з

коефіцієнтом асиметрії r необхідно провести з початку координат промінь під кутом

	θ = arctg	1	− r	(6.8)
		1	+ r

до осі абсцис до перетинання з прямою АD у точці N (σ′с;σ′α ). Положення цього променя також визначається точкою K (σс;σα ). Тому що за форму-

лою (6.2)

	σmax = σс +σα , то σr = σ′с +σα′ .						(6.9)
	σa
T	−1
σ
σ				ϕ0
	θ	а			γ	σc
		σ
	σc		σT
				σв
			Рис. 6.2

Для аналітичного визначення межі витривалості матеріалу більш зручно користуватися формулою

	σr =		2 σв σ−1	.	(6.10)
		(1	− r)σв + (1+ r)σ−1

З діаграми (рис. 6.2) видно, що σr має найменше значення приσс = 0 .

Отже, межа витривалості матеріалу при симетричному циклі ( r = −1) має найменше значення.

Для дотичних напружень τ випрямлена діаграма граничних напружень має такий же вигляд, як і для нормальних напружень [1].

146