4. Нормальне наближення

Нехай випадкова величина має біноміальний розподіл.

Якщо значення параметра 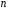великі, то безпосереднє обчислення ймовірності подій, пов'язаних з цією випадковою величиною, технічно складно. В цих випадках можна використовувати наближення біноміального розподілу розподілом Пуассона і нормальним розподілом (наближенняМуавра-Лапласа).

Наближення нормальним розподілом використовується в ситуаціях, коли , афіксовано. Це наближення можна розглядати як окремий випадок центральної граничної теореми, застосування якої засноване на представленні випадкової величиниу вигляді суми доданків. Наближення засноване на тому, що за вказаних умов розподіл нормованої величини

, де ,

близький до стандартного нормального.

Локальна теорема Муавра-Лапласа

Дана теорема використовується для наближеного обчислення ймовірностей окремих значень биноміального розподілу. Вона стверджує, що рівномірно по всім значенням має місце

,

де — щільність стандартного нормального розподілу,. (функція Гаусса.)

Інтегральна теорема Муавра-Лапласа

На практиці необхідність оцінки ймовірності окремих значень, яку дає локальна теорема Муавра-Лапласа, виникає нечасто. Набагато більш важливо оцінювати ймовірність подій, що включають в себе множину значень. Для цього використовується інтегральна теорема, яку можна сформулювати в наступному виді: При 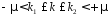, і

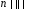
де — функція розподілу стандартного нормального закону (функція Лапласа).

Відзначимо, що функція не залежить ні від яких параметрів. Отже, границя в теоремі Муавра-Лапласа є універсальною, оскільки вона не залежить від параметра, який є в дограничному виразі. Насправді, ця теорема є окремим випадком іншої, ще більше універсальної центральної граничної теореми.

На практиці рішення про те, наскільки слід довіряти нормальному наближенню, приймають виходячи з величини 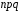. Чим вона більша, тим менше буде погрішність наближення.

Помітимо, що асимптотичний результат не зміниться, якщо замінити нестрогі нерівності на строгі і навпаки. Гранична ймовірність від такої заміни також не зміниться, оскільки нормальний розподіл абсолютно неперервний і ймовірність набути будь-якого конкретного значення для нього дорівнює нулю. Проте початкова ймовірність від такої заміни може змінитися, що вносить у формулу деяку неоднозначність. Для великих значень зміна буде невелика, проте для невеликихце може внести додаткову погрішність.

Для усунення цієї неоднозначності, а також підвищення точності наближення рекомендується задавати події, які нас цікавлять, у вигляді інтервалів з напівцілими межами. При цьому наближення виходить точніше. Це пов'язано з тим інтуїтивно зрозумілим міркуванням, що апроксимація кусково-сталої функції (функції розподілу біноміального закону) за допомогою неперервної функції дає точніші наближення між точками розриву, чим в цих точках.

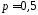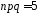Приклад. Нехай ,. Оцінимо ймовірність того, що число успіхів буде відрізнятися від найбільш ймовірного значення 10 не більше ніж на 3. Відзначимо, що значеннядуже мале, тому застосування нормального наближення тут досить ненадійно.

Точна ймовірність даної події дорівнює

.

Застосуємо нормальне наближення з такою розстановкою нерівностей: (знизу строга, зверху нестрога):

.

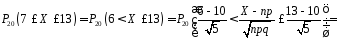
Помилка наближення дорівнює 0,8846–0,8733=0,0113.

Тепер побудуємо наближення, використовуючи інтервал з кінцями в напівцілих точках:

.

Помилка наближення дорівнює 0,8846–0,8724=0,0022 – приблизно в 5 разів менше, ніж в попередньому випадку.