
- •Лекція № 10 Тема: Біноміальний, рівномірний і нормальний розподіл ймовірностей
- •1. Біноміальний розподіл ймовірностей
- •1.1. Розподіл Бернуллі
- •2. Рівномірний розподіл
- •2.1 Рівномірний дискретний розподіл
- •2.2 Рівномірний неперервний розподіл
- •3. Нормальний розподіл ймовірностей
- •4. Нормальне наближення
- •5. Розподіли, пов’язані з нормальним
- •1) Розподіл 2 (хі-квадрат)
- •2) Розподіл Стьюдента (-розподіл)
- •6. Оцінки параметрів розподілу випадкових величин
- •7. Оцінки параметрів біноміального розподілу
- •8. Оцінки параметрів нормального розподілу
- •8.1 Довірчий інтервал для математичного сподівання при відомій дисперсії
- •8.2 Довірчий інтервал для математичного сподівання при невідомій дисперсії
- •8.3. Довірчий інтервал для дисперсії при відомому математичному сподіванні
- •8.4. Довірчий інтервал для дисперсії при невідомому математичному сподіванні
- •8.5. Довірчий інтервал для середнього квадратичного відхилення
7. Оцінки параметрів біноміального розподілу
У
цього розподілу два параметри:
 (число випробувань) і
(число випробувань) і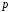 (ймовірність успіху в одному випробуванні).
Часто зустрічається ситуація, коли
(ймовірність успіху в одному випробуванні).
Часто зустрічається ситуація, коли відоме, а
відоме, а невідоме, тобто відоме число випробувань,
але не відома ймовірність успіху в
одному випробуванні.
невідоме, тобто відоме число випробувань,
але не відома ймовірність успіху в
одному випробуванні.
Для цього розподілу

Точковою
оцінкою
 параметра
параметра є
є
 .
.
Особливо
важливий окремий випадок, коли
 ,
в цьому випадку отримуємо
,
в цьому випадку отримуємо .
Коли
.
Коли ,
, або
або (успіх або невдача), тому
(успіх або невдача), тому дорівнюватиме числу успіхів. Якщо
позначити цю суму або число успіхів
через
дорівнюватиме числу успіхів. Якщо
позначити цю суму або число успіхів
через ,
отримаємо:
,
отримаємо:
 .
.
Оцінка
 є незміщеною оцінкою параметра
є незміщеною оцінкою параметра .
.
Приклад. Спортсмен вистрілив у ціль 20 разів, а влучив 15 разів. Визначити ймовірність влучення при одному пострілі.
Розв’язання:
 .
.
Знайдемо
довірчий інтервал, який покриває
невідомий параметр
 з надійністю
з надійністю .
Відомо, що біноміальний розподіл може
бути наближений за допомогою нормального
розподілу. Якщо оцінювана ймовірність
не дуже мала і не дуже велика (
.
Відомо, що біноміальний розподіл може
бути наближений за допомогою нормального
розподілу. Якщо оцінювана ймовірність
не дуже мала і не дуже велика ( ),
то можна вважати, що розподіл випадкової
величини
),
то можна вважати, що розподіл випадкової
величини близький до нормального. Цим допущенням
можна користуватися, якщо
близький до нормального. Цим допущенням
можна користуватися, якщо і
і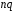 більше 4. Виберемо при заданій надійності
більше 4. Виберемо при заданій надійності числа
числа ,
, (нижню і верхню межу довірчого інтервала)
так, щоб виконувалися нерівності
(нижню і верхню межу довірчого інтервала)
так, щоб виконувалися нерівності і
і .
Тоді ймовірність попадання значення
.
Тоді ймовірність попадання значення в інтервал (
в інтервал ( ,
, )
буде дорівнювати
)
буде дорівнювати
 .
Для практичного знаходження довірчих
інтервалів з надійністю
.
Для практичного знаходження довірчих
інтервалів з надійністю і
і при
при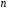 від 1 до 30, а також при
від 1 до 30, а також при і
і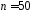 можна скористатися наперед складеними
таблицями, які можна знайти в довідниках
з математичної статистики.
можна скористатися наперед складеними
таблицями, які можна знайти в довідниках
з математичної статистики.
При великих об'ємах вибірки можна обійтися наближеною побудовою довірчого інтервалу. Скористаємося формулою ймовірності відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях
 .
.
Позначимо
 і, за допомогою таблиці значень функції
Лапласа, розв’яжемо рівняння
і, за допомогою таблиці значень функції
Лапласа, розв’яжемо рівняння .
З набутого значення
.
З набутого значення знайдемо
знайдемо .
Тоді
.
Тоді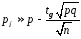 ,
, .
Щоб отримати довірчий інтервал, треба
виконати ще ряд перетворень, в результаті
чого при великому об'ємі вибірки наближене
значення для довірчого інтервалу має
вид.
.
Щоб отримати довірчий інтервал, треба
виконати ще ряд перетворень, в результаті
чого при великому об'ємі вибірки наближене
значення для довірчого інтервалу має
вид.
 .
.
Приклад.
При 20 пострілах спортсмен влучив у ціль
15 разів. Із надійністю
 побудувати довірчий інтервал довірчий
інтервал для ймовірності влучення при
одному пострілі.
побудувати довірчий інтервал довірчий
інтервал для ймовірності влучення при
одному пострілі.
Розв’язання.
Для побудови довірчого інтервалу
необхідно знати:
 ,
, ,
, .
З умови задачі маємо:
.
З умови задачі маємо: .
Точкова оцінка ймовірності влучення
знайдена в попередньому прикладі і
дорівнює
.
Точкова оцінка ймовірності влучення
знайдена в попередньому прикладі і
дорівнює
 .
.
Величина
 обчислюється з рівняння
обчислюється з рівняння
 .
.
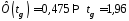 за
таблицею значень функції Лапласа.
за
таблицею значень функції Лапласа.
Знайдемо числові значення кінців довірчого інтервалу:
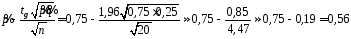 ;
;
 .
.
Таким чином, маємо:
 .
.
Отже,
з надійністю 0,95 (95% гарантії) інтервал
 покриває оцінюваний параметр
покриває оцінюваний параметр .
.
8. Оцінки параметрів нормального розподілу
У
цього розподілу два параметри: математичне
сподівання
 і дисперсія
і дисперсія .
Оцінками
.
Оцінками і
і параметрів
параметрів і
і є
є
 ,
,  .
.
Величина
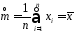 є незміщеною, спроможною і ефективною
оцінкою математичногосподівання,
тому її значення приймаємо за точкову
оцінку значення математичного сподівання.
є незміщеною, спроможною і ефективною
оцінкою математичногосподівання,
тому її значення приймаємо за точкову
оцінку значення математичного сподівання.
8.1 Довірчий інтервал для математичного сподівання при відомій дисперсії
Будемо
вважати, що дисперсія
 відома, тоді вибіркове середнє
відома, тоді вибіркове середнє – нормально розподілена випадкова
величина з параметрами
– нормально розподілена випадкова
величина з параметрами .
Для
такої випадкової величини ймовірність
попадання на симетричний відносно
математичного сподівання
інтервал
виражається через функцію Лапласа
.
Для
такої випадкової величини ймовірність
попадання на симетричний відносно
математичного сподівання
інтервал
виражається через функцію Лапласа
 ,
,
де
 .
При заданій надійності
.
При заданій надійності рівняння
рівняння можна розв’язати наближено за допомогою
таблиці значень функції Лапласа.
можна розв’язати наближено за допомогою
таблиці значень функції Лапласа.
Якщо
точного значення
 в таблиці значень немає, то потрібно
знайти два найближчих до нього значення,
одне більше, а інше менше, ніж
в таблиці значень немає, то потрібно
знайти два найближчих до нього значення,
одне більше, а інше менше, ніж ,
і знайти їх середнє арифметичне. Відоме
значення параметра
,
і знайти їх середнє арифметичне. Відоме
значення параметра дозволяє записати абсолютну похибку
дозволяє записати абсолютну похибку .
Тепер можна вказати симетричний інтервал
.
Тепер можна вказати симетричний інтервал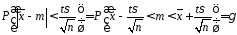 .
Отримане співвідношення означає, що
довірчий інтервал
.
Отримане співвідношення означає, що
довірчий інтервал покриває невідомий параметр
покриває невідомий параметр (математичне сподівання ) зймовірністю
(надійністю)
(математичне сподівання ) зймовірністю
(надійністю)
 , а точність оцінки
, а точність оцінки .
.
При
фіксованому об'ємі вибірки з оцінки
 виходить, що чим більше довірчаймовірність,
тим ширше межі довірчого інтервалу (тим
більше помилка в оцінці математичного
сподівання). Щоб знизити помилку в оцінці
значення, можна збільшити об'єм вибірки.
При цьому, щоб знизити відносну похибку
на порядок, необхідно збільшити об'єм
вибірки на два порядки.
виходить, що чим більше довірчаймовірність,
тим ширше межі довірчого інтервалу (тим
більше помилка в оцінці математичного
сподівання). Щоб знизити помилку в оцінці
значення, можна збільшити об'єм вибірки.
При цьому, щоб знизити відносну похибку
на порядок, необхідно збільшити об'єм
вибірки на два порядки.
Приклад
1.
За даними спостережень випадкової
величини
 знайти довірчий інтервал для математичного
сподівання
знайти довірчий інтервал для математичного
сподівання з надійністю
з надійністю ,
якщо відома дисперсія
,
якщо відома дисперсія .
Вибірка представлена таблицею.
.
Вибірка представлена таблицею.
|
Інтервали
|
(10;20) |
(20;30) |
(30;40) |
(40;50) |
|
|
Середини інтервалів |
15 |
25 |
35 |
45 |
|
|
частоти |
10 |
45 |
30 |
15 |
100 |
Розв’язання.
Знайдемо
об'єм вибірки, для чого підсумуємо
вказані в таблиці частоти:
 .
Середнє вибіркове значення обчислимо
за формулою
.
Середнє вибіркове значення обчислимо
за формулою
 .
.
За
заданою надійністю
 знайдемо, за допомогою таблиці, параметр
знайдемо, за допомогою таблиці, параметр :
: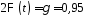 ,
звідки
,
звідки ,
, .
Отримаємо довірчий інтервал для
математичного сподівання
.
Отримаємо довірчий інтервал для
математичного сподівання
 .
.
Проведемо обчислення і остаточно запишемо
 .
.
Таким
чином, інтервал
 покриває параметр
покриває параметр з надійністю
з надійністю при відомій дисперсії
при відомій дисперсії .
.


