При плоском поперечном изгибе

. (7.18)

Складывая полученные значения для элементарной работы внутренних сил и интегрируя по длине стержня, можно получить полную работу внутренних сил для общего случая действия сил на стержень при возникновении всех шести силовых факторов:

(7.19)

Потенциальная энергия при возникновении всех шести внутренних силовых факторов с учетом принимает вид:

(7.20)

Из приведенной формулы видно, что потенциальная энергия деформации является квадратичной функцией обобщенных сил или обобщенных перемещений, так как последние линейно связаны с обобщенными силами. Следовательно, потенциальная энергия деформации всегда положительна. Ее величина не зависит от порядка нагружения и целиком определяется окончательными значениями усилий и перемещений. Отметим также, что потенциальная энергия как квадратичная функция обобщенных нагрузок не подчиняется принципу независимости действия сил. Это значит, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, вызванных действием каждой нагрузки в отдельности. Закон независимости действия сил при вычислении потенциальной энергии применим лишь в тех случаях, когда перемещение по направлению одной обобщенной силы, вызванное действием другой силы, равно нулю.

Приведенные выражения для потенциальной энергии деформации получены для статического приложения нагрузок при сохранении равновесия в течение всего процесса нагружения. Следует сказать, что полученные формулы сохраняют силу и при любом способе приложения нагрузок, лишь бы значения сил и деформаций были связаны линейной зависимостью и относились к тому моменту, когда установится равновесие конструкции.

Рассмотрим несколько примеров определения перемещений с применением потенциальной энергии деформации.

Пример 7.1.Определить величину потенциальной энергии деформации в шарнирно-стержневой системе (Рис.7.5), нагруженной в узле В вертикальной силойкН. Стержни АВ и ВС имеют одинаковые площади поперечного сечениясм²и изготовлены из одного материалаМПа. Найти (в мм) вертикальное перемещение узла В.

Рис.7.5

Решение:

1. Находим усилия в стержнях АВ и ВС:

; (а)

. (б)

Из уравнения (б) находим: кН; из уравнения (а) находим :кН.

2. Определяем потенциальную энергию системы:

Нм.

3. Находим вертикальное перемещение узла В. Представим потенциальную энергию деформации как половину произведения силы , приложенной в узле, на вертикальное перемещение узла В:

.

Откуда: ммм.

Пример 7.2. Вычислить потенциальную энергию деформации балки на двух опорах (Рис.7.6), нагруженную силой кН. Определить перемещение под силой и посредине пролета. Жесткость поперечного сечения балки принять равнойкНм².

Рис.7.6

Решение:

1. Вычисляем опорные реакции: ;.

2. Вычисляем изгибающий момент на каждом участке:

; .

3. Определяем потенциальную энергию деформации:

Нм.

4. Находим прогиб под силой. Для этого вычислим работу, которую совершает сила на перемещении балки:

; ,

откуда

ммм.

5. Находим прогиб посредине балки при . Получим:

ммм.

7.4. Определение перемещений методом Мора

Метод Мора является самым общим методом определения перемещений в стержневых системах. В известном смысле этот метод является универсальным, так как способен находить перемещения для различных видов деформации и в случаях сложной деформации.

Рассмотрим статически определимую раму, нагруженную в сечении К сосредоточенной силой (Рис.7.7,а). Рамой называется стержневая система, элементы которой соединены в узлах жестко, без взаимного поворота сечений в узлах.

Рис.7.7

Требуется определить вертикальное перемещение сечения , вызванное внешней силой, приложенной в сечении.

Поступим следующим образом: сначала приложим в сечении фиктивную сосредоточенную силу. Рама деформируется и сечениепереместится на величину. Двойная индексация у перемещений означает следующее: первый индекс означает наименование сечения, в котором прикладывается фиктивная сила, т.е. наименование того сечения, в котором определяется перемещение. Второй индекс означает причину, вызвавшую это перемещение. В данном случае – это сила. В более общем случае это может быть любая нагрузка, приложенная к конструкции и вызывающая деформацию.

Затем приложим к раме действительную силу , после чего рама деформируется еще больше. При этом сечениепереместится на величину, а сечение на величину . Перемещениеи есть то перемещение, которое и следует определить.

Для его определения поступим следующим образом. Вычислим работу, которую совершают внешние силы при статическом нагружении:

. (7.21)

В последнем члене уравнения (7.21) отсутствует коэффициент , так как в момент приложения к раме силыфиктивная силаявляется неизменной по величине и направлению.

Вычислим потенциальную энергию деформации с учетом, что в раме возникают продольная сила и изгибающий момент, и их действие происходит одновременно (влиянием поперечной силы будем пренебрегать):

(7.22)

На основании (7.3) работа внешних сил (7.21) должна быть равна накопленной потенциальной энергии(7.22). Приравняем их.

При составлении выражения для работы внешних сил мы использовали принцип независимости действия сил (принцип суперпозиции). Но при вычислении потенциальной энергии принцип суперпозиции в данном случае не применим, так как потенциальная энергия является квадратичной функцией и накапливается она в результате одновременного действия сил и. В связи с этим потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, вызванных действием каждой силы в отдельности. Очевидно, в уравнении (7.22) имеются члены, которые не появились бы при суммировании потенциальных энергий от действия каждой силы в отдельности. Выясним, что это за члены и какой части в уравнении работ (7.21) они соответствуют.

Для этого вычислим величину потенциальной энергии деформации, накапливаемой в раме при действии каждой силы в отдельности:

При действии только силы :

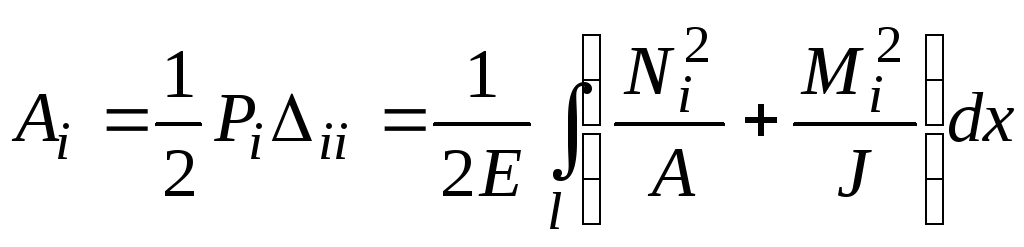. (7.23)

При действии только силы :

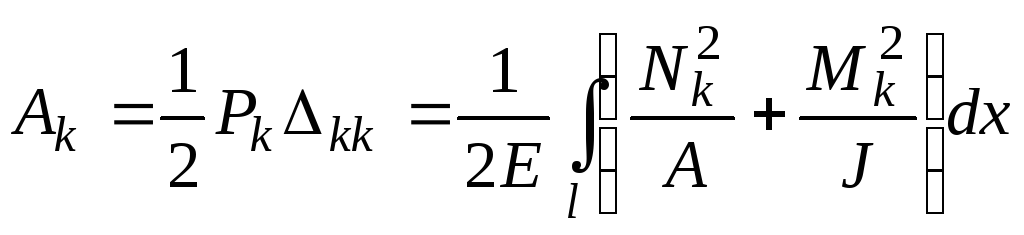. (7.24)

Перепишем выражение (7.21) в виде:

(7.25)

и подставим в это уравнение выражения (7.23) и (7.24). Получим:

.

После взаимных сокращений получаем:

. (7.26)

Положим . Тогда из выражения (7.26) находим искомое перемещение:

. (7.27)

Выражение (7.27) и представляет собой интеграл Мора. Здесь: и продольная сила и изгибающий момент, возникающие в системе от действия внешней силы .

Как уже отмечалось, метод Мора является методом универсальным. Для самого общего случая нагружения, когда возникают все шесть внутренних силовых факторов, интеграл Мора принимает вид:

(7.28)

В большинстве случаев при определении перемещений в балках и рамах можно пренебречь влиянием продольной деформации и деформации сдвига, учитывая лишь перемещения, вызываемые изгибом и кручением. Тогда формула (7.28) для плоской системы принимает вид:

. (7.29)

При пространственном нагружении интеграл Мора записывается следующим образом:

(7.30)

При расчете шарнирных ферм, образованных прямыми стержнями, в формуле Мора сохраняется лишь член, содержащий продольную силу:

(7.31)

Эта формула носит название формулы Максвелла.

Сформулируем следующий порядок определения перемещений по методу Мора:

1. Строим вспомогательную систему, которую нагружаем единичной силой в сечении, где требуется определить перемещение. Определяя линейные перемещения, в заданном направлении прикладываем единичную силу; определяя угловые перемещения, прикладываем единичный момент.

2. Для каждого участка системы выписываем выражения силовых факторов в произвольном сечении заданной (,,) и вспомогательной (,,) систем.

3. Вычисляем интегралы Мора (по участкам в пределах всей системы). При расчете плоских рам и балок применяем формулу (7.29), при расчете плоских ферм – формулу (7.31).

4. Если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичной силы. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичной силы.

Рассмотрим примеры применения метода Мора для определения перемещений в стержневых системах.

Пример 7.3. Используя формулу Максвелла, найти вертикальное перемещение узла В (в мм) фермы, изображенной на рис.7.8,а, если жесткости стержней фермы одинаковы кН.

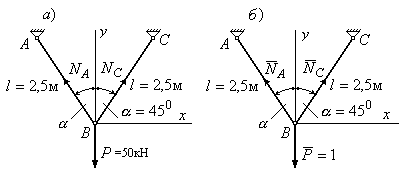
Рис.7.8

Решение:

1. Определяем грузовые усилия в стержнях фермы:

; (а)

. (б)

Из уравнения (а) устанавливаем, что . Из уравнения (б) находим:

.

2. Изображаем единичное состояние системы (Рис.7.8,б) и аналогичным образом находим усилия в стержнях фермы при единичном состоянии:

.

3. Подставляем полученные выражения для усилий в грузовом и единичном состояниях в формулу Максвелла (7.31) и перемножаем. Получаем:

ммм.

Пример 7.4. Определить с помощью метода Мора прогиб и угол поворота в сечении В для балки, изображенной на рис. 7.9,а, если жесткость поперечного сечения балки равна кНм².

Рис.7.9

Решение:

1. Изображаем грузовое состояние балки (Рис.7.9,а), нагружая балку в сечении В сосредоточенной силой, равной единице, и записываем выражение для изгибающего момента в сечении :

. (в)

2. Изображаем первое единичное состояние балки (Рис.7.9,б) и записываем выражение для единичного изгибающего момента в сечении :

. (г)

3. Подставляем выражения (в) и (г) в формулу Мора (7.29) и интегрируем:

ммм.

4. Изображаем второе единичное состояние (Рис.7.9,в), нагружая балку в сечении В сосредоточенной парой сил, равной единице, и записываем выражение для изгибающего момента в сечении :

. (д)

5. Подставляем выражения (в) и (д) в формулу Мора (7.29) и интегрируем:

рад.