7.8. Теорема Кастильяно. Теорема Лагранжа

Пусть упругая система статически нагружена произвольной нагрузкой и некоторой обобщенной силой(Рис.7.17). Вычислим потенциальную энергию, накопленную при деформации системы. С этой целью для удобства примем следующий порядок нагружения. Вначале нагружаем систему силой. Перемещение точки приложения силы по ее направлению и от ее действия обозначим. Затем прикладываем нагрузку.

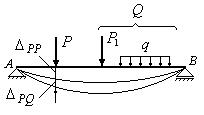
Рис.7.17

В результате дополнительной деформации сила получит перемещение. Полное (обобщенное) перемещение точки приложения силы

. (7.42)

Потенциальная энергия деформации, накопленная в системе, будет численно равна работе внешних сил:

, (7.43)

где энергия, накопленная в результате деформирования системы только силами, численно равная работе силна вызванных ими перемещениях.

Второй член в формуле (7.43) не содержит , так как на перемещении, сила, выполняя работу, не изменяла своего значения. Так как, то формулу (7.43) можно записать в виде:

. (7.44)

Продифференцируем выражение (7.44) по силе с учетом равенства (7.42):

.

Таким образом,

. (7.45)

Перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии по этой силе.

Эта теорема носит имя итальянского механика и инженера Карло Альберто Кастильяно и является одной из основных в строительной механике; выведенная первоначально для шарнирных ферм, она была обобщена автором на упругое тело любого вида. В связи с широким внедрением в расчетную практику метода Мора способ Кастильяно был вытеснен из практики определения перемещений в стержневых системах. Однако он остается общим методом определения перемещений в нестержневых системах (пластинках, оболочках и деталях, все три измерения которых имеют один порядок).

Заметим, что согласно формуле (7.44) вторая производная от потенциальной энергии по обобщенной силе равняется

. (7.46)

Учитывая, что является строго положительной величиной, вторая производная от потенциальной энергии по обобщенной силе также является положительной величиной.

Для плоской системы, пренебрегая влиянием продольной и поперечной сил, потенциальную энергию запишем в виде:

.

Применяя правило дифференцирования по параметру, находим:

. (7.47)

Чтобы определить линейное или угловое перемещение в сечении, где по условию задачи сила отсутствует, в этом сечении следует приложить соответствующую фиктивную обобщенную силу. Далее, написав выражение для потенциальной энергии от системы сил, включая указанную фиктивную силу, следует взять ее производную по этой фиктивной силе и в полученном выражении для перемещения приравнять фиктивную нагрузку нулю.

Выразив потенциальную энергию деформации в функции независимых перемещений , можно показать, чточастная производная от потенциальной энергии по любому перемещению равна силе, действующей по направлению перемещения, т.е.:

. (7.48)

Сформулированная теорема была установлена французским математиком и механиком Жозефом Луи Лагранжем и носит его имя.

Рассмотрим несколько примеров применения теорем Кастильяно и Лагранжа.

Пример 7.7. Используя теорему Кастильяно, определить прогиб и угол поворота в сечении В для балки, изображенной на рис.7.18, если жесткость поперечного сечения балки кНм².

Рис.7.18

Решение:

1. Добавим в сечении В сосредоточенную фиктивную силу и запишем выражение для изгибающего момента с учетом этой силы:

. (а)

2. Возьмем частную производную от изгибающего момента в выражении (а) по фиктивной силе:

. (б)

3. Подставим выражения (а) и (б) в формулу (7.47). Учитывая, что , получим:

ммм.

4. Для определения угла поворота в сечении В добавим в этом сечении фиктивный момент , запишем выражение для изгибающего момента в сечениис учетом этого момента:

. (в)

5. Возьмем частную производную по :

. (г)

и подставим выражения (в) и (г) в формулу (7.47). Учитывая, что , получим угол поворота в сечении В:

рад.

Пример 7.8.Определить величину силы, приложенной к статически неопределимой стержневой система в точке В, если опускание узла Вмм (Рис.7.19). Жесткость поперечного сечения одинакова для всех стержней и равнаН. Угол наклона крайних стержней. Длина крайних стержней №1 и №2м. Длина среднего стержня №3 с учетом наклона крайних стержнейм.

Рис.7.19

Решение:

1. Выразим деформации стержней фермы через перемещение точки В:

; .

2. Выразим усилия в стержнях фермы через перемещение точки В:

; .

3. Вычислим потенциальную энергию деформации, которая накапливается в системе:

.

5. Возьмем частную производную от выражения потенциальной энергии по :

Н.