12.3. Просторове (складне) згинання

Просторовим згинанням називається такий вид складного опору, при якому у поперечному перерізі бруса діють тільки згинальні моменти та. Повний згинальний момент при цьому не діє в жодній з головних площин інерції. Поздовжня сила відсутня. Просторове або складне згинання часто називаютьнеплоским згинанням, тому що зігнута вісь стержня не є плоскою кривою. Таке згинання викликається силами, що діють у різних площинах перпендикулярно до осі балки (Рис.12.4).

Рис.12.4

Дотримуючись порядку розв’язку задач при складному опорі, викладеному вище, розкладаємо просторову систему сил, наведену на рис. 12.4, на дві такі, щоб кожна з них діяла в одній з головних площин. В результаті одержуємо два плоских поперечних згинання – у вертикальній і горизонтальній площинах. З чотирьох внутрішніх силових факторів, що при цьому виникають у поперечному перерізі балки , будемо враховувати вплив тільки згинальних моментів. Будуємо епюри згинальних моментів, викликаних відповідно силами(Рис.12.4).

Аналізуючи епюри згинальних моментів, дістаємо висновку, що небезпечним є переріз А, тому що саме в цьому перерізі виникають найбільші за величиною згинальні моменти і . Тепер необхідно встановити небезпечні точки перерізу А. Для цього побудуємо нульову лінію. Рівняння нульової лінії з урахуванням правила знаків для членів, що входять у це рівняння, має вигляд:

. (12.7)

Тут прийнятий знак “” біля другого члена рівняння, тому що напруження в першій чверті, викликані моментом , будуть від’ємними.

Визначимо кут нахилу нульової лінії з додатнім напрямком осі(Рис.12.6):

. (12.8)

Рис.12.5

З рівняння (12.7) випливає, що нульова лінія при просторовому згинанні є прямою лінією і проходить через центр ваги перерізу.

З рис.12.5 видно, що найбільші напруження виникнуть у найбільш віддалених від нульової лінії точках перерізу №2 і №4. За величиною нормальні напруження в цих точках будуть однаковими, але за знаком відрізняються: у точці №4 напруження будуть додатними, тобто розтягальними, у точці №2 – від’ємними, тобто стискальними. Знаки цих напружень були встановлені за фізичною ознакою.

Тепер, коли небезпечні точки встановлені, обчислимо максимальні напруження в перерізі А и перевіримо міцність балки за допомогою виразу:

. (12.9)

Умова міцності (12.9) дозволяє не тільки виконати перевірку міцності балки, але і підібрати розміри її поперечного перерізу, якщо задано співвідношення його сторін.

12.4. Косе згинання

Косим називається такий вид згинання, при якому в поперечних перерізах балки виникають тільки згинальні моменти і, але на відміну від просторового згинання всі сили, що прикладені до балки, діють в одній (силовій) площині, яка не збігається з жодною з головних площин інерції. Цей вид згинання найбільш часто зустрічається в практиці, тому дослідимо його докладніше.

Розглянемо консольну балку, навантажену силою , як показано на рис. 12.6, і виготовлену з ізотропного матеріалу.

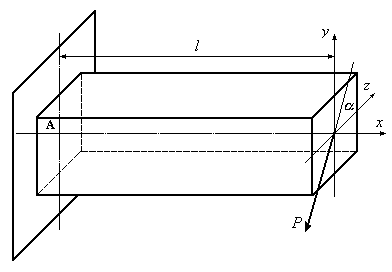
Рис.12.6

Так само, як і при просторовому згинанні, при косому згинанні відсутня поздовжня сила. Впливом поперечних сил при розрахунку балки на міцність будемо нехтувати.

Розрахункова схема балки, зображеної на рис.12.6, наведена на рис.12.7.

Розкладемо силу на вертикальнуі горизонтальнускладові і від кожної з цих складових побудуємо епюри згинальних моментів і .

Обчислимо складові повного згинального моменту в перерізі :

; .

Повний згинальний момент у перерізі дорівнює

.

Таким чином, складові повного згинального моменту можна виразити через повний момент таким чином:

; . (12.10)

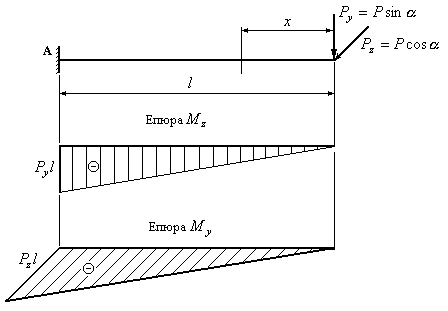
Рис.12.7

З виразу (12.10) видно, що при косому згинанні немає потреби розкладати систему зовнішніх сил на складові, тому що ці складові повного згинального моменту зв'язані одне з одним за допомогою кута нахилу сліду силової площини . У результаті відпадає потреба у побудові епюр складових моментів і . Досить побудувати епюру повного згинального моменту в силовій площині, а потім, скориставшись виразом (12.10), визначити складові повного згинального моменту в будь-якому перерізі балки. Отриманий висновок суттєво спрощує розв’язання задач при косому згинанні.

Підставимо значення складових повного згинального моменту (12.10) у формулу для нормальних напружень (12.2) при . Одержимо:

. (12.11)

Тут знак “” біля повного згинального моменту проставлений спеціально з тією метою, щоб автоматично одержувати правильний знак нормального напруження в розглянутій точці поперечного перерізу. Повний згинальний момент і координати точкиіберуться зі своїми знаками за умови, що в першому квадранті знаки координат точки приймаються додатними.

Формула (12.11) була отримана з розгляду окремого випадку косого згинання балки, затисненої одним кінцем і навантаженої на іншому зосередженою силою. Проте, ця формула є загальною формулою для обчислення напружень при косому згинанні.

Небезпечним перерізом, як і при просторовому згинанні в розглянутому випадку (Рис.12.6) буде переріз А, тому що в цьому перерізі виникає найбільший за величиною повний згинальний момент. Небезпечні точки перерізу А визначимо, побудувавши нульову лінію. Рівняння нульової лінії одержимо, обчислюючи за допомогою формули (12.11) нормальні напруження в точці з координатами і, що належить нульовій лінії, і дорівнюючи знайдені напруження нулю. Після нескладних перетворень одержимо:

(12.12)

або

, (12.13)

де  кут нахилу нульової лінії до осі (Рис.12.8).

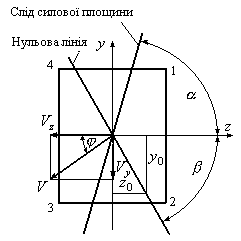
Рис.12.8

Досліджуючи рівняння (12.12) і (12.13), можна зробити деякі висновки про поведінку нульової лінії при косому згинанні:

 нульова лінія є прямою лінією;

 нульова лінія проходить через центр ваги поперечного перерізу;

 нульова лінія перетинає ті чверті координат, які не перетинає слід силової площини;

 нульова лінія в загальному випадку не перпендикулярна сліду силової площини. В окремому випадку при рівності моментів інерції і(круг, квадрат),, кутє доповненням кутадо 90⁰. З цього можна зробити висновок, що для перерізів, у яких моменти інерції відносно двох будь-яких взаємно перпендикулярних осей дорівнюють один одному (), косе згинання не виникає;

 якщо , то кутрозкривається більше, ніж прямій, нейтральна лінія відхиляється до тієї осі, відносно якої момент інерції є мінімальним.

З рис.12.8 випливає, що найбільші за величиною напруження виникають у точках перерізу, найбільш віддалених від нульової лінії. У розглянутому випадку такими точками є точки №1 і №3. Таким чином, при косому згинанні умова міцності має вигляд:

, (12.14)

де ;.

Якщо моменти опору перерізу відносно головних осей інерції можуть бути виражені через розміри перерізу, умову міцності зручно використовувати в такому вигляді:

. (12.15)

При підборі перерізів один з осьових моментів опору виносять за дужку і задаються співвідношенням . Знаючи,і кут, шляхом послідовних спроб визначають значенняі, що задовольняють умові міцності

. (12.16)

Для несиметричних перерізів, що не мають виступаючих кутів, використовується умова міцності у вигляді (12.14). У цьому випадку при кожній новій спробі підбору перерізу необхідно попередньо знову знайти положення нульової лінії і координати найбільш віддаленої від нульової лінії точки (). Для прямокутного перерізу. Задаючи співвідношення, з умови міцності (12.16) легко можна знайти величинуі розміри поперечного перерізу.

Розглянемо визначення переміщень при косому згинанні. Знайдемо прогин у перерізі консольної балки (Рис.12.9). Для цього зобразимо балку в одиничному стані і побудуємо епюру одиничних згинальних моментів в одній з головних площин. Будемо визначати повний прогин у перерізі, попередньо визначивши проекції вектора переміщеньна осіі. Проекцію вектора повного прогину на вісьзнайдемо, скориставшись формулою Мора:

. (12.17)

Проекцію вектора повного прогину на вісь знайдемо аналогічним способом:

. (12.18)

Повний прогин визначимо за формулою:

. (12.19)

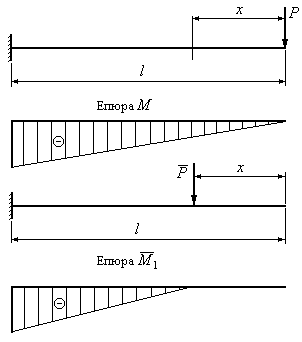
Рис.12.9

Слід звернути увагу на те, що при косому згинанні у формулах (12.17) і (12.18) при визначенні проекцій прогину на осі координат міняються лише члени, що знаходяться перед знаком інтеграла. Сам же інтеграл залишається сталим. При розв’язанні практичних задач будемо обчислювати цей інтеграл, користуючись методом Мора-Сімпсона. Для цього помножимо одиничну епюру на вантажну епюру(Рис.12.9), побудовану в силовій площині, а потім отриманий результат помножимо послідовно на коефіцієнти, відповідно,і. В результаті одержимо проекції повного прогинуіна осі координаті. Вирази для проекцій прогину для загального випадку навантаження, коли балка маєділянок, матимуть вигляд:

; (12.20)

(12.21)

Відкладемо знайдені значення для ,і(Рис.12.8). Вектор повного прогинускладає з віссюгострий кут, величину якого можна знайти за формулою:

, (12.22)

звідки

. (12.23)

Порівнюючи рівняння (12.22) з рівнянням нульової лінії (12.13), робимо висновок, що

або ,

звідки випливає, що нульова лінія і вектор повного прогину взаємно перпендикулярні: кутє доповненням кутадо 90⁰. Ця умова може бути використана для перевірки при вирішенні задач на косе згинання:

. (12.24)

Таким чином, напрям прогину при косому згинанні є перпендикулярним до нульової лінії. Звідси випливає важлива умова, що напрям прогину не збігається з напрямом діючої сили (Рис.12.8). Якщо навантаження являє собою плоску систему сил, то зігнута вісь балки лежить у площині, що не збігається з площиною дії сил. Балка перекошується стосовно силової площини. Ця обставина є підставою для того, що подібне згинання називають косим.

Приклад 12.1. Визначити положення нульової лінії (знайти кут ) для поперечного перерізу балки, зображеної на рис.12.10.

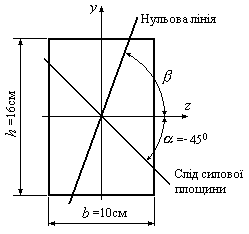
Рис.12.10

Розв’язок:

1. Кут до сліду силової площини будемо відкладати від додатного напряму осі. Кутзавжди будемо брати гострим, але з урахуванням знаку. Будь-який кут вважається додатним, якщо в правій системі координат його відкладають від додатного напряму осіпроти годинникової стрілки, і від’ємним, якщо кут відкладають за годинниковою стрілкою. У даному випадку кут вважається від’ємним ().

2. Визначаємо співвідношення осьових моментів інерції:

.

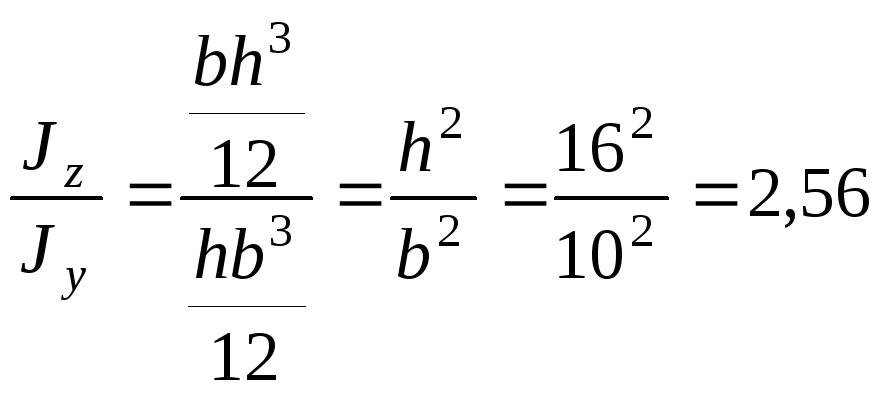3. Записуємо рівняння нульової лінії при косому згинанні у виді (12.13), звідки знаходимо кут :

; .

4. Кут виявився додатним, тому відкладаємо його від додатного напряму осіпроти годинникової стрілки до нульової лінії (Рис.12.10).

Приклад 12.2. Визначити величину нормального напруження в точці А поперечного перерізу балки при косому згинанні, якщо згинальний момент кНм, координати точкисм,см. Розміри поперечного перерізу балки і кут нахилу силової площининаведені на рис.12.11.

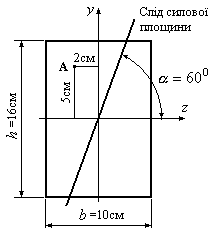
Рис.12.11

Розв’язок:

1. Обчислимо попередньо моменти інерції перерізу відносно осей і:

см⁴; см⁴.

2. Запишемо формулу (12.11) для визначення нормальних напружень у довільній точці поперечного перерізу при косому згинанні. При підстановці значення згинального моменту у формулу (12.11) слід врахувати, що згинальний момент за умовою задачі є додатним.

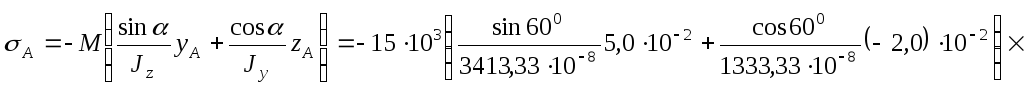
7,78 МПа.

Приклад 12.3. Визначити розміри поперечного перерізу балки, зображеної на рис.12.12,а. Матеріал балки – сталь з допустимим напруженням МПа. Співвідношення сторін задається. Навантаження і кут нахилу силової площининаведені на рис.12.12,в.

Розв’язок:

1. Для визначення положення небезпечного перерізу будуємо епюру згинальних моментів (Рис.12.12,б). Небезпечним є переріз А. Максимальний згинальний момент у небезпечному перерізі кНм.

2. Небезпечною точкою в перерізі А буде одна з кутових точок. Умову міцності запишемо у вигляді

,

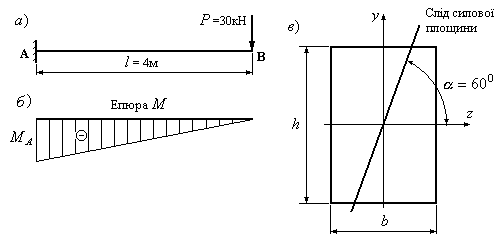
Рис.12.12

Звідки знайдемо осьовий момент опору , з огляду на те, що співвідношення:

см³.

3. Визначаємо розміри поперечного перерізу. Осьовий момент опору з урахуванням співвідношення сторіндорівнює:

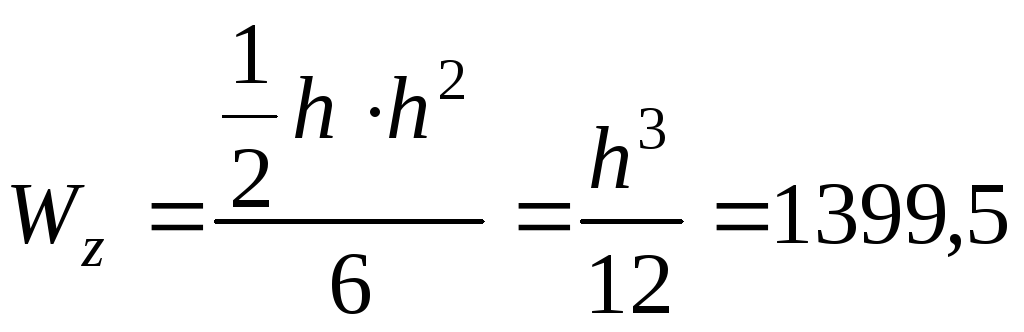см³, звідки

см; см.

Приклад 12.4. В результаті згинання балки центр ваги перерізу перемістився у напрямку, обумовленому кутом з віссю(Рис.12.13,а). Визначити кут нахилусилової площини. Форма і розміри поперечного перерізу балки наведені на рисунку.

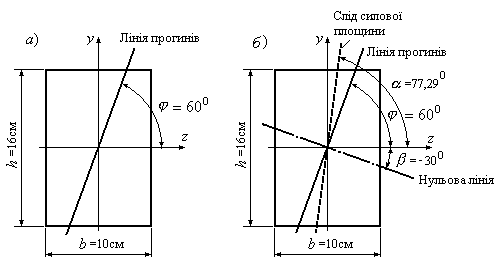
Рис.12.13

Розв’язок:

1. Для визначення кута нахилу сліду силової площини скористаємося виразом (12.22):

, звідки .

Співвідношення моментів інерції (див. приклад 12.1). Тоді

.

Відкладаємо це значення кута від додатного напряму осі(Рис.12.13,б). Слід силової площини на рис.12.13,б показаний штриховою лінією.

2. Виконаємо перевірку отриманого рішення. Для цього при знайденому значенні кута визначимо положення нульової лінії. Скористаємося виразом (12.13):

.

Звідки

.

Нульова лінія показана на рис.12.13 штрих-пунктірною лінією. Нульова лінія має бути перпендикулярною лінії прогинів. Перевіримо це:

.

Приклад 12.5. Визначити повний прогин балки в перерізі В при косому згинанні (Рис.12.14,а). Матеріал балки – сталь з модулем пружності МПа. Розміри поперечного перерізу і кут нахилу силової площининаведені на рис.12.14,б.

Розв’язок:

1. Визначимо проекції вектора повного прогину в перерізі Аі. Для цього побудуємо вантажну епюру згинальних моментів(Рис.12.14,в), одиничну епюру(Рис.12.14,г).

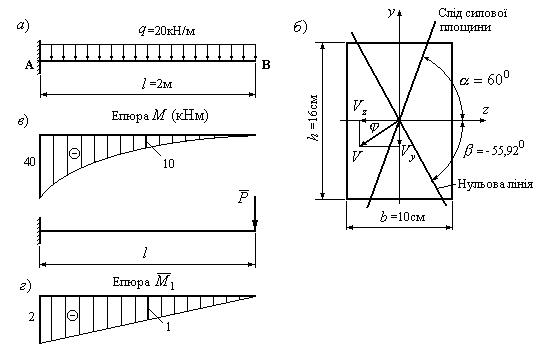
Рис.12.14

2. Застосовуючи метод МораСімпсона, помножимо вантажну епюру згинальних моментів на одиничну епюру згинальних моментів, використовуючи вирази (12.20) і (12.21):

ммм.

ммм.

Осьові моменти інерції перерізу см⁴ і см⁴ візьмемо з прикладу 12.1.

3. Визначаємо повний прогин перерізу В:

мм.

4. Напрям повного прогину знайдемо з виразу

.

Знайдені значення проекцій повного прогину і сам повний прогин відкладаємо на рисунку (Рис.12.14,б). Зважаючи не те, що проекції повного прогину вийшли при вирішенні задачі додатними, відкладаємо їх у напрямку дії одиничної сили, тобто униз () і вліво ().

5. Для перевірки правильності розв’язку задачі визначимо кут нахилу нульової лінії до осі :

.

Складемо модулі кутів і:

.

Це означає, що повний прогин перпендикулярний нульовій лінії. Таким чином, задача розв’язана правильно.