2.5. Згинання з розтяганням (стисканням)

Згинання з розтяганням (стисканням) відноситься до видів складного опору першої групи. При цьому виді складного опору можуть виникнути п'ять внутрішніх силових факторів: поздовжня сила , поперечні силитаі згинальні моментиі. Якщо знехтувати впливом дотичних напружень на міцність бруса, з п'яти внутрішніх силових факторів залишаються три. Цей випадок складного опору був докладно розглянутий у розділі 12.2 даного посібника. Тому усі формули для нормальних напружень і умови міцності, отримані в розділі 12.2, можуть бути застосовані і до розглянутого виду складного опору. Слід зазначити, що при виникненні складного згинання з стисканням, брус повинен мати велику жорсткість, тобто не втрачати стійкості.

Розглянемо окремий випадок дії навантаження, при якому виникає згинання з розтяганням. Балка консольного типу (Рис.12.15,а) з прямокутним поперечним перерізом навантажена похилою силою , що лежить у вертикальній площині. Розкладемо силуне дві складові: горизонтальну складовуі вертикальну складову. Від вертикальної складової силивиникає згинальний момент(Рис.12.15,б), від горизонтальної складової сили поздовжня сила (Рис12.15,в). Згинальний момент. Згинальний моментзмінюється за лінійним законом, досягаючи максимального значення у затиснені (перерізі А), поздовжня сила додатна і стала за величиною на всій довжині балки.

Нормальні напруження у довільно обраній точці перерізу для окремого випадку, що розглядується, визначимо за формулою (12.2) при :

. (12.25)

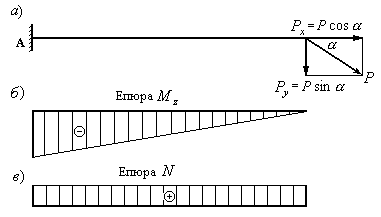
Рис.12.15

При визначенні напружень за формулою (12.25) застосовуємо спосіб простого додавання напружень від дії кожного з факторів окремо. На рис.12.16 наведений графічний приклад додавання напружень.

Рис.12.16

Рівняння нульової лінії одержимо, дорівнюючи нулю вираз для напружень:

, (12.26)

звідки знаходимо ординату нульової лінії

.

Максимальні напруження діють у волокнах, найбільш віддалених від нульової лінії. Умова міцності набуває вигляду:

. (12.27)

Умова міцності містить дві невідомі величини – осьовий момент опору і площу поперечного перерізу. У більшості випадків нормальні напруження від згинання більші, ніж від розтягання або стискання, тому при підборі перерізу можна спочатку не враховувати перший доданок і знайти наближене значення для моменту опору. Потім підбираються розміри поперечного перерізу по знайденій величині моменту опору. Розміри перерізу беруться трохи більшими проти необхідних і далі перевіряється міцність обраного перерізу за формулою (12.27).

12.6. Позацентрове розтягання (стискання) прямого бруса

Позацентрове розтягання (стискання) відноситься до видів складного опору першої групи. Цей вид деформації викликається силою, яка діє паралельно поздовжній осі стержня, але не проходить через центр ваги поперечного перерізу.

Розглянемо брус з довільною формою поперечного перерізу, який зазнає дії сили , паралельної осі бруса і перетинаючої поперечний переріз у точці А. Координати цієї точки в системі головних осей інерції перерізу позначимота(Рис.12.17). Відстань точки А від центра ваги перерізу позначимо буквоюі назвемо ексцентриситетом прикладення сили.

Прикладемо в точках В и 0 дві пари врівноважених систем сил. В результаті одержимо дві пари сил: і. Крім того в точці 0 залишиться сила, що діє уздовж осі. Ці зовнішні сили викликають у довільному поперечному перерізі, що розташований на відстанівід основи фігури, внутрішні силові фактори:;;.

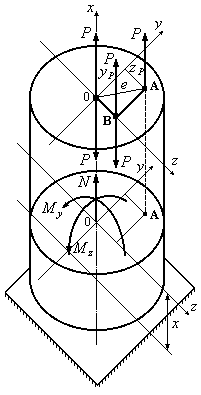
Рис.12.17

Таким чином, напруження у довільній точці поперечного перерізу будуть складатися з напружень, викликаних поздовжньою силою, і напруженнями чистого згинання, викликаного моментамиі. Розрахунок цих напружень виконаємо за допомогою формули (12.2). Після нескладних операцій цю формулу можна перетворити до вигляду (12.28), якщо виразити внутрішні зусилля через зовнішню силу:

. (12.28)

Беручи до уваги, що ; квадрати радіусів інерції перерізу відносно головних осей і, формулу (12.28) перетворимо до вигляду:

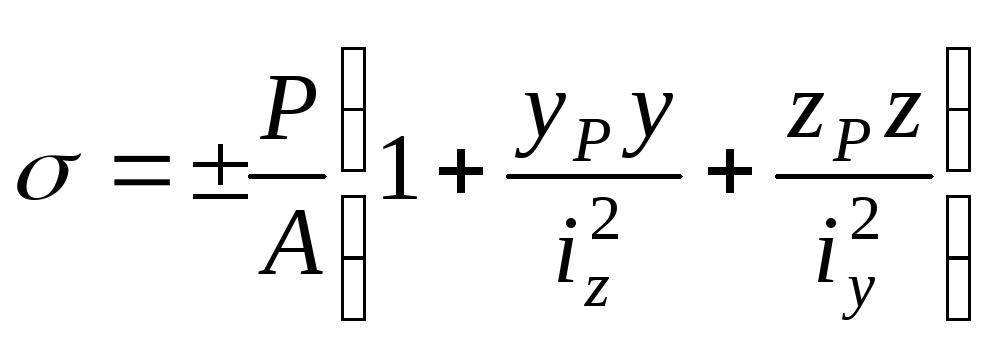. (12.29)

При визначенні напружень за формулою (12.29) знак “+” приймається для випадку, якщо сила розтягує. При стискальній силіперед дужкою у формулі (12.29) береться знак “”.

Оскільки при позацетровому розтяганні або стисканні виникає осьове розтягання (стискання) і чисте просторове згинання, усі поперечні перерізи стержня в однаковому ступені небезпечні. Небезпечну точку в поперечному перерізі знайдемо, побудувавши нульову лінію. Рівняння нульової лінії одержимо, дорівнюючи нулю напруження, обчислені за формулою (12.29) у довільній точці нульової лінії з координатами і:

. (12.30)

Побудуємо нульову лінію.

Зважаючи на те, що координати нульової лінії івходять у формулу (12.30) у першому ступені, нульова лінія є прямою лінією. Отже, її можна побудувати, визначивши відрізки, які нульова лінія відтинає на осях координат черезі. Для їх визначення задамо у формулі (12.30) значення. Тоді, позначивши відрізок, який нульова лінія буде відтинати на осічерезі вводячи його у формулу (2.30) замість, одержимо:

. (12.31)

Задаючи , аналогічним чином з формули (12.30) одержимо:

. (12.32)

Відкладаємо знайдені відрізки на осях координат (Рис.12.18) і будуємо нульову лінію.

Рис.12.18

Проаналізуємо поведінку нульової лінії при позацентровому розтяганні (стисканні):

 нульова лінія – пряма лінія;

 нульова лінія не проходить через центр ваги поперечного перерізу;

 нульова лінія проходить через дві чверті координат, ні однієї з яких не належить точка прикладення сили (нульова лінія ніколи не проходить через ту чверть координат, у якій знаходиться точка прикладення сили).

Тепер, маючи нульову лінію, проводимо паралельно їй дотичні до контура перерізу і знаходимо найбільш напружені волокна В і С у розтягнутій і стиснутій зонах перерізу (Рис.12.18). Напруження в цих волокнах (точках В і С) і умови міцності мають вигляд:

; (12.33)

. (12.34)

Координати точок прикладення сили і, а також координати точок А і В, у яких визначаються напруження, проставляються у формулах (12.33) і (12.34) зі своїми знаками. Епюра нормальних напруженьдля розглянутого випадку позацентрового розтягання наведена на рис.12.18.

Для прямокутного перерізу максимальні напруження виникають в одній з кутових точок і умову міцності зручно використовувати у такому вигляді:

. (12.35)

Вище був розглянутий випадок позацентрового розтягання. Отримані формули (12.33)(12.35) справедливі і для випадку позацентрового стискання за умови, якщо немає небезпеки виникнення втрати стійкості стержня.

Розглянемо кілька прикладів вирішення задач при позацентровому розтягання та стисканні.

Приклад 12.6. Стержень прямокутного профілю в точці А зазнає дії розтягальної сили кН (Рис.12.19). Визначити найбільші нормальні напруження в перерізі стержня.

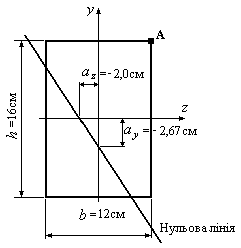
Рис.12.19

Розв’язок:

1. Визначаємо моменти інерції і квадрати радіусів інерції перерізу відносно головних осей і :

см⁴; см⁴;

см²; см².

2. Визначаємо відрізки, які нульова лінія відсікає на осях координат:

см; см.

3. Будуємо нульову лінію (Рис.12.19).

4. Найбільш віддаленою від нульової лінії є точка А. Напруження в цій точці буде найбільшим:

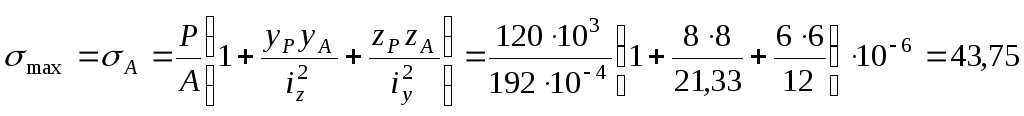МПа.

Приклад 12.7.У точках А двох колон прикладені стискальні сили (Рис.12.20). При цьому в точці С обох колон стискальні напруження виявилися однаковими. Порівняти напруження в точках В обох колон.

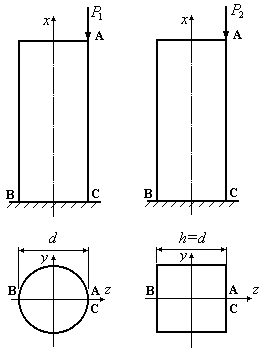
Рис.12.20

Розв’язок:

1. Позначимо висоту другої колони буквою і, з огляду на те, що для другої колони розмір, обчислимо для кожної з колон квадрати радіусів інерції перерізів відносно осі.

Для першої (лівої) колони:

;

Для другої (правої) колони:

.

2. Визначаємо напруження в точці С для першої колони:

. (а)

3. Визначаємо напруження в точці С для другої колони:

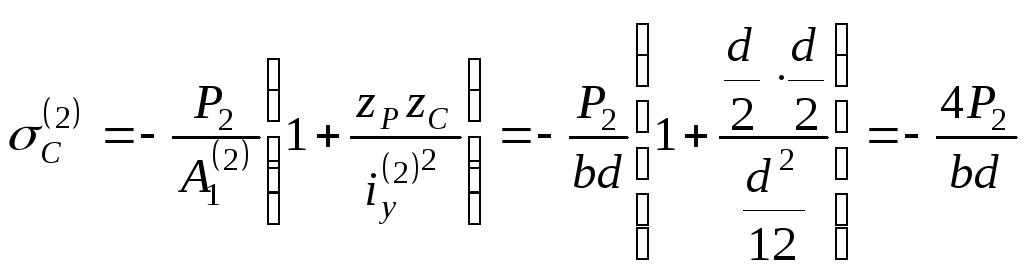. (б)

4. За умовою задачі нормальні напруження в точці С для обох колон однакові, тобто . Дорівнюючи вирази (а) і (б), виражаємо силучерез силу:

. (в)

5. Обчислюємо нормальні напруження в точці В перерізу для першої колони:

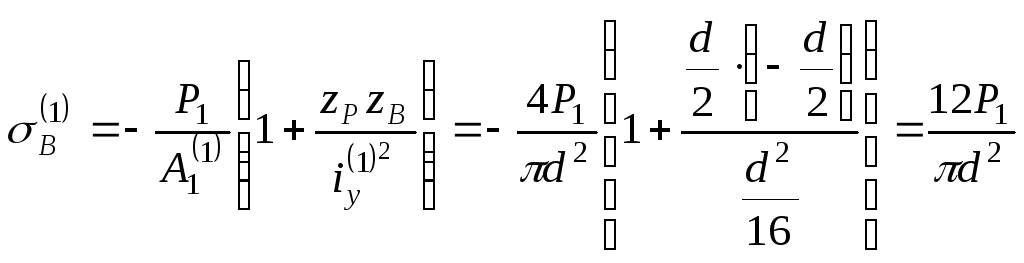. (г)

5. Обчислюємо нормальні напруження в точці В перерізу для другої колони:

. (д)

6. Напруження . Складемо їх співвідношення:

.

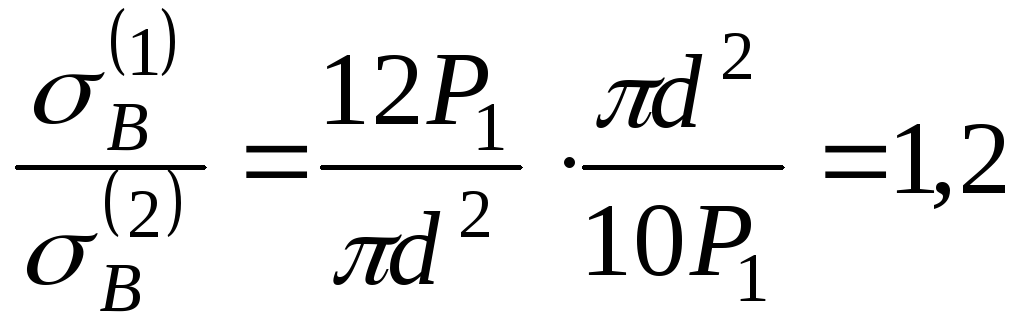Таким чином, напруження в першій колоні на 20% вище, ніж у другій.

Приклад 12.8.У точках А і В колони прямокутного перерізу прикладені однакові сили (Рис.12.21,а). Як зміниться найбільше стискальне напруження в колоні, якщо одну з сил забрати?

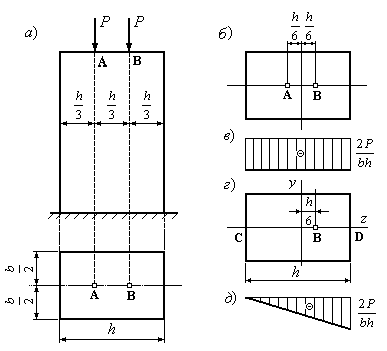
Рис.12.21

Розв’язок:

1. Знайдемо напруження в колоні, коли діють дві симетрично розташовані сили (Рис.12.21,б). Таке прикладення сил є центральним. У цьому випадку нормальні напруження від стискання знайдемо за формулою:

. (а)

У кожній точці поперечного перерізу напруження однакові. Епюра нормальних напружень наведена на рис.12.21,в.

2. Заберемо одну з стискальних сил, наприклад, силу, що діє в точці А. Сила, , що залишилася в точці В перерізу, спричинює позацентрове стискання. Встановимо небезпечні точки перерізу. З цією метою побудуємо нульову лінію. Рівняння нульової лінії має вигляд:

.

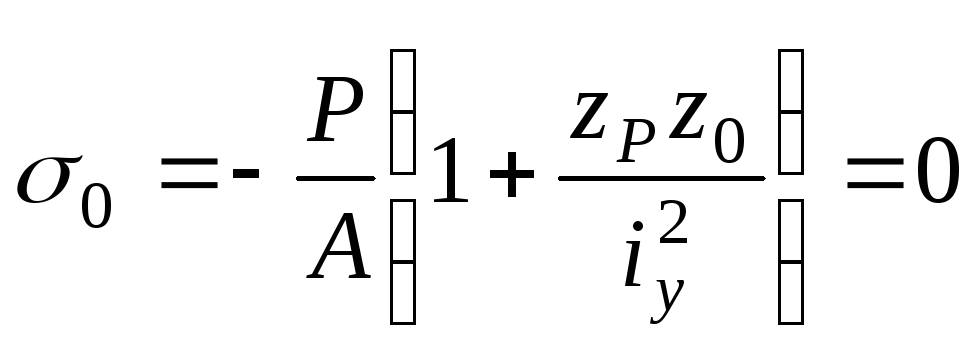Вирішуючи це рівняння відносно , одержимо:

.

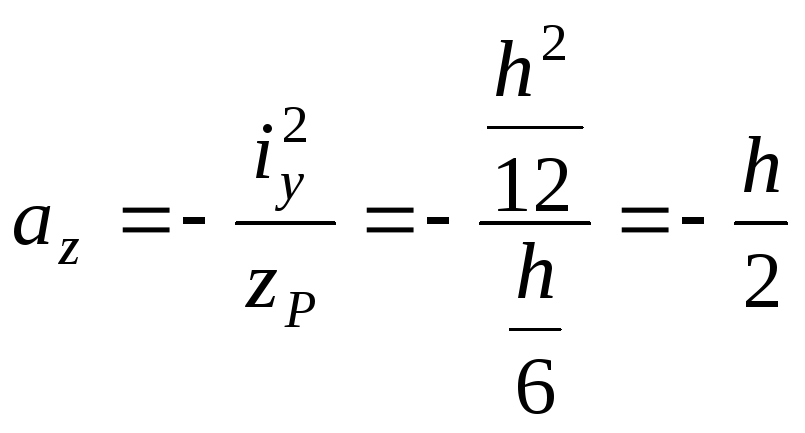Нульова лінія збігається з лівою крайкою перерізу. Напруження в точці С, що належить цій крайці, дорівнює нулю. Найбільше стискальне напруження виникне у точці D правої крайки перерізу. Обчислимо ці напруження:

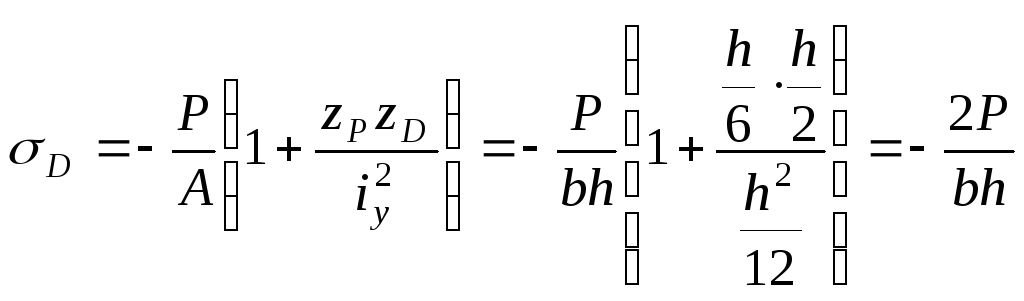. (б)

На рис.12.21,д наведена епюра розподілу нормальних напружень по площі перерізу. Максимальне за величиною напруження виникає у точці D перерізу.

3. Порівнюючи напруження в точці D з напруженнями, які були викликані двома однаковими симетрично розташованими силами (а), дістаємо висновку, що на питання, чи зміниться найбільше стискальне напруження в колоні, якщо одну з сил забрати, можна відповісти, що найбільше нормальне стискальне напруження в перерізіне зміниться.